三角函數探索題的類型及其解法
☉江蘇省宿遷青華中學 楊 兵
三角函數問題中的探索題,是指命題中缺少一定的條件或未給出明確的結論,需要經過推斷、補充并加以證明的問題.由于這類問題的知識覆蓋面大,綜合性強,方法靈活,再加上題意新穎,要求學生具有扎實的基礎知識和較高的數學能力,從而使三角函數探索題成為各種考試的一種常見題型.
一、條件探索題
條件探索題,即給出問題的結論,但沒有給出題目的條件,要求給出或補充使問題結論成立的條件.解這類題采取的策略是執果索因,首先要從結論出發,考慮結論成立時所要滿足的條件,再結合圖形及其性質逆向推導,尋找出所求條件.
分析:把條件①變形,判斷是否成立,然后根據化簡的結果,修改條件.
解:先判斷條件①是否成立.


說明:條件探索題涉及的知識較多,綜合性強,且是“逆向思維”,解此類問題需要有扎實的基本功及靈活處理問題的能力.
二、結論探索型
結論探索題的基本特征是給出條件而無結論或結論的正確與否需要確定.解此類題通常先假設其結論存在,再進行計算、推理,如果推導出符合條件的結論,則表示結論存在;若推出矛盾的結果,則結論不存在.


說明:本題要求找到三個數的關系,并說明理由,對思維能力要求較高,突出了對探索、歸納、推理能力的考查.
三、規律探索型
規律探索題的基本特征是給出若干圖形及圖形的變化規律等,需探索發現有關對象所具有的規律性或不變性的結論.通過觀察、歸納、類比、分析等思維方法,概括出一般規律或結論,然后再給出證明.
例3 設n∈N*,且sin x+cos x=-1,能否求出sinnx+cosnx的值?
分析:本題是與正整數有關的命題,可以先用不完全歸納法探索結果,然后用數學歸納法證明.

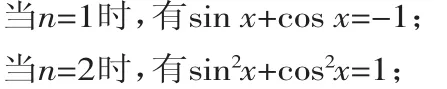
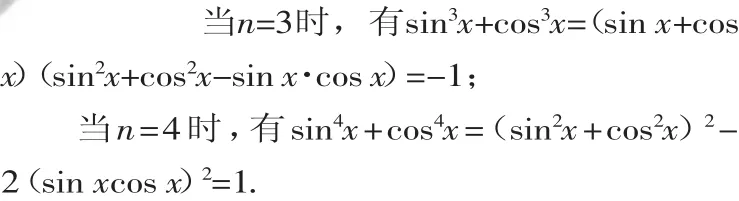
由此可以猜想當n∈N*時,sinnx+cosnx=(-1)n.
下面用數學歸納法證明.
(1)當n=1時,有sin x+cos x=-1成立.
(2)假設當n=k時,猜想成立,即sinkx+coskx=(-1)k.當n=k+1時,有sink+1x+cosk+1x=(sin x+cos x)(sinkx+coskx)-sin xcoskx-cos xsinkx=(-1)(-1)k-sin x·cos x(sink-1x+cosk-1x)=(-1)k+1.猜想成立.
由(1)(2)可知,當n∈N*時,sinnx+cosnx=(-1)n.
說明:對于解規律探索題,要合理利用題目中提供的信息,正確審題、分析、歸納,然后探索出結果.
四、存在探索型
存在探索題一般是在確定的條件下判斷某個數學對象是否存在.解決這類問題的策略是先假設需要探索的對象存在,從條件和假設出發進行運算、推理,若出現矛盾,則否定存在;如果不出現矛盾,則肯定存在.

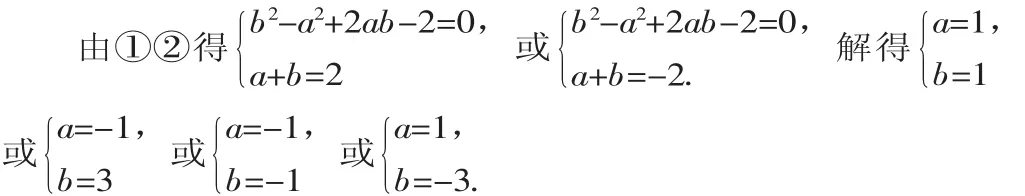
分析:可以將函數化為關于一個角的三角函數,再利用條件列出方程組求a、b的值.
所以存在a、b∈R,使本題結果成立.
說明:此題采用的方法是:觀察函數表達式的特征——假設存在——演繹推理——得出結論.
三角函數問題的探索題涉及的數學知識較多,解題過程較復雜,技巧性強,沒有現成的解題套路,因此 ,要求我們合情合理地分析,把直覺發現與邏輯推理相結合,更應該注重數學思想方法的綜合運用.

