他山之石 可以攻玉
☉江蘇省南京金陵中學河西分校 李玉榮
勾股定理形式簡單、寓意深刻,是人類的寶貴財富.關于勾股數,人們有如下的發現:
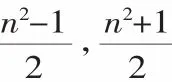
例1AB是⊙O的直徑,點E是半圓上一動點(點E與點A、B都不重合),點C是BE延長線上的一點,且CD⊥AB,垂足為D,CD與AE交于點H,點H與點A不重合.
(1)求證:△AHD∽△CBD
(2)連HB,若CD=AB=2,求HD+HO

解:(1)略;
(2)設OD=x,則BD=1-x,AD=1+x.
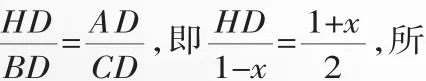
在Rt△HOD中,由勾股定理得:
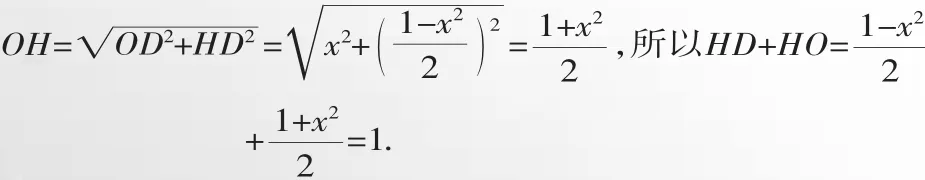
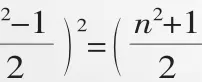
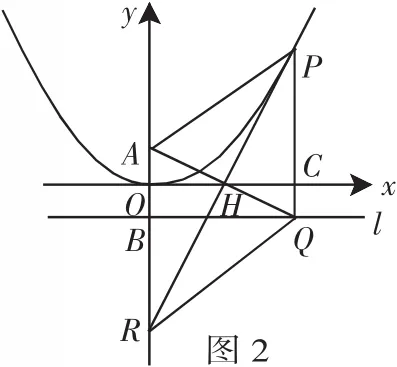
例2 探索研究:
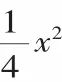
(1)求證:H點為線段AQ的中點;
(2)求證:①四邊形APQR為平行四邊形;②平行四邊形APQR為菱形;
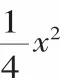
解:(1)、(2)①略;
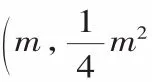
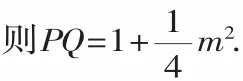
過P作PG⊥y軸,垂足為G,在Rt△APG中,AP=
所以平行四邊形APQR為菱形.
(3)略.
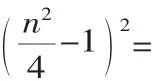
例3(2010年江蘇南通卷)已知拋物線y=ax2+bx+c經過A(-4,3)、B(2,0)兩點,當x=3和x=-3時,這條拋物線上對應點的縱坐標相等.經過點C(0,-2)的直線l與x軸平行,O為坐標原點.
(1)求直線AB和這條拋物線的解析式;
(2)以A為圓心,AO為半徑的圓記為⊙A,判斷直線l與⊙A的位置關系,并說明理由;
(3)設直線AB上的點D的橫坐標為-1,P(m,n)是拋物線y=ax2+bx+c上的動點,當△PDO的周長最小時,求四邊形CODP的面積.
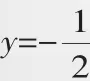
(2)相切;
(3)如圖3,過點P作PH⊥l,垂足為H,延長HP交x軸于點G.
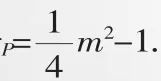
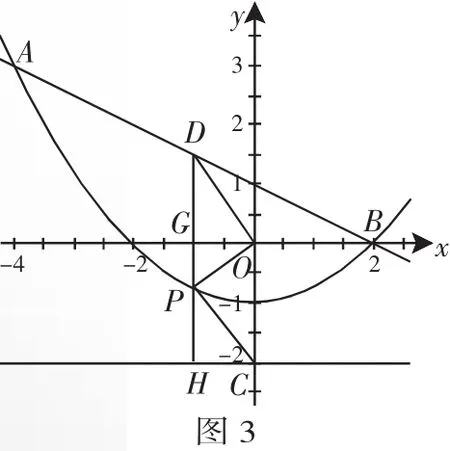
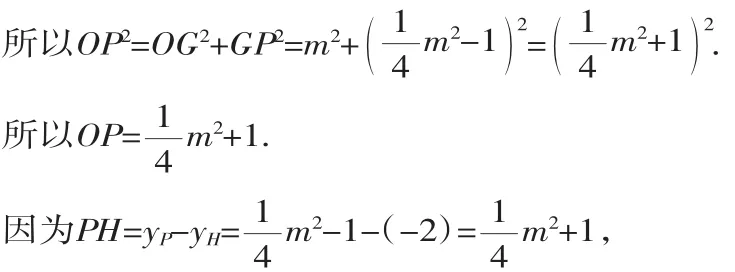
所以OP=PH,要使△PDO的周長最小,因為OD是定值,所以只要OP+PD最小.
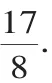
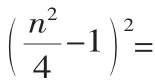
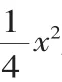
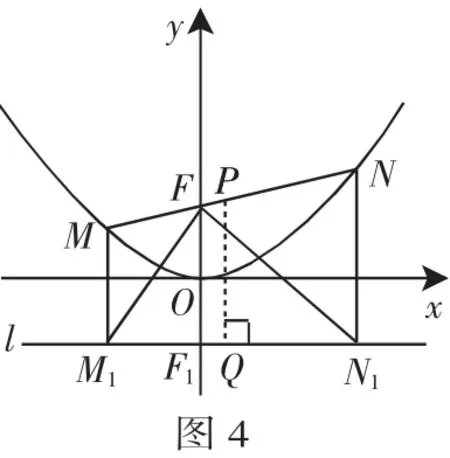
(1)求b的值.
(2)求x1·x2的值.
(3)分別過M、N作直線l:y=-1的垂線,垂足分別是M1、N1,判斷△M1FN1的形狀,并證明你的結論.
(4)對于過點F的任意直線MN,是否存在一條定直線m,使m與以MN為直徑的圓相切.如果有,請求出這條直線m的解析式;如果沒有,請說明理由.
解:(1)b=1;(2)、(3)略;
(4)存在,該直線為y=-1.理由如下:
直線y=-1即為直線M1N1.
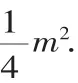
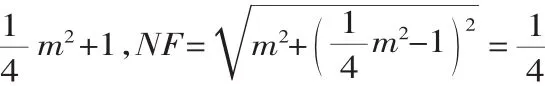

通過以上例題的分析,我們發現:只要選擇恰當的解決問題的方法,看似困難的問題往往并不像看上去那么困難,我們似乎得出這樣的結論:因為世上很多道理都是相通的,所以只要我們用心去發現,智慧就在我們身邊.

