運用winplot軟件輔助含參函數教學的案例解析

☉湖北大學數學與計算機科學學院 朱 慧

含參函數問題一直是高中教學中的難點，它融合數學知識以及多種數學思想方法，如數形結合、化歸、分類討論等，同時能很好地培養學生分析問題、解決問題的能力，因此備受命題專家、教師的青睞.然而對于學生而言，遇到含參函數就發懵，所以如何提高含參函數問題的解題能力一直是學生和老師所密切關注的事情.筆者經過嘗試，覺得適當運用winplot輔助教學，可以幫助學生直觀地理解知識、建構知識，提高解題能力.下面筆者主要結合自由軟件winplot的操作對含參函數的相關問題進行討論分析，與同仁們分享.

一、交點問題——觀察分析

例1 （改編于2011年陜西文科6）方程lgx=cosx在（-∞，+∞）內有_____個根？

分析 這是典型的數形結合的題目，一般只要畫出圖形就能解決.求根的個數實際上是求y=lgx與y=cosx的交點的個數.因為－1≤cosx≤1，lg1=0，而1rad≈57o，產生交點需lgx>0，所以交點只可能在（0，10）內，畫出圖形即可知為3個根.

但是如果將題目換種表述，例如：“要使lgx=cosax在（-∞，+∞）內有3個根（或者5個等等），則整數a為多少（或者求實數a的取值范圍）？”很多學生卻很盲目.顯然學生沒有掌握系數a與方程根個數之間的聯系.現在讓我們利用winplot的操作來對這方面問題進行探討.

具體操作如下：

步驟1：作（含參）函數圖像.單擊【window】/【2-dim】，在“noname 1”菜單欄中單擊【Equa】/【1.Explicit】，在“y=f（x）”圖形對話框輸入“log（10，x）”，點擊【lockinterval】填入lowx=0，highx=10，鎖定區間為（0，10）.點擊【ok】即可得到函數y=lgx的圖像.同理，輸入“cos（ax）”即得到含參函數y=cosax的圖像.（此時圖像為一直線，因為軟件默認參數初始值為0）

步驟2：改變參數值.在“noname1”菜單欄中單擊【Anim】/【Parameter A-W】得到“currentvalue of A”對話框，選擇參數a（代表參數的字母是不分大小寫的），按橫拉條左右拉動.如圖1使得y=cosax隨參數變化的動態圖像直接呈現在學生面前，抽出繁瑣的畫圖時間，讓學生可以充分地內化思考.

圖1

不難發現，當a增大時，y=cosax越來越密，與y=lgx的交點的個數越來越多.因此引導學生觀察后猜想，交點的個數與y=cosax有怎樣的聯系.結合a的意義，不難發現實際上交點個數是與y=cosax的周期緊密聯系，一個周期內如果有交點，最多有兩個.因此要使方程有三個根，則，即可求出整數a.

將winplot軟件用于數學課堂習題教學中，可以快速生動地呈現數學圖形，方便教師的教學，同樣，學生通過直觀的圖形更能很好地理解題目，積極地思考.

例2 已知二次函數y=ax2+bx+c和一次函數若它們的圖像對于任意的實數k都只有一個公共點，則二次函數的解析式為______.

分析 由于二次函數與一次函數的圖像只有一個公共點，則可以聯立方程知Δ=0.

由于方程（1）對任意的實數k都成立，即a=1，b=－2，c=1，y=x2－2x+1.

這道題雖然做完了，但筆者仍感覺不可思議（相信很多學生都會有這種疑惑）：“為什么會出現這種情況：給定拋物線解析式，居然存在一個含參量一次函數，不管參數如何變化，它們都有且只有一個交點.”自由軟件winplot可以幫我們揭曉秘密，具體操作同例1.

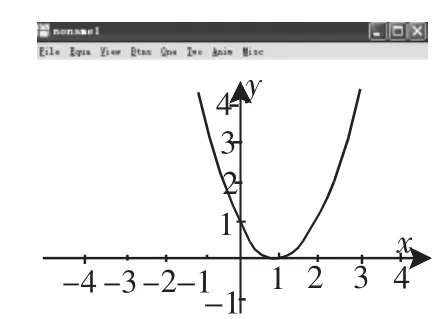
圖2

因此在教學時可以適當根據以上內容組織教學，讓學生經歷觀察，分析，進而聯系所學知識，猜想驗證，對題目知其所以然，并適當地總結，反思，學會舉一反三.

二、單調性問題——猜想驗證

分析 這類函數叫“對勾函數”，此題是人教版高中必修1教科書中第35面例5（3）題的引申.我們知道當a=1時，即在定義域內是奇函數，那么它的單調性如何呢？若a≠1時，它的奇偶性、單調性又如何呢？這是教師經常在課堂上拓展的.奇偶性很容易判別，這里不贅述.要想探索出單調性，就必須討論參量a的情況.而參量a的臨界值有哪些？很難找出，于是很多老師在這里只把對勾函數的性質當做結論直接灌輸到學生頭腦中，可想而知，學生沒有經歷體驗數學事實的過程，以至于到后來總把對勾函數與雙曲線混為一談.這里筆者借助winplot將探究過程一一展現.

步驟1：作含參函數圖像.參看例1步驟1.

步驟2：在“noname1”菜單欄中單擊【Anim】/【Parameter AW】，在得到的“currentvalue of a”對話框中選出參數a，點中橫拉條使其a=1（即a=1），即得到的圖像.

（1）作定點.單擊【Equa】/【Point】/【（x，y）】，在彈出的對話框中輸入x=“sqrt（a）”，y=“2sqrt（a）”，單擊【solid】/【ok】，在“naname1”中出現點（

圖3

（2） 作函數圖像上的動點.在“noname1”菜單欄中單擊【One】/【slider】在彈出的對話框中選中【makepoint】，會看到圖像中多了一個十字形（即動點）.拖動橫拉條，則十字形即動點在圖形上滑動，并且“slider”對話框中也會出現動點的坐標值.如圖3.

（3）作直線.單擊【Equa】/【Line…】，在彈出的對話框中依次輸入1，-1，0，即可得到直線x-y=0.

在不斷拖動“slider”對話框的橫拉條時，觀察x和y的坐標值，可以判斷當a=1時，的極值點.那么當a≠1時，又會是怎樣的呢？

小米通過互聯網實現了在線直銷產品，完全依托小米網站，舍棄了傳統手機銷售依靠線下出售的方式，這樣的最大好處就是去掉了層層代理環節，省下了大量銷售費用，既降低了小米手機的成本，同時又支撐起了小米采取的低價格、高性價比策略。

仿照例1中的步驟2，拖動橫拉條改變參數a的值，將圖像的變化演示出來.讓學生們觀察，并猜想當參量a變化時，函數的圖像性質如何？并且，教師可以根據學生的猜想有選擇的驗證，最終得出理想結論.例如當a<0時，圖像為上圖4（3），可知，在每個區間里都是增函數；當a=0時，圖像為一直線；當a>0時，圖像為對勾型.當然有條件的可以嘗試讓學生證明.

例4若函數f（x）=a|x-b|+2在［0，+∞）上為增函數，求實數a，b取值范圍.

分析 這是絕對值問題，初看一眼覺得無從下筆.仔細分析，要求a，b取值范圍，只告訴我們函數在［0，+∞）上為增函數，因此，必須弄清a，b對函數的影響.

步驟1：作含參函數圖像.參看例1步驟1.

步驟2：改變參數值.在“noname1”菜單欄中單擊【Anim】/【Parameter A-W】得到“currentvalue of A”對話框，選出參數a，任意確定一非零值.選出參數b，拖動橫拉條，觀察圖像隨b的變化情況.如圖5.同樣選出參數b，任意確定一非零值.選出參數a，拖動橫拉條，觀察圖像隨a的變化情況.如圖6.

不難發現：b正是函數圖像的彎折點，水平變化；a是函數的開口方向，a>0時，開口向上，a<0時，開口向下，當a=0時，函數為一條直線.所以很快就可以得出a>0，b≤0.

圖6

運用winplot繪圖軟件來輔助教學，將生澀的知識活靈活現地呈現出來，讓學生通過觀察、歸納、猜想、證明，形成自己的數學認知體系.

三、變換——對比歸納

例5 （必修4第1.5節）探索A、ω、φ對y=Asin（ωx+φ）的圖像的影響.

分析 多變量變化，我們采用控制變量法.要探究A、ω、φ對y=Asin（ωx+φ）的圖像的影響，就必須通過圖形的對比分析，歸納總結出規律.這里我們只談論A對y=Asin（ωx+φ）的影響.具體操作如下：

步驟1：作含參函數圖像.參看例1步驟1作出函數y=asin（bx+c）的圖像.

步驟2：探究a對函數圖像的影響.只需任意確定b與c的值，變化a的值來觀察圖像的變化情況.在“noname1”菜單欄中單擊【Anim】/【Parameter A-W】，在得到的“currentvalue of a”對話框中選出參數b，拖動橫拉條使其b=1（即b=1）；再選出參數c，拖動橫拉條使其c=0（即c=0），再選出參數a，左右拖動橫拉條，讓學生觀察并總結圖像隨著a的變化而變化的特征（紅色為y=sinx）.如圖7.

引導學生觀察，不難得出以下結論：當a>0時，y隨著a的增大而增大，相當于把y=sin（bx+c）的所有點的縱坐標伸長（a>1）或縮短（0

四、求含參量函數表達式——綜合運用

例6 在直角坐標系中，有以A（-1，1），B（1，-1），C（1，1），D（-1，1）為頂點的正方形，設它在y=|x－a|+a上側部分的面積為S（a），試求S（a）的解析式，并畫出y=S（a）的圖像.

分析 此題是人教版高中必修1教科書中第113面2題的引申.解決此類題型必須結合圖形來分析，找出函數S（a）關于a的分段點.然而y=|x－a|+a是一個絕對值表達式，很多學生得到y=后，不知如何找出S（a）關于a的分段點.因此，首先要找到y=|x－a|+a的圖像特征，通過觀察找出S（a）的分段點.利用winplot中參數值的可變性，可以很快發現y=|x－a|+a的關于a的變化情況.具體操作如下：

步驟1：作定點.仿照例2步驟2中的（1）依次作出點A（-1，1），B（1，-1），C（1，1），D（-1，1）.仿照例2步驟2中的（2）作出動點（a，a），此動點即為y=|x－a|+a的圖像的彎折點.

步驟2：作線段.單擊【Equa】/【Segment】，在彈出的對話框中（如圖8）依次輸入-1，1，-1，-1，單擊【ok】得到線段AD，如圖9.重復上述操作，即可得到正方形ABCD.

圖8 圖9

步驟3：作含參函數圖像.仿照例1步驟1.

步驟4：改變參數值.仿照例1步驟2，改變參數a的值.

不難發現：隨著a的變動，彎折點在直線y=x上移動.于是很容易得到a的分段點為1，0，-1.圖像如圖10.（讀者可以嘗試摸索陰影部分是如何做出來）

圖10

新課程標準中強調“高中數學課程應提倡實現信息技術與課程內容的有機整合，整合的基本原則是有利于學生認識數學的本質.高中數學課程應提倡利用信息技術來呈現以往教學中難以實現的課程內容……”.當然winplot的功能遠不止這些，例如迅速作出參數方程的的圖像、求函數的零點、極值、周期，對函數進行平移、旋轉、反射等等，還有高等數學中的相關應用.對于我們教師自主編題、快速解題、探究性教學等都很有幫助.但需要強調的是，winplot軟件只是作為教學的輔助工具，切不可泛濫使用，針對學生要打好基礎，重視數學知識與能力的培養，不可本末倒置、投機取巧.