經(jīng)典試題 魅力綻放——對(duì)一道高考題的多種求解策略

☉江蘇省丹陽(yáng)市第六中學(xué) 朱萬(wàn)喜（特級(jí)教師）

（1）求橢圓的方程；

（2）設(shè)A、B是橢圓上位于x軸上方的兩點(diǎn)，且直線AF1與直線BF2平行，AF2與BF1交于點(diǎn)P.

（ii）求證：PF1+PF2是定值.

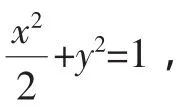
策略一：本題綜合考查了橢圓的定義、標(biāo)準(zhǔn)方程及幾何性質(zhì)、直線方程、兩點(diǎn)間距離公式等基礎(chǔ)知識(shí)，第二問(wèn)考查曲線與方程的關(guān)系.我們知道解析幾何的本質(zhì)是用代數(shù)方法研究幾何問(wèn)題，其核心思想是坐標(biāo)法思想，聯(lián)立方程組是“首當(dāng)其沖”的想法.

解法1：（2）由（1）知F1（－1，0），F(xiàn)2（1，0），又直線AF1與BF2平行，所以可設(shè)直線AF1的方程為x+1=my，直線BF2的方程為x－1=my.設(shè)A（x1，y1），B（x2，y2），y1>0，y2>0.

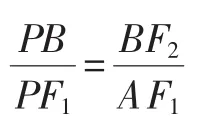
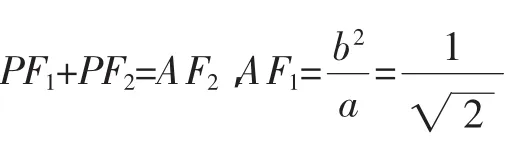
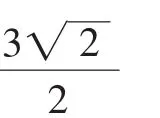
設(shè)A（x1，y1），B（x2，y2），直線AF1的方程為x+1=my，直線AF1與橢圓交于兩點(diǎn)，一點(diǎn)是A，記另一點(diǎn)B′（－x2，－y2）.

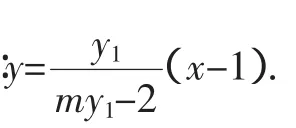
解法1是國(guó)標(biāo)答案，解法2做了一些改進(jìn)：其中第一小問(wèn)使用焦半徑公式；第二小問(wèn)筆者轉(zhuǎn)化為求P點(diǎn)軌跡問(wèn)題.這兩種解法雖然想法直接，但運(yùn)算繁瑣，過(guò)程冗長(zhǎng)，多數(shù)學(xué)生難以“忍受”.對(duì)于解析幾何問(wèn)題，學(xué)生多少會(huì)有一些思路，但結(jié)果常以失敗告終.根本原因是未能找到合理、便捷的將“幾何問(wèn)題代數(shù)化”的轉(zhuǎn)化途徑，導(dǎo)致“誤入歧途”，深陷煩瑣運(yùn)算的“泥潭”，筆者認(rèn)為對(duì)于解析幾何問(wèn)題還要還原“幾何”本源，從題中的幾何特征入手.

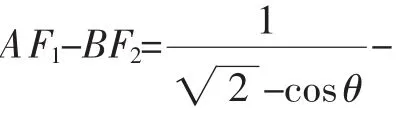
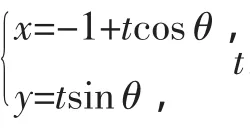
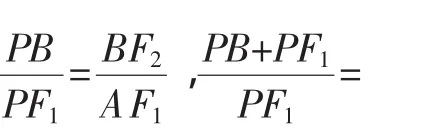
通過(guò)對(duì)解析幾何的復(fù)習(xí)，讓學(xué)生體驗(yàn)感悟數(shù)學(xué)知識(shí)之間的本質(zhì)聯(lián)系；拓展研究創(chuàng)新視野；培養(yǎng)綜合分析問(wèn)題及應(yīng)用數(shù)學(xué)知識(shí)解決問(wèn)題的能力，使解析幾何復(fù)習(xí)更有針對(duì)性，從而提高復(fù)習(xí)的效率，這樣才能在高考中立于不敗之地.■