數學探究教學根植教材的三個視角

洪麗敏

美國著名的未來學家阿爾福·托夫勒在《未來的沖擊》中一針見血地說：“21世紀的文盲不再是目不識丁的人，而是不會學習的人！”可見，教育倡導培養會探究、會學習的學生，教師的首要任務是要有所教、有所授。而教材是學生學、教師教的直接載體，也是進行數學探究教學的重要載體。本文以人教A版2-1為例，以圓錐曲線為切入口，談談挖掘教材、踐行探究的三個視角。

一、關注概念本質，螺旋上升

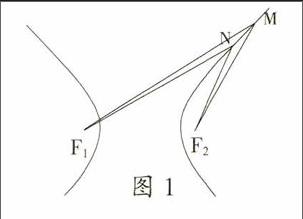
概念教學是解析幾何教學的基礎，也是一個難點。橢圓、雙曲線的定義緊扣的是“兩定點，一定值”，拋物線則是“一點一直線”，雖然教材在呈現它們定義時都采用“具體操作”直觀說明定義，但是，教師也不能忽視對直觀表面后的數學本質進行闡釋。如雙曲線中的“拉鏈”問題，教師要引導學生關注“拉鏈”變化中的“變與不變”，如圖1，當拉鏈由N處拉開到M處時，“變”的是|MF1|，|MF2|（|MF1|=|NF1|+|MN|，|MF2|=|NF2|+|MN|），“不變”的是|MF1|與|MF2|的差（|MF1|-|MF2|=|NF1|-|NF2|為定值），同時要引導學生體會其中隱含的“等量”的思想。

波利亞說過：“一個恰當的例題勝過一打理論。”這表明教師在引導學生建構數學概念的時候，如果能夠舉出一個既揭示數學概念本質又通俗易懂的例題，那么這個例題則勝過教師對概念“空對空”的很多遍重復解釋。教師使用恰當的例題，能夠降低其概念的抽象程度，突出概念的實質，有助于學生建構數學概念的意義[1]。三種圓錐曲線有很多方面可進行類比，因此，教師可通過題組變式探究的形式，讓學生辨認，揭示“形異”背后的“神同”，加深理解概念本質。

例1（第50頁B組第2題）一動圓P與圓O1：x2+y2+6x+5=0外切，同時與圓O2：x2+y2-6x-91=0內切，求動圓圓心P的軌跡方程，并說明它是什么曲線。

解：設動圓的半徑為R，則|O1P|=R+2，|O2P|=10-R，∴|O1P|+|O2P|=12

則動圓圓心P的軌跡是以O1，O2為焦點，長軸長為12的橢圓，軌跡方程為+=1。

我們可以改變兩圓的不同位置關系或半徑，觀察動圓圓心P的變化。

變式1：一動圓P與圓O1：（x+3）2+y2=4內切，同時與圓O2：（x-3）2+y2=100內切，求動圓圓心P的軌跡方程。

變式2：一動圓P與O1：（x+3）2+y2=9外切，同時與圓O2：（x-3）2+y2=1外切，求動圓圓心P的軌跡方程。

變式3：一動圓P過點A（3，0），且與直線l：x=-3相切，求動圓圓心P的軌跡方程。

通過三個變式，可以看到隨著兩圓的位置關系或半徑的不同，動圓圓心的軌跡也會隨之而“變”，但“不變”的是它們的處理方法，都是緊扣兩圓（或點圓）的位置關系，都圍繞著一個共同的主題——圓錐曲線的定義。

同時，雖然課程標準對圓錐曲線的統一定義已不做要求，但教材卻在例題上逐漸滲透，因此在章節復習時，教師可以引導部分學有余力的學生回顧、對比、總結。如第47頁例6（橢圓）、第59頁例5（雙曲線）、第76頁閱讀與思考“圓錐曲線的離心率與統一方程”。

這樣，通過如此的“螺旋上升”、“逐步深化”的探究，學生對三種圓錐曲線定義的理解也將日益加深，更清楚其定義背后的“定點、定值”的內涵。

二、挖掘例題習題，提升能力

教材中的例題都是典型的，具有一定的代表性，例題教學是決定教學效果的重要環節。教師可以從一個簡單例題出發，在不斷改變例題背景或條件的基礎上，展開討論，同時結合學生的學情（如學段、基礎等）最大限度地發掘一道例題的功能。

例2 （人教A版第80頁A組第11題）在拋物線y2=4x上求出一點P，使得點P到直線y=x+3的距離最短。

解：方法一：設直線l：x-y=t，聯立方程有x2-2（t+2）x+t2=0，由△=4（t+2）2-4t2=0得t=-1，則最短距離d==，此時把t=-1代入可求得P（1，2）。

方法二：設P（x，y），則有y2=4x。此時點P到直線y=x+3的距離 ? ?，故當P（1，2）時，最短距離為。

（1）縱橫聯系，比較異同

對比課本第47頁例7：已知橢圓+=1，直線l：4x-5y+40=0。橢圓上是否存在一點，它到直線l的距離最小？最小距離是多少？

評注：通過對比，可發現解決“求圓錐曲線上一點到已知直線的最短距離”的通性通法為“切線法”，即通過平移直線，使其與該圓錐曲線相切。不同的是，拋物線也常轉化為二次函數的最值問題，橢圓則常可借助參數解決。

（2）改變條件，辨認選擇

變式1：在拋物線y2=4x上求出一點P，使得點P與點A（-3，0）的距離最短。

解：方法一：|AP|==，所以當P（0，0）時，距離最短為3。

方法二：由圖2，考慮拋物線的對稱性，所以當P（0，0）時，距離最短為3。

評注：方法一是處理兩點間距離的一般的方法（即通性通法），而方法二則緊扣幾何特征，數形結合，小巧玲瓏。

（3）探索推廣，以點帶面

變式2：在拋物線y2=4x上求出一點P，使得點P與焦點F（1，0）的距離最短。

分析：受上述方法二的影響，學生易得當P（0，0）時，距離最短為1。

變式3：在拋物線y2=4x上求出一點P，使得點P與點A（a，0）的距離最短。

分析：受上述兩個問題的影響，多數學生認為當P（0，0）時，距離最短為|a|。事實果真如此嗎？

解：|AP|==，

當a-2<0即a<2時，取P（0，0）時，距離最短為3;

當a-2≥0即a≥2時，取P（a-2，±2）時，距離最短為2。

（4）改變背景，追本溯源

變式4：若拋物線y2=4x與動圓C：（x-a）2+y2=1沒有公共點，求實數a的取值范圍。

解：方法一：聯立方程有x2+（4-2a）x+a2-1=0，其在x∈[0，+∞）內沒有實數根，設

f（x）=x2+（4-2a）x+a2-1，則△≥0，-<0f（0）>0或△<0，解得a<-1或1<a≤或a>，綜上，實數a的取值范圍為（-∞，-1）∪（1，+∞）。

方法二：圓心C（a，0），半徑r=1，則|PC|==，

由條件結合圖3，可知|PC|min>r。

當a<2時，|PC|min=|a|>1，解得a<-1或a>1，故a<-1或1<a<2;

當a≥2時，|PC|min=2>1，解得a>故a≥2;

綜上，實數a的取值范圍為（-∞，1）∪（1+∞）。

評注：方法一利用坐標法，把幾何問題轉化為代數問題，屬解析幾何問題解決的通性通法，但應該看到其解題過程的代數處理相對復雜;方法二則緊扣解析幾何“形”的一面，把問題轉化為|PC|min>r。

（5）感悟高考，類比遷移

（2014高考福建卷第9題）設P，Q分別為x2+（y-6）2=2和橢圓+y2=1上的點，則P，Q兩點間的最大距離是（ ? ）

解：如圖4，問題轉化為求橢圓上的點Q到圓心C（0，6）的最大距離圓的半徑r=。設Q（x，y），則

從而P，Q的最大距離為 ? ?，故選D。

評注：解析幾何的核心思想是坐標法，但是，解析幾何首先有幾何“形”的一面，數形結合同樣是解析幾何的一個重要思想。因此，在教學上教師要培養學生良好的解題習慣：條件圖形化（即準確畫出曲線圖形）;條件、結論代數化（即對條件、結論的幾何特征分析，把幾何特征用代數表示）;條件、結論融合化（即尋求合適的計算途徑，用代數方法解決幾何問題）。可見，圓錐曲線問題的解決常利用“形”轉化，再用“數”解決。

三、重視閱讀材料，拓寬視野

高中數學教科書開辟了“閱讀與思考”“探究與發現”“信息技術應用”等拓展性欄目。其內容或是滲透數學文化，弘揚數學精神;或是延伸教材內容，完善知識體系;或是聯系生活實踐，開拓學生視野……教師應當正確認識到教材中閱讀材料的地位和作用，挖掘其深層次內涵，發揮其應有的教育教學功能[2]。

例3 （選修2-1第43頁“探究與發現”——為什么截口曲線是橢圓）如圖5，雖從幾何直觀上告訴我們用一個平面去截圓錐，得到的截口曲線是橢圓。但是其原因對多數學生來說有一定的挑戰性。教學中教師要注重其原理的揭示（類比圓得到球的切線性質AB=AF，AC=AE，∴AE+AF=AB+AC=BC），同時要提供機會讓學生操作，如圖6，“用一個與圓柱的母線斜交的平面截圓柱，得到一條截口曲線，你能仿照上述方法，證明截口曲線也是橢圓嗎？”如圖7，類比圖5可得以證明。

同時，借助圖7，讓學生明白，切點E，F恰為橢圓的焦點，底面圓恰為橢圓在底面上的投影，因此橢圓的短軸長恰為底面圓直徑2r，設橢圓面與底面所成角為？琢，則橢圓長軸長2a=，進一步揭示了橢圓與圓的關系。

為了加深理解，教師可以設置相應題目加以強化。比如：（2011年高考湖北理14）如圖8，直角坐標系xoy所在的平面為？琢，直角坐標系x′oy′（其中y′軸與y軸重合）所在的平面為？茁，∠xox′=45°。

（Ⅰ）已知平面內有一點P′（2，2），則P′點在平面？琢內的射影C的坐標為_____;

（Ⅱ）已知平面？茁內的曲線C′的方程是（x′-）2+2y'2-2=0，則曲線C′在平面？琢內的射影C的方程是_______。

有效教學提倡“用教材”而不是“教教材”。“用教材”要求教師把教材當作素材，根據實際情況對教材進行靈活的調整、重組、拓展而后組織教學，“用教材”是基于教材而又不拘于教材的一種教學主張。

數學探究教學作為一種有效的教學模式，只有根植于教材的開發，才可以煥發生命力，才能真正提高教學效率。

參考文獻

[1] 沈威，涂榮豹.探悉數學例題教學的規律[J].教學與管理，2009（7）.

[2] 楊蒼洲，林少安.基于教材的教學延伸策略[J].數學通訊，2014（8）.

【責任編輯 ? 郭振玲】