以研立學 因?qū)W而教

周艷

[摘 要]“梯形的面積計算”是在學生已經(jīng)熟練掌握了長方形、正方形，尤其是平行四邊形和三角形的面積計算和梯形的認識的基礎上學習的數(shù)學問題。特級教師周衛(wèi)東教學此內(nèi)容時，沒有沿襲以往的教學思路，亦步亦趨地讓學生從“0”開始進行學習，而是立足于學生已有的數(shù)學知識和經(jīng)驗，以研立學，因?qū)W而教，通過引導點撥讓學生經(jīng)歷了自主研究與發(fā)現(xiàn)，最終獲得提升的學習過程，讓學生在再創(chuàng)造中自我建構(gòu)新知、解決問題。

[關(guān)鍵詞]自我建構(gòu) 數(shù)學思考 數(shù)學思想 數(shù)學活動經(jīng)驗

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2015）14-017

【片斷一】各小組交流如何計算梯形面積后匯報。

生1：我是這樣想的，兩個完全一樣的三角形可以拼成一個平行四邊形，那么兩個完全一樣的梯形也可以拼成一個平行四邊形，拼成的平行四邊形的底等于梯形的上底加下底，平行四邊形的高就是梯形的高，而梯形的面積就這個平行四邊形的一半，所以梯形的面積=（上底+下底）×高÷2。（方法1）

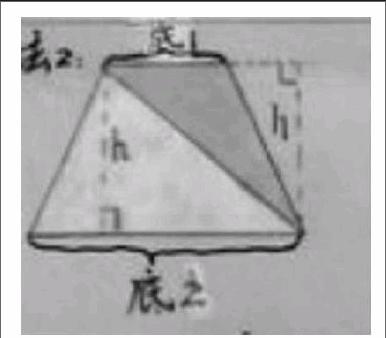
生2：我有不同的方法。把梯形分成兩個三角形，因為三角形的面積我們是會算的，梯形的面積=三角形1的面積+三角形2的面積，三角形1的面積就是（底1×高÷2），三角形2的面積就是（底2×高÷2），如圖1，底1就是梯形的上底，底2就是梯形的下底，梯形的高也就是三角形的高，所以梯形的面積就是“（梯形上底+梯形下底）×高÷2”。（方法2）

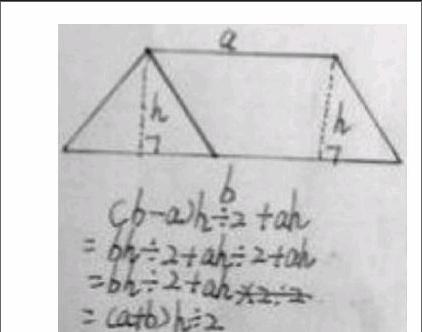
生3：還可以把梯形分成平行四邊形和三角形。平行四邊形的面積是底×高，三角形面積是底×高÷2，平行四邊形的底是梯形上底，三角形的底是（梯形下底-梯形上底）。那么平行四邊形的面積就是“梯形上底×高”，三角形面積是“（梯形下底-梯形上底）×高÷2”，把兩部分合起來就是“梯形上底×高+（梯形下底-梯形上底）×高÷2”，把這個算式整理一下就是“梯形下底×高÷2+梯形上底×高÷2”，也就是“（梯形上底+梯形下底）×高÷2”。（方法3）

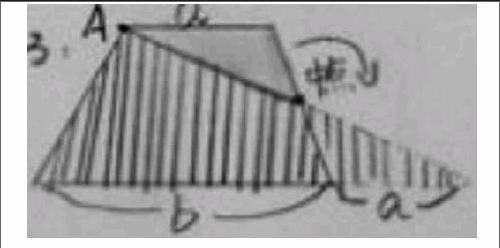
生4：我還有不同的方法。在梯形的腰上找到中點，連接A點和中點，將這個三角形旋轉(zhuǎn)，得到一個新的三角形，新三角形的面積和原來梯形面積相同，新三角形的面積是（底×高÷2），新三角形的底就是（梯形上底+梯形下底），所以梯形的面積就是（梯形上底+梯形下底）×高÷2。（方法4）

生5：我和生4的方法有一點類似，把梯形沿著腰的中點分割開，然后補成一個平行四邊形。這個拼成的平行四邊形的面積和原來梯形的面積是一樣的，平行四邊形的底就是梯形的上底加下底的和，平行四邊形的高是梯形的高的一半，平行四邊形的面積是（梯形上底+梯形下底）×（高÷2），所以梯形的面積也就是（梯形上底+梯形下底）×高÷2。（方法5）

生6：我想問為什么從中點切開，補成的這個圖形就是一個平行四邊形呢？

生7：我可以用一個梯形剪一下。（操作演示了從梯形中位線剪開拼成平行四邊形的過程）

師：生6的問題提得很好，說明他很善于思考，不過生7也很愛懂腦筋，能想到用一個梯形進行簡拼。生5的推理方法是正確的，但是以我們目前學習的方法還不能嚴格地證明這種推導方法，有興趣的同學課后可以再學習。

師：在這里，老師還有一個問題，在這些方法中都要除以2，為什么梯形的面積計算要除以2呢？

生8：因為用兩個完全一樣的梯形可以拼成平行四邊形。我們先算了平行四邊形的面積，因為平行四邊形是由兩個完全相同的梯形拼起來的，所以算梯形的面積當然要用平行四邊形的面積除以2了。

……

《禮記·學記》中記載：“獨學而無友，則孤陋而寡聞?！睂W習需要有獨立思考的過程，但更需要有合作交流的成分，課堂展示交流充分將學生的學習收獲分享于眾，展示交流為他們個性化的思考提供了巨大的空間，從而使學生獲得一種莫大的成就感。首先讓學生充分運用割補、平移和旋轉(zhuǎn)等策略，通過遷移轉(zhuǎn)化，溝通了平面圖形之間的內(nèi)在聯(lián)系，得出公式推導的多種方法，落腳點都是梯形的面積計算公式，最后，再將梯形面積計算公式中“除以2”的難點留給學生去解釋。整個教學過程中教師退居講臺之后，只在學生有疑難處適時出手，強調(diào)了重點，突破難點，真正落實了教學目標。

【片斷二】師：剛才同學們想出了不同的方法推導出了梯形的面積計算公式，非常了不起，反觀這幾種方法，你能找一找這些方法之間的相同和不同嗎？

生1：這些方法都是將梯形轉(zhuǎn)化成我們已經(jīng)學過的圖形來計算面積，然后推導出梯形面積計算的方法的。

生2：方法2和方法4是把梯形轉(zhuǎn)化成三角形來算的。

生3：方法1和方法5是把梯形轉(zhuǎn)化成平行四邊形來算的。

師：在轉(zhuǎn)化時用的方法上有什么類似的地方嗎？

生4：方法2、方法3是把梯形分割成我們學過的圖形來算的。

師：這兩種方法用到了分割的策略。（板書“分割”）

生5：方法4、方法5是把梯形剪開，然后再拼成新的圖形來算的。

師：這兩種方法用到了剪拼的策略。（板書“剪拼”）

師：這些方法都是將梯形轉(zhuǎn)化成我們學過的圖形進行計算的。

……

對于梯形面積計算公式的推導，多樣的方法并非教學目的，而是通過多種方法的展示，讓學生之間可以相互學習、相互啟發(fā)、開拓思路、啟迪智慧。教師在尊重學生主體地位的同時，還應該時刻記住自己的主導身份，適時點撥，揭示知識的數(shù)學實質(zhì)及體現(xiàn)的數(shù)學思想，幫助學生理清相關(guān)知識之間的聯(lián)系與區(qū)別。在這里，學生面對多種推導方法，到底要從這些方法中學到什么？這是我們教師需要心中有數(shù)的，因為具體的知識應用是十分有限的，解決問題的方法與策略才是更高層次的學習內(nèi)容，是我們所追求的教學目標。在面積推導中蘊含了豐富的轉(zhuǎn)化策略，和將未知轉(zhuǎn)化成已知的數(shù)學思想，教師通過適當?shù)奶釂?，引導學生再次反觀眾多方法，異中求同，提煉了“剪拼、分割”的轉(zhuǎn)化策略，使學生深刻體會到轉(zhuǎn)化的數(shù)學思想，為后續(xù)的相關(guān)學習積累了有效的數(shù)學活動經(jīng)驗。

【片斷三】學生在明確了梯形的面積計算公式后，已經(jīng)會運用梯形的面積計算公式進行簡單計算。周老師沒有就此打住，而是出示了一道變式題，將學生的思維引向深處。

生：46-20=26（米），26×20÷2=260（平方米）。

師：這里沒有給出梯形的上底和下底，你是怎么求的？

生：我們求梯形的面積時要知道上底和下底是為了知道上底和下底的和，在這里求出“46-20”就可以知道上底和下底的和了，所以就可以求梯形的面積了。

師：做了這道題，你有什么想法？

生：不要生搬硬套梯形的面積公式，有時候不知道上底和下底分別是多少也沒關(guān)系，關(guān)鍵是要知道梯形上底和下底的和。

……

學習是一種積累的過程，它不在于解決問題的某種小技巧，而是一種面對新問題勇于嘗試與探究的精神與勇氣，最重要的思想是讓大多數(shù)人能夠以他們可以接受的方式主動學習，讓所有人能從學習中獲得自信，和一份積極向上的精神狀態(tài)。學習“梯形面積的計算”這一內(nèi)容，直接套用梯形的面積公式進行計算，大部分學生都可以很熟練，然而，這樣的基礎練習容易讓學生產(chǎn)生思維定式，影響對梯形面積計算的靈活應用，而這道練習題的呈現(xiàn)，打破了學生原先的思考套路，讓他們在練習中自己發(fā)現(xiàn)計算梯形面積時并不是一定要知道梯形的上底和下底分別是多少，關(guān)鍵是要知道上底加下底的和，從而領會梯形面積計算的核心要義，真正實現(xiàn)了“讓人人都獲得良好的數(shù)學教育，不同的人在數(shù)學上得到不同的發(fā)展”課程目標要求。

（責編 金 鈴）