淺談超級畫板在初中數學中的應用

魏凌雪

【摘要】現代信息技術是數學課程中一種重要的課程資源。數學教學過程總恰當地使用信息技術將在很大程度上提高學生從事數學教學活動的水平和教師從事教學活動的質量。本文主要結合自身教學實踐，列舉了超級畫板在初中數學應用的幾個方面，供大家交流探討。

【關鍵詞】信息技術 ?超級畫板 ?初中數學

2011版《數學課程標準》提出：學生的數學學習的內容應當是現實的、有意義的、富有挑戰性的，而內容的呈現應采用不同的表達方式，以滿足學生多樣化的學習需求。《超級畫板》是一種適合數學教學的工具。它可以幫助學生在動態中去觀察、探索和發現對象之間的數量變化關系與結構關系，是一種新型有效的教學輔助工具，是加強傳統教學，優化教學過程，提高課堂教學效率的重要手段。在初中數學課堂教學中，運用超級畫板課件輔助教學，能激發和調動學生學習數學的積極性，從而較好地培養學生自主學習、探究問題的能力。下面就是我在教學過程中對超級畫板應用的一些嘗試與經驗與大家一同分享探討。

一、幾何方面：

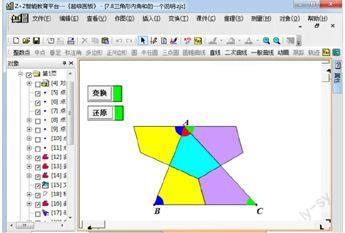
1、教學中我經常發現一些學生對軸對稱圖形和中心對稱圖形的概念非常熟悉，可是真正判斷的話還是有一定的困難，學生很難想象這個圖形翻折后或者旋轉180度之后是什么情況，于是老師讓學生把一些常見圖形是不是軸對稱圖形或者是不是中心對稱圖形背出來，我想這樣的做法不是最理想的，如果我們利用超級畫板，把一個圖形是怎樣沿著某一條直線翻折過來，然后直線兩旁的部分是怎樣重合或不重合的過程展示給學生看的話，效果很好，用同樣的手段展示旋轉的過程，這樣學生才能真正明白為什么是或者不是。

2、如學習“三角形三內角和為180度定理時，我們可以讓學生繪制一個三角形，測量出每個角的度數和三內角和的值，并拖動三角形的任一個頂點，觀察三個內角之和是否仍保持為180度。這樣在感性認識上首先建立起認知新知識的起點，為推理論證的順利開展建立了信心。為使學生掌握解題規律，避免學生盲目的題海戰術，減輕學生的課業負擔，變式的訓練是必不可少的。以往的變式題目，教師在黑板上，畫不完的圖，寫不完的字。如今，借助畫板可以完全改變這一狀況。

二、代數方面

1、正比例函數的圖像是過原點的一條直線，當k>0圖像過一、三象限，當k<0圖像過二、四象限，可以利用超級畫板新建一個參數k，當改變k的值時，圖像在動態的變化，變成負數時，圖像過二四象限。另外對于正比例函數的增減性可以很形象具體的展示給學生。我們可以再圖像上任找一點，然后度量出這點的坐標，當點從左向右移動的過程中，學生可以很形象的看到橫縱坐標的變化。所以我認為這比我們用黑板、粉筆、口述更能讓學生明白、掌握。

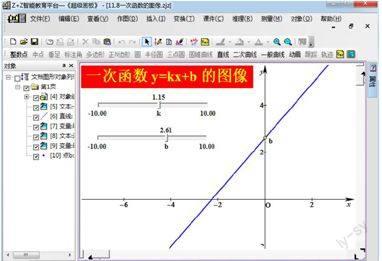
2、對于y=kx+b形式的一次函數來說，它的性質比正比例函數要多，要復雜，學生理解起來更困難。我們有幾何化板就可以化難為易，化繁為簡。更好的理解和記憶。在教學時我是這樣處理的。同樣是新建兩個參數k、b，當k值不變，改變b的值時，我們可以看到圖像在上下平移，再量一下圖像與y軸的交點坐標可以發現交點的縱坐標正好是b的值，所以學生可以得出結論：b的值決定了圖像與y軸交點的縱坐標;當改變k的值，b值不變時，可以發現，圖像的增減性發生了改變。所以可以說k的值決定了一次函數的增減性。當然還有其他的一些性質也能通過圖形看出來。這也是超級畫板軟件數形結合的魅力所在。

3、超級畫板在反比例函數中的應用與以上兩個類似，這里只介紹一個k的幾何意義的問題：在反比例函數圖像上任取一點P，分別向x、y軸作垂線，圍成四邊形的面積是|K|

當拖動點P時四邊形的面積始終保持不變，當改變K的值時四邊形的面積也在發生變化，但始終等于|K|。這個知識點，如果我們老師只是一味的去講，非常枯燥乏味學生不愿意聽，效果不會很理想，用這個軟件形象生動學生興致很高學的當然很好。另外在講反比例函數的對稱性時，我設計了一個動畫，學生看了之后很容易就理解了反比例函數關于原點的中心對稱性。還有如與的對稱性也可以通過動畫演示，學生很容易理解。

當我們使用《超級畫板》動態地、探索式地表現直線與圓的位置關系，圓與圓的位置關系，還有象圓錐的側面展開圖等等，都能把形象變直觀，實現空間想象能力的培養。實踐證明使用《超級畫板》探索學習數學不僅不會成為學生的負擔，相反使抽象變形象，微觀變宏觀，給學生的學習生活帶來極大的樂趣，學生完全可以在輕松愉快的氛圍中獲得知識。

甘肅省教育科學“十二五”規劃課題“超級畫板支持下的初中數學課堂教學有效性的案例研究”（GS[2013]GHB0466）階段性成果

【參考文獻】

[1]全日制義務教育數學課程標準 北京師范大學出版社，20017