基于認知負荷理論的數學“翻轉課堂”教學模式探究

楊麗恒 原文志 馬建宏

摘要：從認知負荷理論的內在認知負荷、外在認知負荷及關聯認知負荷視角出發，以初中七年級數學課程中的二元一次方程的翻轉課堂內容為課例，分析與探討翻轉課堂從教學模式上顛倒學習內容傳遞和內化順序的特征及從本質上降低認知負荷的心理學實質，以期為國內翻轉課堂的應用研究提供認知負荷內在機制的參考。

關鍵詞：認知負荷理論 數學翻轉課堂 教學模式

一、認知負荷理論

認知（cognition）是個體獲得知識和解決問題的操作和能力，即信息加工的過程和能力，而認知負荷是指進行信息加工時，認知資源被占用的比例。認知資源（cognition capacity）有限理論認為對學習內容的識別需要占用認知資源，當學習內容越復雜時，占用的認知資源就越多，而我們的認知資源是有限的，當認知資源完全被占用時，其他學習內容將得不到注意而不被加工，即認知負荷超載。1981年John Sweller將認知負荷的概念引入到教學領域，并提出認知負荷理論（Cognitive Load Theory，CLT），該理論基于資源有限理論和圖式理論，探討信息加工過程中工作記憶和長時記憶的關系以及對復雜學習和問題解決的影響，同時也成為多媒體教學設計的理論基礎，并為其提供理論框架[1]。

1.認知負荷理論的理論基礎

認知負荷理論結合人類認知結構特點，以認知資源有限理論和圖式理論為理論基礎，提出學習的過程就是圖式的獲得與圖式自動化的過程。

認知資源有限理論認為，工作記憶和長時記憶共同構成人類認知結構，其中工作記憶容量有限，在4～60秒的時間內只能對7±2個單位的信息進行加工，通過復述可以讓信息保持在工作記憶階段或進入長時記憶，如果要讓短時記憶的信息能夠進入長時記憶且更長久地保持在長時記憶中，需要使工作記憶的信息與長時記憶中的認知結構（圖式）產生意義上的聯系，使已有的認知結構起到穩固新知識點的作用。存儲于長時記憶的知識結構以圖式或系統化的方式存在，當需要使用時，可從長時記憶中提取到短時記憶階段并進行信息加工[2][3]。

圖式理論認為圖式是一種有組織的知識結構，它反映某類知識的基本特征和規律，憑這一類知識可以對一事物進行分析和歸類。使用圖式可以簡化人對事物的識別與分類，從而降低工作記憶的認知負荷。在數學學習過程中，學生通過大量的練習，可將圖式按照性質進行歸類、重新組織，建構出新的圖式，當遇到新的問題時，只需要根據問題特征，從長時記憶中“尋找——匹配”相關圖式，即可將新的問題置于已有圖式中進行歸類——選擇解決策略——解決問題，問題解決次數越多，圖式結構越精致化，最終在信息提取時達到自動化，從而節省認知資源空間，減輕工作記憶的認知負荷。

2.認知負荷理論的分類

Sweller從教學設計的角度將認知負荷分為三類，即內在認知負荷、外在認知負荷和相關認知負荷[4]。

內在認知負荷與學習內容的特征及學習者已有的知識經驗有關，學習內容的構成元素越少，則元素間的交互作用越小，內在認知負荷就越低；從學習者的內在知識結構來看，學習者長時記憶中存儲的與當前學習內容相聯系的知識經驗或圖式越豐富、越系統、越穩固，則內在認知負荷就越低。根據認知資源有限理論，工作記憶的容量是7±2個單位，即5～9個單位，看似很難突破，但是如果把每個單位看成是一個組塊（chunk），想辦法去增加每個組塊的容量，在有限的認知資源空間中，工作記憶的容量會數倍增大。例如，在數學學習中，一個數字可以作為一個組塊，一個公式也可以作為一個組塊，還可以將若干個公式根據其邏輯關系形成一個組塊。當然，學習者對每一個組塊單位要非常熟悉且信息提取達到高度自動化，而組塊內部的熟練化和自動化是在平時學習過程中逐步積累、訓練、鞏固而成的，因此，在問題解決過程中不需要占用更多認知資源空間，當要處理相關信息時，從長時記憶中提取到工作記憶，進行信息加工，從而降低認知負荷。

外在認知負荷與學習材料的呈現形式有關。呈現形式越合理，越符合學習者的認知水平，學習者信息加工的干擾因素越少，外在認知負荷就越低，越有利于學習。臺灣學者陳明璋在AMA認知與數字化教學的報告中提出，在呈現一段文字或一道題目時，最好將整段文字拆成若干個簡短的小句子，且每個小句子分開來寫，并將每個句子中的關鍵詞用不同的字體、字號或顏色呈現，這樣，學生在閱讀題目過程中會感覺不費勁，對重點能引起注意，且易于理解[5]。究其實質，就在于外在認知負荷的降低，因此在數學教學中，對學習內容重新組織，選擇恰當的呈現方式，從教學策略、多媒體使用手段等方面重新進行設計，從而降低外在認知負荷，尤其對于難度較大且邏輯性很強的問題，題目本身特征決定內在認知負荷較高，從內容的設計、多媒體呈現手段和活動策略等方面降低外在負荷就顯得尤為重要。

關聯認知負荷是學習者在工作記憶信息加工過程中的心理努力程度，心理努力越強，關聯認知負荷越高，相伴隨著情緒喚醒水平也提高，有利于促進學習者積極學習，心理努力在學習者學習時才能得以測量[6]。關聯認知負荷是促進學習者學習的有效認知負荷。

3.基于認知負荷類型的教學策略

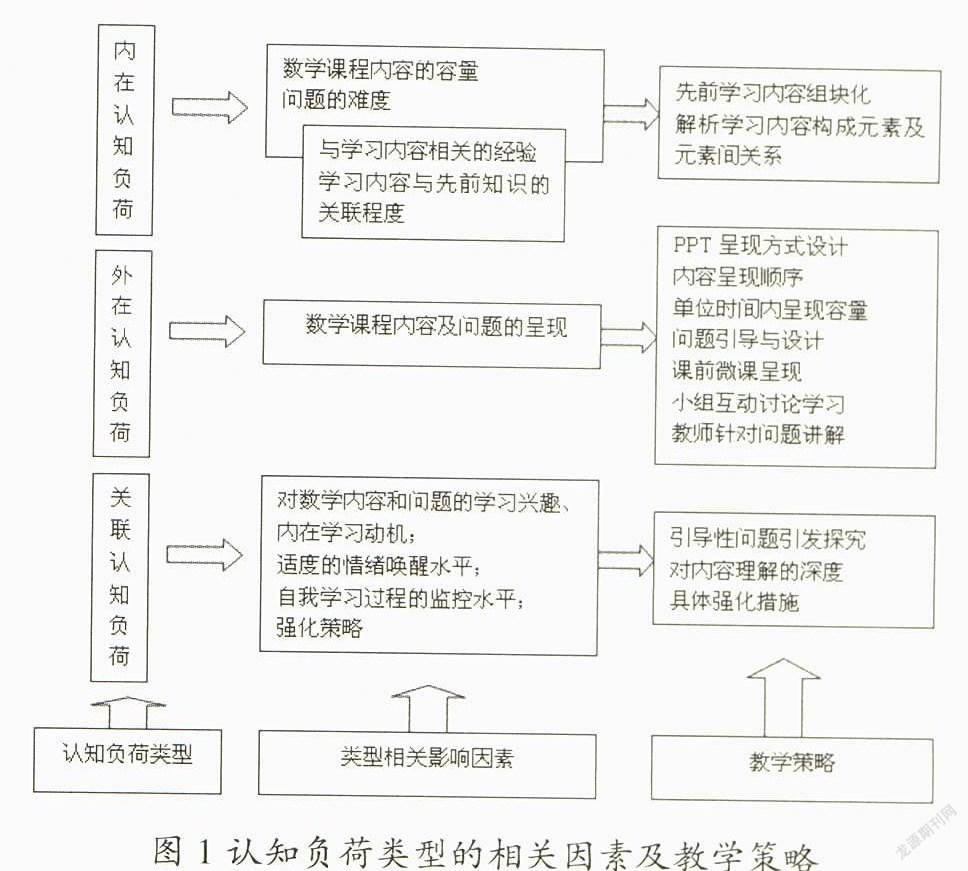
根據認知負荷理論的分類，剖析數學學習內容中與認知負荷具體類型相關的影響因素，并提出相應的教學策略（見圖1）。

二、基于認知負荷理論的數學“翻轉課堂”教學

1.翻轉課堂的發展

“翻轉課堂”（Flipped Classroom），其理念最早出現在19世紀，General Sylvanas Thayer在教學中總結了一套教學方法，即在課前學生通過教師提前發放的資料進行學習，課上時間用來批判性思考和小組協作解決問題，是翻轉課堂的雛形。Salam Khan將輔導資料制作成視頻，放到YouTube網站上，幫助學生解決了不能到課堂上課的問題，受到學生的喜愛，也收到世界各地的積極反饋，之后創建Khan研究所，對翻轉課堂起到關鍵性的推動作用[7][8]。美國“林地公園”高中化學教師Joe Bergmann & Aroe Sams用錄屏軟件錄制PPT演示文稿的播放與講解，給曠課學生看，很受學生歡迎，之后他們顛倒傳統教學模式，讓學生提前觀看錄制視頻，課堂時間用來解決問題并完成作業。這一模式推廣后，教學效果超乎預期[9]。

“翻轉課堂”的實質是翻轉了傳統的教師講授、學生接受的模式，學生在課前學習教師提前錄制的視頻和發放的學習材料，課堂時間用于小組討論、合作學習和問題解決，學生可根據自己的認知負荷狀況調整信息呈現時間和學習進度，從而減輕認知負荷，促進工作記憶的信息加工效率。從心理學的角度看，翻轉課堂教學模式從本質上是降低了認知負荷，使學習者的認知資源得到更合理的分配，從而獲得更好的學習效果。

2.基于認知負荷理論的數學“翻轉課堂”課例分析

以銀川市某初級中學“翻轉課堂”教學為例，選擇七年級數學課程中的《二元一次方程》課例進行分析，在學生原有認知結構中已有一元一次方程的相關圖式，在學習本節內容時需要將相關知識從長時記憶中提取出來進行匹配與區別，以加深對新內容的理解。

基于對二元一次方程與一元一次方程概念的區別、二元一次方程解的概念及解的不唯一性、以及如何用一個未知數的代數式來表示另一個未知數等內容的闡釋，教師制作了一個時長7分鐘的課前微課，讓學生在課前進行學習。

從認知負荷理論的角度分析，關于一元一次方程的內容，學生已經學習過，且假設經過之前大量的練習已非常熟練，從長時記憶提取到工作記憶的過程已達到自動化，可將這部分內容作為一個組塊（chunk）單元。由于高度自動化，在工作記憶中進行信息加工時，其所占用的認知資源空間非常有限，因此，對這部分內容的信息處理所需的認知負荷較低，可以節省更多的認知資源去加工和處理二元一次方程相關的內容。

微課時長7分鐘，學生在學習過程中可以完整的聽完，而對于不太理解的部分倒回來重新學習，需要記筆記時就暫停。這個環節看似非常簡單，卻非常有利于降低內在認知負荷。在傳統課堂中，很多學生普遍的感受是教師在講到某個環節時，由于思路沒跟上或注意力稍不集中，某個承上啟下的關鍵知識點就錯過了，以至于后面的內容也不太理解，而微課的可重復性，使學生在單位時間內要處理的信息量下降了，內在認知負荷也降低了。

教師在導學案中根據問題的難易程度，有梯度、漸進式地提出問題，讓學生根據自己的學習進度和理解程度來進行回答。如讓學生嘗試著給二元一次方程下定義——提煉二元一次方程的特點——試圖自己列出二元一次方程的式子——通過實例為二元一次方程求解等具體問題。學習材料的呈現順序與外在認知負荷有關，由易到難的認知過程有利于認知負荷的降低，其原理在于教師最初給學生呈現的學習內容是最初級的，最易于解答的，因此它的內在認知負荷較低；在學生掌握之后，進入到稍有難度的內容中，而之前學習過的較簡單的問題已不再或較少占用認知資源空間，留下更多空間學習稍難的內容。以此類推，按照難易程度及邏輯順序來安排學習內容，總能夠為內在認知負荷較高的更難的內容留下更多的認知資源空間，從而達到降低其外在認知負荷的目的。

在學生課前學習過程中，會產生一些疑問，然后在課堂上進行小組討論，教師在學生討論的基礎上，除了要對學生存在的基本問題進行解答之外，還要進一步提出一些引發學生深度思考的問題。如利用學生在例題中對二元一次方程求解的過程，引導學生類比一元一次方程的解的概念去歸納出二元一次方程的解的概念；針對二元一次方程解的不唯一性，讓學生對某個二元一次方程的實例算出不同的解，并針對學生的學習給予及時的反饋，從而加深對內容的理解；針對二元一次方程求解的方法，引導學生體會用關于一個未知數的代數式去表示另一個未知數的過程，其實質是解y的一元一次方程，從而將數學主元思想滲透融合到學生的認知結構中。教師讓學生進行小組討論，并提出引發學生思考的有一定深度的問題，可以激發學生學習熱情及內在動機，使學生進行探究性學習，并在一定程度上保持情緒喚醒水平，同時，教師根據學生對題目的解答給予及時反饋，實質上是一種強化策略，這些均會適度增加關聯認知負荷。

總之，從認知負荷理論的角度思考，會發現翻轉課堂教學模式對學生的學習過程進行了重構，“信息傳遞”在課前以微課的形式進行，其可重復性決定單位時間內需要接受和吸收的信息量下降，從而降低內在和外在認知負荷。“吸收內化”是在課堂上通過互動來完成的，學生間的相互交流有助于促進學生知識的吸收內化；教師提前了解學生的學習困難，從而在課堂上給予有效的輔導并提出引發學生深入思考的問題，提高了關聯認知負荷。

參考文獻

[1] 宋艷玲，孟昭鵬，閆亞娟.從認知負荷視角探究翻轉課堂——兼及翻轉課堂的典型模式分析[J].遠程教育雜志，2014（1）.

[2] 彭聃齡.普通心理學[M].北京：北京師范大學出版社，2011.

[3] 陳燕，羅增儒，趙建斌.從認知負荷理論看數學錯誤[J].數學教育學報，2009（4）.

[4] 龐維國.認知負荷理論及其教學涵義[J].當代教育科學，2011（12）.

[5] 陳明璋.AMA認知與數字化教學[R].國培計劃——培訓團隊研究項目天津師范大學數學班，2014.

[6] 陳巧芬.認知負荷理論及其發展[J].現代教育技術，2007（9）.

[7] 張渝江.翻轉課堂變革[J].中國信息技術教育，2012（10）.

[8] 焦建利，賈義敏.國際開放教育資源典型案例——一個研究計劃[J].現代教育技術，2011（21）.

[9] 張金磊，王穎，張金輝.翻轉課堂教學模式研究[J].遠程教育雜志，2012（4）.

[作者：楊麗恒（1976-），女，寧夏青銅峽人，寧夏大學教育學院心理系講師，碩士；原文志（1962-），男，山西絳縣人，太原師范學院數學系教授；馬建宏（1973-），男，寧夏中衛人，寧夏大學教育學院副教授，碩士。]

【責任編輯 郭振玲】