挖掘課本例習題的教學價值,提高數學教學實效
沈良琴
摘 要: 例題習題教學是數學課的主要環節,它的有效性決定著教學目標落實的程度.認真剖析課本例題、習題,對典型的例題、習題從多角度挖掘其典型的應有的教學價值,這樣不僅能加深學生對數學概念、法則、定理等基礎知識的理解和掌握,還能讓學生在解題的準確性、靈活性和敏捷性上得到有效的提高.
關鍵詞: 課本習題 多角度挖掘 變式拓展 教學實效
教材上的例題有最規范的解答過程,具有示范性、典型性和探究性,是課本的精髓,它和習題一起控制了教材的深度和知識輻射范圍.教師應充分認識課本例習題所蘊涵的價值,注重對課本例題和習題進行充分的挖掘和研究,對其深化和發展、全方位探索,挖掘其內含及外延,把新舊知識有機組合起來,達到優化認知、開闊眼界、活躍思維、提高能力的目的.
我以蘇科版教材中的例習題為例,就數學課堂教學中如何結合教材特點,發掘課本例習題的教學價值,開拓學生思維,提高數學教學實效談談體會.
一、構建一節課中完整的例題體系
要想使例題教學的效益最大化,在課前就必須對一節課的“例題”構建一個體系,對例題的數量、類型、前后聯系進行整體設計.
例如:我在設計九下教材7.6《解直角三角形》第二課時時,結合課本例題進行了如下設計,例題體現構造直角三角形,選擇合適的三角函數求線段的長.
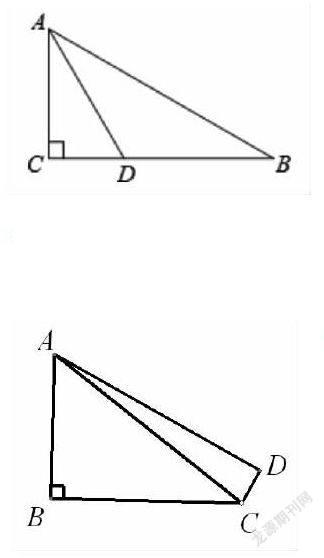
例1.如圖所示,△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分線,若BD=10,求AC長.
例3.如圖所示,在四邊形ABCD中,∠B=∠D=90°,∠BAD=60°,若CD=2,BC=11,求AC長.
這三道例題層層遞進,例1利用“等角對等邊”求得AD=10之后,直接利用三角函數可求得AC的長.例2與例1圖形相同,所求相同,只是將已知條件做了變化,在Rt△ACD中利用三角函數得到線段之間的比例,根據比設未知數,再在Rt△ABC中利用勾股定理列方程求解.例3需添加輔助線進行解題,延長BC、AD交于點E,三角函數和勾股定理結合便可解決該問題.
二、變式拓展,挖掘例習題的廣度和深度
教材中的例題是最好的例題資源,但如何用好這些例題,如何在此基礎上進行生發,我嘗試以下方法進行例題教學——一題多問,一題多變,多題一解,錯題辨析等.
例如:在九下二次函數的應用教學時,我進行了如下設計.
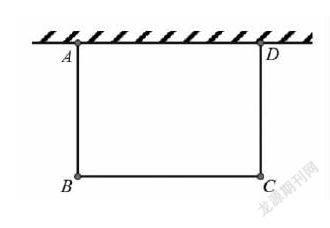
(1)寫出S與x之間的函數關系式;
(2)當x取何值時,面積S最大,最大值是多少?
補充提問:若此問題中將“墻的長度足夠長”改為“墻的最大可利用長度為15m”,解題的結果會發生改變嗎?
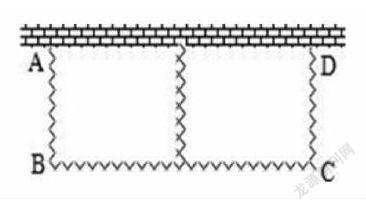
(1)請求出S與x的函數關系式及自變量的取值范圍.
若能,請求出最大面積;若不能,請說明理由.
這兩個例題的問題背景、解決方法有類似之處,題設條件部分發生了改變,所求結論表達形式稍加改編,因此一題多變、多題一講是很必要的.它可以使學生感覺到知識點的核心之處,只要將它的內涵與外延挖掘徹底,進而靈活運用就可以了.
三、好的例題一定要有匹配度高的練習支撐
例題教學就如扶著孩子學走路,最終孩子要學會自己走路,這一過程必須在相對熟悉的題型中自主嘗試,所以好的例題一定要有匹配度高的練習支撐.
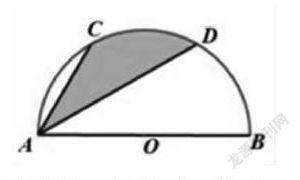
為了分解難點我將該題設置了4個小問題:(1)求弦CD的長.(2)弦CD與AB有什么關系,請說明理由.(3)陰影部分面積與半圓的面積有什么關系,請說明理由.(4)若點A是AB上一動點,求陰影部分面積.
該題將要求的陰影部分面積轉化為扇形COD的面積,為了計算不規則圖形的面積,常常需要變動圖形的位置或對圖形進行適當的分割、拼補、旋轉等手段使之轉化為規則圖形的和、差關系.我設計了兩個習題作為配套練習:
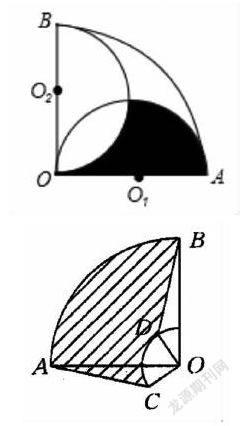
2.圓心角都是90°的扇形OAB與扇形OCD如下圖所示那樣疊放在一起,連接AC,BD.
(1)試說明△AOC≌△BOD.
(2)若OA=3cm,OC=1cm,求陰影部分的面積.
課本中的每一個例題、習題的設置都有其目的和作用,教學中只有認真鉆研教材,領會教材編寫意圖,深刻理解課本例習題的重要價值,根據教學的要求和學生的實際,將這些例習題進行進一步探究,引導學生全方位、多角度地思考,才能提高數學教學實效.
參考文獻:
[1]數學課程標準解讀(全日制義務教育)[M].湖北教育出版社,2011.
[2]邵瀟野.例談課本幾何習題的拓展研究[J].中國數學教育,2007(10).
[3]張曉靜,邵光華.美國數學教材例習題設計分析與啟示.中學數學教學參考,2012(5)(中旬).

