中學生數學解題思維能力提升策略研究

文/鄧奎

中學生數學解題思維能力提升策略研究

文/鄧奎

摘要：問題是數學的心臟，解決問題的需要推動著數學的發展，我國《普通高中數學課程標準》把“數學地提出、分析和解決問題(包括簡單的實際問題)的能力”作為數學課程的主要目標。對于中學生而言，由于學生缺乏科學的指導，學生在面對一些難題的時候往往一籌莫展，一些學生在面對一些中等題的時候都顯得很棘手。筆者通過對以下幾個方面的闡述試圖探討提高學生的數學解題能力的有效策略。

關鍵詞：問題;解題;數學思想

中圖分類號:G613.6

文獻標志碼：碼：A

文章編號：號：2095-9214(2015)11-0070-02

1.大膽聯想——提升思維的廣度

很多數學問題都是通過一些我們所熟悉的問題，經過再加工而改編來的。我們在解題過程中，應注意數學的聯想思維，將不熟悉轉化為我們所熟悉的，將復雜的轉化為簡單的。要對題干出現的式子進行合理的改造，將式子轉化為我們熟悉的形式。在解題過程中，要充分利用數形結合思想。

(1)適當添加或刪減題干中的信息，將結構轉化為我們熟悉的

對于一個數學題目，有的時候我們總感覺這個問題很有相似的地方，這個時候，我們就要適當的添加或刪減題干中的某些信息，將問題轉化為我們平時所熟悉的，再聯想熟悉的題目的解決方法，從而達到解決問題。

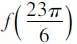
解析：對于f(x+π)=f(x)+sinx，給我們的感覺是很熟悉，但是與我們以前見過的又有些不一樣。但是如果我們將題干中的sinx 去掉，就得到這樣一個式子f(x+π)=f(x)。顯然這表示函數f(x)的周期性，然后我們想到求函數周期性我們要采取的方法是迭代法，從而得到下面的式子：f(x+2π)=

f(x+π)+sin(x+π)，進一步化簡可以得到：f(x+2π)=f(x+π)-sinx，聯立題干的信息，得到：f(x+2π)=f(x)，所以得到函數f(x)周期為2π。

(2)巧妙構造函數，利用函數性質解決問題

當題干中出現幾個形式相似的式子，我們將未知數相同的式子結合在一起，通過對式子的整理，然后結合幾個結構完全一致的式子，進而聯想到構造一個函數來解決問題。

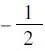
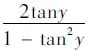
這種類型的問題經常出現，這就需要我們對式子進行仔細觀察，然后聯想構造函數，利用函數的性質解決問題。

2.深刻理解——提升思維的深度

很多學生在解題過程中遇到困難很多時候不是因為對知識的不清楚，而是對數學思想方法的缺失。高中學常見的數學思想有：數形結合思想、分類討論思想、函數與方程思想、猜想歸納思想等等。

(1)數形結合思想

數與形是數學中的兩個最古老，也是最基本的研究對象，它們在一定條件下可以相互轉化。中學數學研究的對象可分為數和形兩大部分，數與形是有聯系的，這個聯系稱之為數形結合，或形數結合。它可以幫助人們將抽象的問題變為直觀、形象，便于思考和研究。

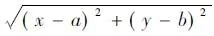
A.(-∞,-6)∪(6,+∞)B.(-∞,-4)∪(4,+∞)

C.(-∞,-2)∪(2,+∞)D.(-∞,-1)∪(1,+∞)

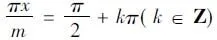
當我們遇到一些常見的具有幾何意義量的時候，我么要馬上聯想到數形結合，將代數問題幾何化。

(2)分類討論思想

當我們遇到一件事情不能按統一標準統一處理時，常常先分成幾種不同的情況或分類，再制定不同情況或種類的處理規則或辦法，然后分別加以解決，這中間蘊含的就是分類處理(討論)思想，基于此思想所形成的數學方法就是分類討論方法(通常也稱為分類討論思想方法)。

當我們在處理問題的時候，遇到一個步驟有幾種可能的時候，我們不知道書寫哪種的時候，此時我們就要進行分論討論。

解析：Sn=a1+a2+a3+...+an-1+an=2+22+2×3+...+an-1+an，我們在書寫過程中，對于an我們不知道該書寫什么，因為我們不清楚最后一項為奇數還是偶數。此時我們就要進行分類討論。

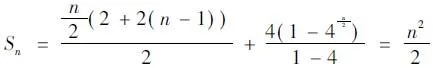
其他數學思想方法此處不再一一詳細介紹。

3.一題多解——提升思維的靈活度

一道題往往不止一種方法，學生在解題過程中要不斷探索積極思考，考慮一個題是否有其他的解法。而對于一個類型的題目，學生要學會總結與歸納，這些一類的題解決方法是一定的，真正做到舉一反三。

例：已知a,b∈R+ab=a+b+3，求ab的最小值

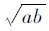
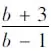
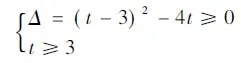
事實上，對于多元最值問題，我們總是從這幾方面去思考的，所以這幾種方法也可作為多元最值問題的解題通法。學生在學習過程中要經常進行總結，對于一個精妙的解法要進行深度挖掘，嘗試下它是否對一類題都成立，形成多題一解。

4.結語

我們學習數學不僅僅是為了解決數學問題，解決數學問題有利于提升我們的思維能力，能夠鞏固我們平時學習到的數學知識，加深對知識的理解以及對數學思想的掌握。當我們遇到數學難題的時候，首先要仔細閱讀題干，從題干中的一些提示聯想到我們平時所學習的知識，一定要進行合理的轉化，將不熟悉的轉化成熟悉的，將復雜的轉化成簡單的，將代數式轉化成幾何意義的量等等。平時要對一些常見的數學問題進行總結，體會相應的問題蘊含了哪些知識點，以及包含了哪些數學思想等等。同學們在平時的數學解題中可以參考下筆者的這些想法，希望能夠提高中學生的數學解題思維。

(作者單位：西華師范大學數學與信息學院)

參考文獻：

[1]王林全，吳有昌.《中學數學解題研究》[M].北京：科學出版社，2009.

[2]張世林，向宏濤.《一道不等式填空題的教學實錄》[J].《數學通訊》，2013，(9).

[3]王平定，朱賢良.《高效解題的兩個角度：“一題多解”與“多題一解”》[J].《數學教學研究》，2014，(8).

[4]G．波利亞.《怎樣解題》[M].上海:上?？萍冀逃霭嫔?，2007.