凸函數在初等不等式中的應用

凸函數在初等不等式中的應用

文/磨雪梅

摘要：凸性是函數的一個重要性質。對函數凸性的研究, 特別是在不等式的推導方面很有用處。近年來在高考命題的邊緣也涉及了凸函數的一些初步理論。

關鍵詞：凸函數;應用;不等式

中圖分類號:G613.6文獻標志碼：A

1. 引言

凸函數是一類重要的函數，它在許多相關學科里都有著重要的應用。對函數凸性的研究,特別是在函數圖形的描繪和不等式的推導方面,凸函數起著十分重要的作用，在高考命題的邊緣也涉及了凸函數的一些初步理論。本文主要介紹了凸函數的定義,接著根據定義引出了著名的琴生不等式,運用凸函數在初等不等式的證明方面列舉了一些例子如一般的算術不等式、指數不等式、對數不等式等來說明在其中的應用，包括列舉了個別高考題利用凸函數來解是相當簡便的。

2. (1) 凸函數的定義

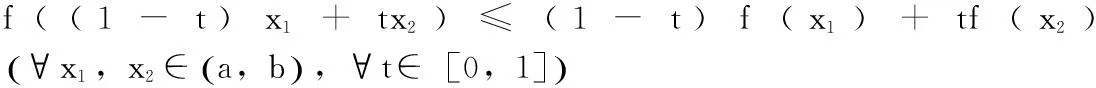
(2) 關于凸函數的一個重要不等式——Jensen 不等式

凸函數的推廣(Jensen 不等式) (J·L·W·V·Jensen丹麥數學家，1859～1925年)，利用它可以解決許多最值問題且比較方便。下面給出它的內容。

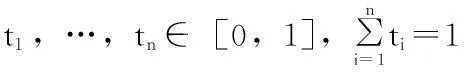
Jensen 不等式是凸函數的一個重要性質,因為每個凸函數都有一個Jensen 不等式,因而它在一些不等式證明中有著廣泛的應用，下面我們會舉例來說明這一點。

3. 凸函數在初等不等式證明中的應用

例1(94全國文科高考題)

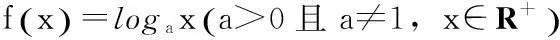
凸函數的概念及性質定理是中學數學的邊緣知識，因此，探討和總結凸函數的性質及應用，對于深刻理解和牢固掌握函數的概念和性質，培養學生抽象思維和創新意識具有重要作用。

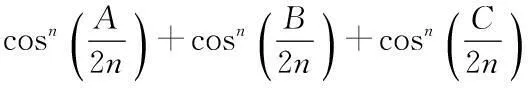
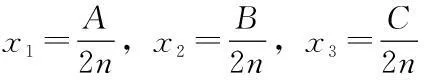
類似的不等式還有:A,B,C是三角形的三個內角,則有:

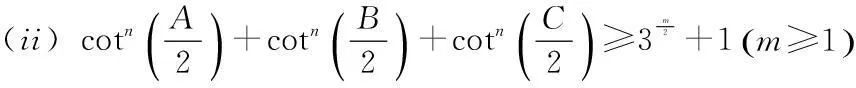
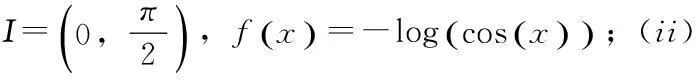
用凸函數來解決不等式問題時,關鍵是找到相關的凸函數,大多數情況下是容易找的,但是有的情況需要進行變換或變形,如例2。

4.結束語

可以看出,凸函數在推導初等不等式方面是十分有用的，本文簡潔、清晰地揭示了凸函數的內涵與外延。介紹了應用廣泛的琴生不等式和應用，文章結尾通過利用凸函數來解決一些實際問題,即證明了若干初等不等式,使解題方便快捷。借此說明了凸函數在不等式證明中的作用和研究凸函數的重要性,使本文的探討具有一定的意義。

(作者單位：廣西南寧市新陽西路學校)

參考文獻：

[1]浦義書,陳露.凸函數概述.高等數學研究.西北工業大學出版社.2006.7.P34-P36

[2]王新力.琴生(Jense)不等式的應用.杭州教育學院學報,Vo1.19,No.3,May.2002.P10-P13

[3]孟杰.凸函數的基本概念[J].數學通訊.1983.4.P2-P4

[4]陳秋華.也談利用凸函數證明初等不等式.高等數學研究.西北工業大學出版社.2006.9.P40-P42 .