數形結合在初中幾何教學中的應用

何鐵佳

摘 要： 在初中數學教學中，數字和圖形是有利于教師教學和學生學習的重要因素，把二者結合起來，就是數形結合，利用這種思想來解各種幾何問題，比如平面幾何的大題。本文主要闡述運用數形結合在初中教學中的作用和應用，把數形二者結合運用到教學中，使之發揮重要作用，達到教學目的。

關鍵詞： 數形結合 圖形和數字的轉化 幾何教學

一、引言

在初中數學教學中，我們應不斷地創新，用直接更有效的方法教學，不應一味死板地講授，教師應該數字和圖形之間建立聯系，很多數字題都可以用圖形加以詮釋，這樣可以很直觀地讓學生明白解題思路，把抽象的數字問題轉化成簡單的圖像，能讓問題變得更具體，讓學生理解得更透徹，領悟得也會更快。近幾年的中考中，數形結合類型的問題不斷出現，所以教師應加強這方面的練習，讓學生融會貫通，加以熟練運用。“數形結合”就是將數字在圖形上表現出來，從而運用圖形將數解出來，實現二者之間的轉化。接下來討論課堂上的“數形結合”。

二、數形結合的應用

數學中很多問題都很抽象，學生只能夠想象，然而，這是很困難的，教師在課堂上如果能夠用圖形直觀地表達講解，效果就會非常顯著，將抽象的問題轉化成具體的數學知識，幫助學生有效地加以理解運用，從而提高教學水平。在初中數學中，對于利用二維的平面直角坐標系解答一次函數的問題是很有幫助的，使問題變得簡單直接。幾何大題中，可以運用圖形解不等式，在圖形中找到解決問題的辦法，比如作一條輔助線，把抽象的圖形描繪出來，有助于快速解出問題。這種方法也可以叫“圖解法”。

一般來說，代數問題不運用圖形也是可以解決的，但用幾何中的圖形表達會更具體直觀，把二者結合，有效轉換會更有效果，從而解決問題。在圖形的幫助下可以優化解題，接下來舉兩個例子加以討論，以華東師大版數學教材為例。

（一）數形結合在三角形中的應用

在三角形這一部分課程的學習中，最主要的是抓住圖形之間的關系，通過數與形的結合，更具體地分析各個之間的關系。

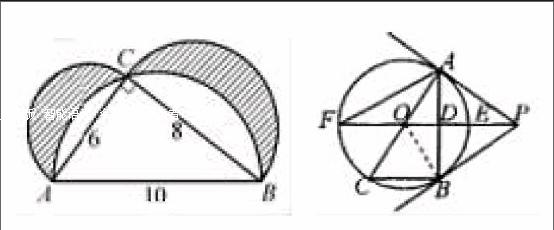
案例1：（八年級上冊，練習14.1）如圖，已知直角三角形ABC的三邊分別為6、8、10，分別以它的三邊為直徑向上作三個半圓，求圖中陰影部分的面積。

這道題通過圖形可以很清楚地看到其解法，圓、三角形的半徑邊長都已給出，先求出以10為直徑的半圓的面積，用大面積減去三角形的面積即得出兩個圓弧的總面積；再算出兩個小半圓的面積之和，用和減去兩個圓弧面積和。即為我們所要求的陰影部分的面積。

本題通過“數形結合”的方法，使學生可以清楚自己的解題思路，幫助學生更好地理解，提高學習興趣，在作圖過程中，復習和鞏固知識，培養學生的思維能力和動手能力。通過這種數形結合的方法，學生會更加愛數學，增強了求知欲望和學習動力，將數轉化到圖形上，會更直觀易懂。

（二）數形結合在圓中的應用

在與圓有關的位置關系中，各種與圓不同的位置關系中都可以用數形結合的思想解決問題。

案例2：如圖，PB為圓O的切線，B為切點，直線PO交圓O于點E，F，過點B作PO的垂直線BA，垂足為點D，交圓O于點A，延長AO與圓O交于點C，連接BC，AF，

（1）求證：直線PA為圓O的切線；

（2）試探究線段EF，OD，OP之間的等量關系，并加以證明.

分析：

（1）由圖形可以看出三角形AOP與三角形BOP是全等三角形，而題中又給出PB為切線，則可以證明出PA也為圓O的切線。根據圖可以很清楚地知道一些東西，看出圖中的思路，也就有了解決這道題的思路，有圖就可以很清楚地解答。

（2）在這道題中也可以先根據圖形進行猜測，再證明自己的猜測就會很容易。

在解答這類題時，如果能夠靈活運用數形結合思想，就會使問題變得簡單化，如果只是一味地用數字或單獨的圖形解決問題，就會遇到很大的麻煩。采用數形結合，可以生動而形象清楚地看到我們的需求，解決我們的問題。

（三）數形結合在函數關系中的應用

在初中，我們所接觸到的函數大部分為正比例函數、反比例函數、一次函數和二次函數，在解決函數問題中，數形結合思想通常也是運用最方便的一種解決辦法。函數問題不單單是一些代數之間的問題、聯系，它通常伴隨著一些函數圖形的應用，也是通過這些圖形提出更多的問題。在函數關系中，更應該注重函數圖像各個分段的特征，結合這些特征與所問的問題相聯系，從圖像中找到突破點，再結合數據分析，數形結合輕松解決問題。

三、數形結合思想應用的意義

數形結合，字面意思就是數與形的結合，遇到難得問題時，通過數形結合的思想可以讓問題簡單化，也可以使枯燥的數學課堂變得更加有趣，激發學生的學習興趣，從而輕松地了解并掌握需要掌握的知識。通過數形結合，不僅僅將數與形結合在一起，同樣也是抽象與具體的結合，活躍課堂氣氛，使學生輕松掌握課堂知識，也培養了學生的抽象思維。

四、結語

在數學教育中，數形結合思想是數學思想中一個重要的組成部分，對數學問題的研究解決起了很大的幫助作用。“數”與“形”原本就是數學中重要的兩部分，數與形的結合，兩者之間的相輔相成，使數學問題變得簡單易懂，把原本枯燥的數字用形象、直觀、簡單的圖形表示出來，使學生的想象思維變得廣闊，也提高了學生的分析能力。數形結合思想在數學教育界產生了重要影響，已成為數學工作研究者一大解決思路，以后會更深入。

參考文獻

[1]初中數學教材（華東師大版）.

[2]數形結合思想之教學研究.南京師范大學，2004.

[3]巧用數形結合解題.2006.