小學數學結構化教學的實踐與思考

【摘要】通過整合知識板塊、幫助思維結構化、倡導教學結構化來探討小學數學結構化教學，并從實踐中明確樹立系統教學理念，將不同領域的知識及其育人價值通過整體架構、有機滲透，融合于教學過程中，有助于發展學生的數學核心素養。

【關鍵詞】結構化教學；整合；思維；核心素養

【中圖分類號】G623.5 【文獻標志碼】A 【文章編號】1005-6009（2016）06-0035-03

【作者簡介】徐微，江蘇省鎮江市中山路小學（江蘇鎮江，212000），一級教師，鎮江市京口區數學學科帶頭人，江蘇省小學數學課程教材改革實驗先進個人。

如今，在學校日常教學中依然存在著這樣兩個問題：一是教師缺乏對數學知識的整體結構認識，過分依賴教材的單元和課時劃分，局限于單課時教學，割裂了知識結構，削弱甚至偏離了數學學科的課程目標；二是教師缺乏對學生學習過程的整體設計，滿足于當前情境或活動的設計，策劃的視野短期化，忽略甚至局限了學生的數學思維和學習能力的長期培養。作為教師應該樹立系統教學理念，將不同領域的知識及其育人價值通過整體架構、有機滲透，融合于教學過程中，使學生的學科素養得到整體提升。基于此，筆者進行了如下的實踐與思考。

一、小學數學結構化教學的實踐策略

1.整合知識板塊。

結構的關聯能使知識的教學和能力的發展呈現一條清晰的脈絡，但這樣的結構設計不是唯一，不應成為教學的桎梏，同樣這樣的結構也不應該固化，使教學陷入枯燥的模式化。在教學中，教師可以依據單元知識之間的并聯關系、遞進關系靈活設計教學流程。

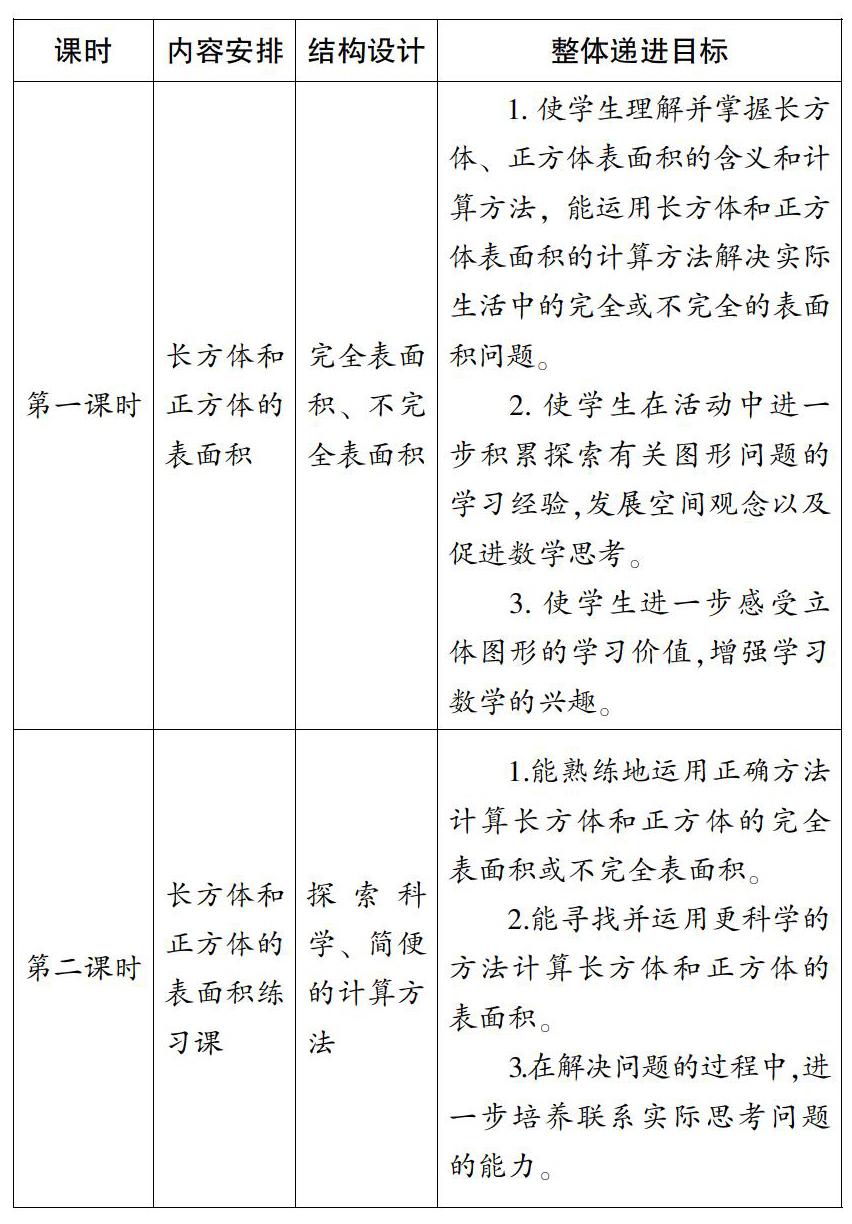
（1）整合課時知識。受40分鐘教學時間的限制，有些內容被劃分成兩個或三個獨立課時，比如：在蘇教版六上《長方體和正方體》單元的教學中，“長方體和正方體完全表面積計算”和“長方體和正方體不完全表面積計算”這兩個課時的學習都是建立在對這兩種立體圖形的認識和研究了它們的展開圖的基礎上進行的，兩課的內容聯系緊密，探究方法、教學過程基本一致。于是，筆者嘗試對這兩課進行如下調整：

通過實際教學，證明嘗試是成功的，學生不僅能很好地達成學習目標，還能對長方體和正方體表面積計算的探究過程形成清晰認識，對實際遇到的各類完全表面積或不完全表面積均能正確靈活的計算。這樣深入知識內部去整體把握、科學設計，擺脫了原有課時的桎梏，充分尊重學生的學習需求，靈活使用教材，從而達到讓教材為教學服務、為學生發展服務的目的。

（2）整合單元知識。在實際教學中，我們發現有些年段單元知識前后的聯系非常密切，不僅有利于教師在教學中保持知識的整體性，還有利于學生感受知識的整體性。例如蘇教版五上第三、四、五單元，先后進行《小數的意義和性質》《小數加法和減法》《小數乘法和除法》的教學，對小數的學習通過認識和運算去整體把握，塊面完整。而蘇教版教材中分數知識的塊面劃分就有了區別，三、五、六年級均涉及，其中六上第二、三單元學習《分數乘法》和《分數除法》后，第四單元研究《解決問題的策略》，然后第五單元再學習《分數四則混合運算》。從教師角度看，不利于教學的整體結構；從學生的角度看，不利于學生頭腦中對知識的整體建構。基于此，筆者在實際教學中將《分數乘法》《分數除法》《分數四則混合運算》三單元整體教學，脈絡清晰，一氣呵成。

2.幫助思維結構化。

結構化教學是一項長期的工程，其價值不僅限于知識的形成，更多地體現在學生對知識結構的把握和把握結構后自主建構學習的積極狀態。

（1）整體感悟。思維整體的結構化在復習課中體現最明顯，復習不是對單元知識的簡單重復，而是依據復習內容采用新的復習策略，以此幫助學生保持較高的復習興趣。如復習蘇教版六上《分數乘法》單元時，筆者要求學生課前自我復習，并根據自己的理解制作知識結構圖以展示整個單元的知識體系，課上分組交流匯報。通過這樣的形式，學生能夠整體地把握內容之間的關系，并能積極地進行討論，繼而在整體感悟的基礎上，主動建構和完善自己的認知結構和思維方式。

（2）學會遷移。在由教到學逐步放手的過程中，遷移知識形成的過程性結構尤為重要，教師帶領學生在一定程度上還原前人發現和發展某一領域知識的過程，并將這一過程結構化，幫助學生了解和掌握這個發現探索的過程性結構，然后自覺遷移到教材以外的探索中。如從探索加法、乘法運算律引導學生去驗證減法和除法中是否存在類似的運算律，從探索平行四邊形面積拓展到三角形的面積計算。教師只有學會利用遷移，才能激發起學生更多的運用和創造熱情。

（3）培養能力。基于結構的教學，要讓學生意識到結構的存在，并自覺地運用結構展開學習。因此，每一單元、每一學期或每一學段學習結束后，指導學生進行復習與整理，會讓學生體會到知識的系統化和條理化。從系統梳理到整體結構化地把握知識，從尋找知識間的差異到溝通知識間的內在聯系，從個性化整理到創造性呈現，學生對整個過程的經歷與體驗有利于學生形成綜合的學習能力，發展數學核心素養。

3.倡導教學結構化。

教師要在深入解讀課程標準、正確把握教材、明晰學生學習起點的基礎上，科學制定目標。在縱向上，依據學生年段特點，從學習心態、知識積累、能力、習慣等方面進行分析；在橫向上，緊扣知識間聯系，預設學生發展的可能，以及學生面對具體的數學知識時的心理狀態，分析學生現有知識經驗對新知學習的影響。同時，科學評估學生的潛能，積極創設有利于學生學習和探索的思維空間和心理空間。關注不同基礎學生在新知學習過程中的不同表達方式，關注差異性。例如：感悟統計思想方法貫穿整個小學階段，從把相同的放在一起數到畫勾、畫正字、單式統計表、復式統計表、條形統計圖、折線統計圖、扇形統計圖。再比如：學習比較的思想，從最初比較兩類事物的個數，到數形結合給出條件比較，成了實際問題的雛形；從直觀實物的比較，到抽象出線段圖，這一過程把數學思想方法的長期感悟、持久熏陶，特別是結構的整體性表現得淋漓盡致。

二、小學數學結構化教學的價值認識

從列維的結構主義到皮亞杰的認知結構理論、布魯納的“學科基本結構”思想，以及奧蘇伯爾提出“新知識的學習必須以已有的認知結構為基礎”這些觀點，無一不與“結構”相關。整體結構教學就是要通過回顧、提煉和反思逐步將知識結構內化為學生學習的方法結構，成為新的學習工具。它包括三個層面的結構：

一是展開結構，在前后關聯的知識之間有著相似的呈現方式。如在整數中按照“數的意義”、“數的運算”以及“運算的規律”展開，同樣方式在小數、分數教學中也遵循，這就是知識展開方式的相似性。同樣，在“認數”教學中，不同年級數概念教學都有著相同的展開邏輯：數的意義→數的組成→數位→讀寫→數的大小比較。隨著對數認識的逐步拓展，這些“知識結構”將會潛移默化地被學生個體“吸收”而內化為“認知結構”，幫助學生在整體上對數學知識和方法進行把握，改變碎片化處理數學知識和方法的現象，增強學生學習數學的整體意識，提高學習效率。

二是過程結構，同一類知識有著類似的教學過程。例如教學“運算律”時，一般都按“猜想→驗證→概括→拓展”進行；“量的計量”教學按照“材料感知→操作感悟→形成概念→運用鞏固”這一過程推進，這些就是相關知識教學的過程結構。認識到這種過程性結構的存在，教師就可以從起始內容開始，努力引導學生了解和把握，使得在后續的學習中，學生能主動遷移，開展學習研究活動。結構化地展開教學過程，學生獲得了獨立學習的有效路徑，便能投入積極主動的學習過程，成為知識、能力和方法的主動建構者和創造者。

三是方法結構，學生在獲取數學知識的過程中經常采用相同的學習方法。如：學習整數加減乘除的運算時，通常都采用“講算理→明算法→多應用”的方式；學習正方體、長方體、圓柱體的表面積計算時，通常采用“想特征→試操作（剪開成平面圖形）→說聯系→多應用”的方法。當學生明晰了這樣的結構，自主學習才有了可能，在遇到相似的問題時不再依賴教師，而是自己進行方法結構的正遷移。在這樣的結構教學中，教師關注學生的不僅僅是獲取知識量的多少、解題熟練程度和是否掌握了解題技巧，而是關注學生是否獲得了思維方式與行為方式的雙支撐。這種支撐能促進學生把已掌握的知識自覺地提煉成簡潔的原理性結構，從而使學生擁有探究新知識和新事物的能力，如此，將極大激發學生學習數學知識的自主性，并為終身學習打下良好的思維基礎。

如果教師能夠合理把握好數學知識的整體框架，并能結構化地設計教學過程，教學就不會淪為“粗暴的給予數學知識碎片”。當我們站在學生的角度幫助學生在學習的過程中邊學邊“串”，將數學學習整體化，最終學生得到的不僅是數學“知識鏈”，更多的是數學思維能力、學習能力的提升。當結構化教學的滲透成為一種自覺時，必然能改變教師的思維方式，激發學生的強大學習動力，進而發展學生的數學核心素養，讓學生的思維走向自主建構的結構化，為學生的終身發展奠定堅實的基礎。