數學建模和數學實驗在工科研究生“數值分析”教學中的融合和實踐
宋顯華 李冬梅 劉鳳秋

摘要:為提高工科研究生分析、解決數值計算問題的能力,文章研究了在“數值分析”課程教學中融入數學建模的思想和數學實驗的教學法。該教學思想通過數學建模過程引入數值案例,通過對基于計算機仿真軟件的數值案例設計過程進行描述、再現及討論,可以在短時間內增加授課信息量,激發學生學習興趣。從教學效果看,學生能夠較快地掌握常用數值分析算法,并能快速進入課題,收到良好的教學效果。
關鍵詞:數值分析;數學建模;數學實驗;教學改革
一、引言
“數值分析”是為我校機械工程、電氣工程、材料工程和化學與環境工程等專業的碩士研究生開設的一門學位課程,通常需要學生在本科階段學習過“高等數學”“線性代數”及“常微分方程”三門課程。“數值分析”課程又為后續的“數學模型”“軟件工程”和“算法設計與分析”等課程奠定知識和方法論基礎。該課程涉及內容較多,并具有很強的理論性和實踐性。隨著現代計算機技術的迅猛發展以及社會對碩士人才培養提出的更高要求,如何采用有效的教學方法,提高教學質量已成為“數值分析”課程教學任務中不可回避的重要問題。為了培養和提高學生發現、分析以及解決問題的能力,為今后能夠順利擔負科研任務打下堅實的基礎,根據該課程的特點,融入數學建模和數學實驗的教學法,不僅可以激發學生的學習興趣,使其對教學內容掌握得更加扎實,講解和實踐的案例還可以成為學生在將來從事科研活動時的重要參考資料。
二、“數值分析”課程的特點
國內外為碩士生開設的數值分析理論及類似課程所采取的講授方法基本類似。教學模式或者較為注重計算公式的推導,或者偏重于具體算法的應用。從教學方式上看,傳統的“注入式”教學模式仍占主導地位,這嚴重影響了研究生的個性培養、創新思維的訓練。總體來說,該門課程的特點可以概括為以下兩點:(1)具有理論數學的抽象性與嚴密科學性;(2)應用的廣泛性與實踐的高度技術性。
三、融合數學建模和數學實驗教學法的內涵與實例
(一)教學法的內涵與作用
結合“數值分析”課程教學的特點,可以作出如下定義:融合數學建模和數學實驗教學法是指在教師的策劃和指導下,基于教學創新理念,以提高學生分析解決問題的能力為目的,并以數值分析課程的知識結構為主線,組織學生通過對具有代表性的數值分析模型的提出、原理的解釋、應用領域的分析、思考、討論和交流等活動,引導學生自主探究,加深對知識理解等的一種特定的教學方法。
該教學法是一種理論聯系實際,啟發式的教學過程。通過教師采用數學模型引導來說明理論知識,通過實驗仿真,激發學生的學習興趣,提高學生分析解決問題的能力。采用該教學法可以克服傳統教學中“教師主體”的模式缺點,使學生成為教學的中心,不僅不必強記定理公式,而且能夠使學生了解到實際問題的多選擇性和不確定性,激發學生的創新精神。
目前,我校進行了研究生培養模式的改革,提高了要求,在這種情況下,傳統的培養方式及教學方式必須進行改革,該教學法具備上述優點,是一種非常適應現代教學現實的方法。
(二)教學法的實例
目前的數值分析理論課程教學,只是在分析已有的模型,而對于模型的提出過程講授得較少,因此造成了學生的分析能力強于綜合能力。而學生在未來的科研工作中,對于綜合能力的要求要高于分析能力。所以講授數值分析模型的提出過程對培養學生的綜合能力是十分有益的。在此筆者列舉教學實踐中的典型例子說明該教學法的優點。
應用實例:
在講授教材中“常微分方程初值問題數值解法”這部分的內容時,教材上只是給出了微分方程的幾種數值方法及其對應的誤差估計、收斂性和穩定性,內容較為晦澀難懂,學生往往不能理解常微分方程來自于哪些實際問題,特別不理解數值解的內涵,于是筆者在講授該部分內容時融入了數學建模的思想。為使學生理解數值解的內涵,借助C++、MATLAB或MATHEMATICA等軟件做程序的編寫,完成數值解的求解及幾種方法解的圖形顯示,加深對該部分內容的認識和比較。
提出數學建模問題:食餌捕食者問題。
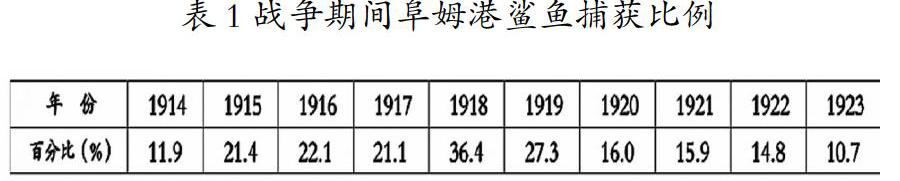
意大利生物學家DAncona發現:第一次世界大戰期間意大利阜姆港捕獲的鯊魚的比例有明顯的增加,如表1所示。
事實上,捕獲的各種魚的比例代表了漁場中各種魚的比例。戰爭中捕獲量會下降,而食用魚會增加,以此為生的鯊魚也同時增加。但是捕獲量的下降為什么會使鯊魚的比例增加,即對捕食者更加有利呢?
他無法解釋這個現象,于是求助于他的朋友,著名的意大利數學家Volterra。Volterra建立了一個簡單的數學模型,回答了DAncona的問題。
模型假設:
1.食餌增長規律遵循指數增長模型,相對增長率為r;
2.食餌的減小量與捕食者數量成正比,比例系數為a;
3.捕食者獨自存在時死亡率為d;
4.食餌的存在使捕食者死亡率的降低量與食餌數量成正比,系數為b。
通過上述教學案例的使用,使學生在學習常微分方程問題數值解的理論后,對一些實際問題,能夠建立微分方程組模型,并動手實驗給出方程組的數值解,加深對數值解的認識,對數值解收斂性、誤差情況和穩定性有具體的認知,并進一步通過圖形等方法對結果進行驗證、解釋和分析。
通過3個教學循環的教學經驗和多年的科研實踐經驗,如果采用新教學法,可以顯著提高教學效果,并且可以引入現代科研領域的一些前沿內容,推動教學改革的進行。
在數值分析理論課程的教學活動中引入了數學建模和數學實驗的教學法,對教學內容及實踐活動進行了總結,教學實踐活動表明該教學法能夠提高學生的獨立思考能力,解決問題的能力,使學生在理論知識和實踐能力方面達到了學以致用的效果,教學質量得到了明顯提高。
參考文獻:
[1]趙景中,吳勃英.關于數值分析教學的幾點探討[J].大學數學,2005,21,(3):28-30.
[2]李大潛.將數學建模思想融入數學類主干課程[J].中國大學教學,2006,28,(1):9-11.
[3]朱曉臨.關于差商和Newton插值公式教學的一些體會[J].大學數學,2010,26,(2):17-20.

