工欲善其事必先利其器

王學勝

【摘要】 數學思想方法是數學基礎知識的重要組成部分，教材中雖然沒有專門的章節介紹它，但是它伴隨著數學基礎知識而衍生和發展起來的，在數學中它是精髓，更是解題的指導思想. 本文將結合筆者的教學實踐和經驗來談談初中數學中主要數學思想與數學方法的應用，內容和觀點僅供大家參考.

【關鍵詞】 初中數學；數學思想；數學方法；應用

正文：

一、初中數學常見數學方法的應用

初中數學常見數學方法有多種，接下來，筆者將介紹幾個重點的方法來介紹.

1. 換元法

換元法的內涵：

所謂換元法，就是把某個式子看成一個整體，用一個變量去代替它，從而使問題得到簡化. 換元的實質是轉化. 另外，換元法的關鍵是能發現具有共同結構特征的式子，然后用一個字母表示它.

2. 配方法

配方法的內涵：

初中數學里的配方，就是把一個二次多項式的某些項配成一個或幾個完全平方式. 它的步驟是先化二次項系數為1，然后，加上并減去一次項系數一半的平方.

3. 待定系數法

待定系數法內涵：

在給出的或設出的某些式子中常常含有一些等待確定的（未知的）參數，在解決某些問題時，我們常常可以將這些未知的量當成是已知量去應用公式、建立方程，從而求出這些量. 這種方法就叫待定系數法.

待定系數法具體應用時常常分兩步：一是設出含待定系數的式子；二是應用公式或列方程求出待定的系數.

例3 已知，二次函數的圖像過（3，0），（2，-3）兩點，并且以x = 1為對稱軸，求這個二次函數解析式.

二、初中數學常見數學思想的應用

1. 分類討論思想

分類討論思想概述：

在解答某些數學問題時，有時會遇到多種情況，很難從整體上加以解決. 這時需要對各種情況加以分類，并逐類求解，然后綜合得解，這就是分類討論. 分類必須有一定的標準，標準不同，分類的結果也就不同. 分類的關鍵是要做到不遺漏，不重復. 需要分類的原因是“不確定”，引起“不確定”的根源常常有以下一些情況，具體包括：字母取值的不同導致運算結果不同；位置關系的不同導致圖形結構不同；對應關系的不同導致討論結果不同.

分類討論思想的應用：

2. 數形結合思想

數形結合思想概述：

數形結合是把抽象的數學語言與直觀的圖形結合起來思索， 通過“以形助數”或“以數解形”使復雜問題簡單化，抽象的數學問題直觀化、生動化，能夠變抽象思維為形象思維，有助于把握數學問題的本質.

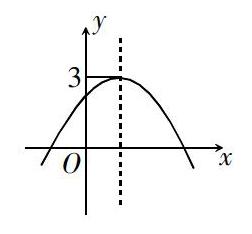
分析 如果根據b2 - 4ac 的符號來判別解的情況，本題將無從入手，可將原方程變形為ax2 + bx + c = 0，從而理解成是兩個函數的交點問題，即y = ax2 + bx + c，y = k.

由圖像可知只要y = k < 3就一定與拋物線有兩個不同的交點.

結 論

在初中數學教學中，各個版塊的知識與教學并不是孤立的，毫無聯系的，數學思想將這些看似碎片化、孤立的知識與版塊融為一體，相互聯系，相互運用. 無論是在哪個基礎教學階段，數學教學中的思想是潛在的一條長線，它于無形中指引著中學數學各個版塊的知識構架，并為許多問題的解答尋找到一個嶄新的突破口. 因此，在日常的數學教學中，我們要注重許多數學方法如換元、配方法，待定系數法等的使用，以及數形結合、化歸等思想在解題中的運用. 只有將這些思想領會于中，并融會于日常教學中，才能在教學與解題中發揮強大的力量，攻克疑難，占領先機！

【參考文獻】

[1]許敏.小學數學教學中滲透數學思想方法例談[A]，江蘇省教育學會2006年年會論文集（理科專輯）[C]，2006年.

[2]王振新.滲透數學思想掌握數學方法的重要性[J]，成才之路，2008年.