簡述初中數(shù)學數(shù)形結(jié)合教學策略

鄢玲

【摘要】 初中是學生學習數(shù)學的關(guān)鍵階段之一，相對于小學數(shù)學的內(nèi)容，初中數(shù)學難度增加，知識范圍也更大，學好初中數(shù)學也是學習高中數(shù)學的基礎(chǔ). 對于初中生來說，選擇正確的學習方法，能夠有效培養(yǎng)數(shù)學學習能力和數(shù)學思維. 對于初中數(shù)學教師來說，可以適當?shù)倪\用數(shù)形結(jié)合的方式開展教學. 本文將就初中數(shù)學數(shù)形結(jié)合教學策略展開探討.

【關(guān)鍵詞】 初中數(shù)學；教學方法；數(shù)形結(jié)合

引言：數(shù)學是一門邏輯性較強的學科，數(shù)學研究的主要內(nèi)容是空間形態(tài)和數(shù)量關(guān)系等，數(shù)學學科包括了數(shù)和形兩個大概念，要提高解題速度和解題正確率，就要將數(shù)和形兩個概念恰當?shù)慕Y(jié)合起來，教學中也要將數(shù)形結(jié)合作為一種重要的方法傳授給學生.

1. 數(shù)形結(jié)合思想簡介

從字面上看，數(shù)形結(jié)合就是將圖形和數(shù)量結(jié)合起來，運用其中的關(guān)系解決問題，將抽象和復雜的數(shù)量轉(zhuǎn)化為具體和簡單的圖形，這樣更加直觀和形象，便于解決問題. 一些題目也需要把數(shù)量關(guān)系轉(zhuǎn)化為圖形來分析和解決，數(shù)形結(jié)合思想的核心就是數(shù)量和圖形的相互轉(zhuǎn)化. 在初中階段，學生的抽象思維還不是很強，因此運用數(shù)形結(jié)合的思想解決問題是一種非常重要的方式，也能夠培養(yǎng)學生的數(shù)學思維能力，最重要的就是變抽象為具體，變繁瑣為簡單，提高解題效率和正確率，幫助學生樹立學好數(shù)學的信心，消除對數(shù)學的厭煩和畏懼心理，提高數(shù)學成績，對于教師提高課堂教學效率也有很大幫助.

2. 數(shù)形結(jié)合思想的重要作用

數(shù)學是一門抽象性較強的學科，并且還有形式化和符號化的特點，理解數(shù)學知識和概念可能存在一定難度，再加上解決數(shù)學問題一般需要復雜的邏輯推理，因此很多學生不喜歡數(shù)學甚至厭煩和恐懼. 而教師一般只是傳授理論知識，對于學生是否聽懂、是否能夠解題不甚了解，反復強調(diào)單一的邏輯思維，卻不運用圖形的方法幫助學生更好的理解抽象的數(shù)學概念. 實際上教材中就包含了大量的數(shù)形結(jié)合思想，在教學過程中教師可以恰當?shù)倪\用，揭示數(shù)學的本質(zhì)，減輕學生學習數(shù)學的負擔.

3. 數(shù)形結(jié)合思想在初中數(shù)學中的應用

3.1 以數(shù)化形的應用

在初中數(shù)學中，一些數(shù)學知識和數(shù)學關(guān)系較為抽象，學生理解可能存在一定困難，而圖像能夠形象、直觀的表達信息，可以將抽象的關(guān)系、知識變得具體. 在初中階段，以圖形來代替數(shù)量主要有兩種方法，也就是采用平面幾何或者解析幾何的方式. 以數(shù)化形的優(yōu)點是：采用簡單直觀的數(shù)學圖形，不需要大量的計算或者推理，更容易理解數(shù)學中晦澀難懂的概念和關(guān)系，取得良好的學習成果. 例如在講授平方差公式這一概念的時候就可以運用數(shù)形結(jié)合的方法，首先計算多項式相乘：（m + 2）（m - 2）、（2x + 1）（2x - 1），得到結(jié)果后進行比較，分析兩個結(jié)果與算式的關(guān)系，找到其中的規(guī)律，然后計算（a + b）（a - b），得到平方差公式，再結(jié)合圖形分析平方差公式的內(nèi)容，了解平方差公式的幾何意義.

3.2 以形化數(shù)的應用

圖形具有直觀易懂的優(yōu)點，但是無法表示定量，因此還要結(jié)合代數(shù)計算才能實現(xiàn)定量. 對于一些圖形，不論是復雜的還是簡單的，單單靠觀察可能很難找到規(guī)律或者得到結(jié)論，因此還要結(jié)合數(shù)量來分析，挖掘圖形中包含的隱含條件，利用數(shù)量關(guān)系解決圖形問題. 例如在講解角平分線這部分知識時，教師首先向?qū)W生介紹平分角的儀器，引導學生使用尺規(guī)作出角平分線，然后讓學生通過折紙的方式自己找出角平分線，教師應引導學生觀察紙張上折痕的數(shù)量和長度，最后總結(jié)角平分線的定理和性質(zhì)，但是教師仍然需要進行推理和證明.

3.3 數(shù)形互變的應用

解決一些數(shù)學問題有時單單依靠上述兩種思想是不夠的，需要將以形化數(shù)和以數(shù)化形兩種方法結(jié)合起來. 例如在講解函數(shù)與平面直角坐標系的知識時，教師應告訴學生坐標系除了可以表示地理位置，還可以在直角坐標系中架設一座“橋梁”，橋梁上的每一點都與平面上的有序數(shù)對（x，y）對應，將函數(shù)與直角坐標系結(jié)合起來.

3.4 數(shù)形結(jié)合思想在函數(shù)中的應用

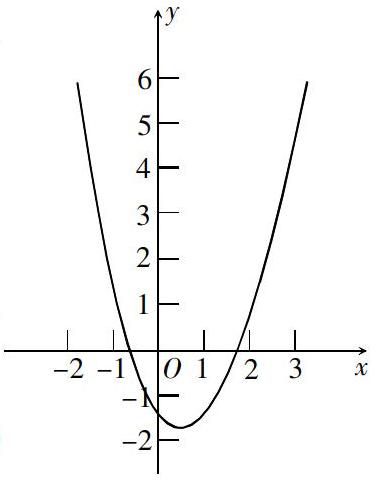
初中數(shù)學中函數(shù)是重點內(nèi)容也是難點之一，其中的二次函數(shù)是學習高級數(shù)學的基礎(chǔ)，因此采取數(shù)形結(jié)合的思想進行學習是非常重要的. 例如：如果關(guān)于x的方程x2 + 2kx + 3k = 0有兩根，并且都在3和-1之間，那么k的取值范圍是多少？對于這道函數(shù)問題，可以設f（x） = x2 + 2kx + 3k，結(jié)合下面的圖像 ：

可得f（-1） > 0，f（3） > 0，f（-k） < = 0，也就是2（-1） + 2k（-1） + 3k > 0，32 + 2k·3+3k > 0，（-k）2 + 2k（-k） + 3k < =0，可以解得k > =3或-1 < k < = 0.

3.5 數(shù)形結(jié)合思想在應用題中的應用

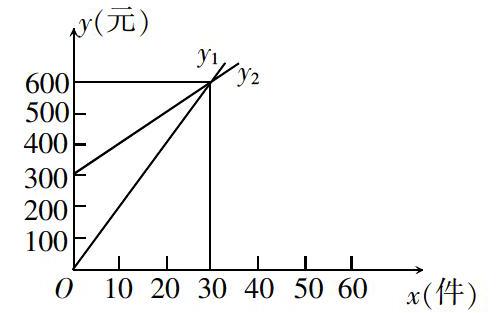
應用題分值較高，考察的是學生的綜合能力，學生解決問題時可能會遇到困難，在應用題中采用數(shù)形結(jié)合的方法解題，能夠大大提高解題效率，提高解題正確率. 例如：一公司生產(chǎn)新產(chǎn)品，推銷數(shù)量為x，推銷費用為y，根據(jù)下圖回答問題：（1）y1和y2的解析式為？（2）圖中兩種方案如何付推銷費？

解：（1）解析式為：y1 = 20x；y2 = 300 + 10x；（2）y1不需要推銷因此無推銷費，推銷十件可得推銷費200元；而y2有300元保底工資，推銷十件可得100元提成.

結(jié)束語

綜上，在初中數(shù)學中不論是教學還是學習，都滲透著數(shù)形結(jié)合的思想，恰當?shù)倪\用這種思想，能夠提高解題效率和正確率，改善教學效果.