立足單元整體教學 構建有效數學課堂

金浩

摘要：單元整合運用的是“整體——部分——整體”的教學方式，采用“見樹木，更見森林”的理念，對一個知識點多且相對零散的單元進行整合，建立知識間的聯系，讓學生在學習過程中認識并體會各部分之間的相互聯系與區別，達到熟練掌握、靈活運用知識的目的。在教學實踐中，尋找單元整體教學內容的契合點，并實施有效的實施策略。

關鍵詞：單元整體教學；契合點；有效策略

中圖分類號：G633.6 文獻標識碼：A 文章編號：1992-7711（2016）06-0108

作為一名一線初中數學教師，筆者經常發現一些孩子數學單節作業不差，但單元檢測不行；一些孩子學一節忘一節；一些孩子各知識點都清楚，但不會列單元知識提綱；單一知識點可行，綜合一章內容不會……

現象表明，學生按照教材安排的“一課一學”“逐課推進”的教學模式學習，一定程度上隔斷了前后知識的關聯性，喪失了單元的整體意識。于是，筆者開始了單元整體教學的設想和初步研究。

一、實施單元整體教學的內容契合點

1. 整體模塊的相似性

初中幾何源于小學幾何，在小學時期，學生通過觀察、操作對許多圖形已經有了一定程度上的感官認識。學生對每個圖形都有整體感覺卻缺少系統的學習。

至初中以來，學生要依次學習線、角、三角形、四邊形、圓、直棱柱、圓錐等，對幾何的學習是從簡入繁、從易到難。其中，我們可以發現三角形與四邊形其實同屬于多邊形中的一塊知識，那么把三角形和四邊形分別看成是一個整體模塊的知識，對其進行整體學習。以三角形的知識點框架為起點，四邊形知識點框架為落點，而連結起起點和落點的是知識模塊的相似性。

2. 知識結構的相似性

初中階段三角形的學習內容包括定義、相關概念、性質、整體性、特殊化這四個方面。那么，學習四邊形的內容也可以從這四個方面用類比的方法進行學習。

如浙教版八年級下冊第四章《4.1多邊形》：

（1）我們學過哪些幾何圖形？（引導學生從點、線、面、體4個方面進行回顧，回憶線段、一般三角形和特殊三角形、一般四邊形和特殊四邊形、圓等幾何圖形，讓學生感受幾何內容的整體輪廓。）

（2）至初中以來，我們已經系統的學習到哪個幾何圖形了？你覺得我們接下來應該研究哪個幾何圖形呢？

（3）三角形與四邊形都是由不在同一條直線上的線段首位順次連擊構成，這樣的圖形我們統稱為多邊形。它們既然同屬于多邊形，那么我們是否可以以學習三角形的方式去研究？

（4）回憶以往，我們研究了三角形的哪些知識？（初步形成框架）

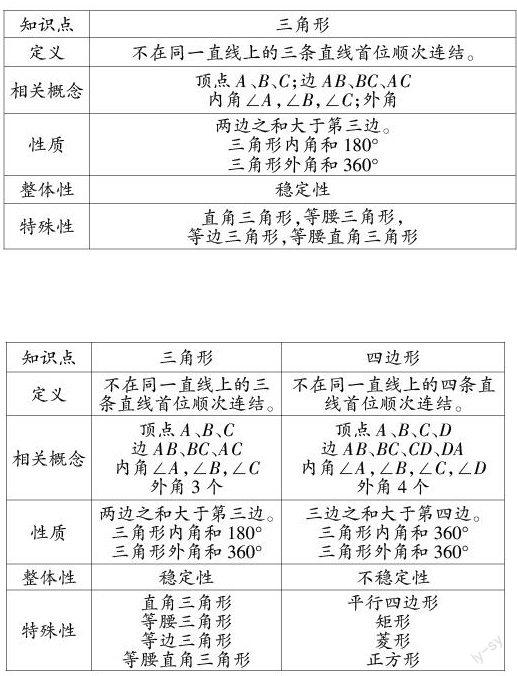
通過這四個問題，引導學生對三角形知識的回顧和對四邊形知識的展望。讓學生形成整體知識的框架（如右表），為四邊形的學習打下基礎。

利用三角形的整體框架，從這幾個方面去研究四邊形。（擴展形成新知）

【效果分析】這樣用一節課的時間讓學生對整個四邊形的知識系統形成框架，先有一個整體概念，然后對整體進行剖析，采用討論——展示——總結的學習方式，通過猜想——實驗——驗證的學習方法，對模塊中的細節進行填充。讓學生先知道自己要學什么，怎么學，再體驗自主學習的過程。采用這樣的整體——部分——整體的整體教學模式，比按教材中安排的分割教學更能讓學生知道學習的出發點和目的性（從哪里來，又要到哪里去），形成知識點的整體框架，并以此習得方法，用整體性的思維和角度運用于學習及生活的方方面面。

3. 研究角度的相似性

三角形和四邊形都是由線段構成的圖形，那么它們所要研究的角度也具有很高的相似性，都可以從邊、角、線、整體感觀性這四個方面為切入口對其進行整體教學。

如浙教版八年級下冊第四章《4.2平行四邊形及其性質》中，平行四邊形與特殊三角形的性質比較：

【效果分析】用整體教學的方式，為學生的自主、合作探究指引了方向，用整體思維和角度而有目的地去有效臆想、去深入探究。

4. 整體模塊的連貫性

人們在對生活應用時發現，當有理數不夠用時，把有理數域擴充到實數域；當數的變化有了規律時，就用代數式表示這種規律；而代數式中的字母數值的變化帶動了代數值的變化，就有了函數；當函數值特定或處于某一數域時，要研究字母數值，就有了方程和不等式，這些就形成了初中階段的代數體系。其中研究函數、方程和不等式的基礎就是代數式，而代數式又包括整式、分式、根式等。那么，在此之中具有整體連貫性的知識，可以用整體教學的方式進行，以達到知識模塊的整體遷移的目的。比如，在整式內容中，整式乘法和因式分解是一個互逆的過程，是一個代數式的兩種表達式的相互轉化，把兩者都看成一個整體，進行整體學習。那么，我們以整式乘法為起點，以因式分解為落點，而連結起點與落點的是逆轉等式左右兩邊。

（1）計算：當a=101，b=99時，a2-a×b=

當a=101，b=99時，a2-b2=

當a=101，b=99時，a2-2a×b+b2=

以化解計算繁瑣的需求引導學生進入“把一個多項式轉化成整式乘積的形式”的思考。

用一個具體例子，讓學生感受到有時候因式分解可以簡化問題，讓他們體驗這種神奇的過程，對其產生需求性，激發了濃厚的學習興趣。

（2）分解方法提煉：

設計：你能否將下列多項式轉化成整式乘積的形式？并說明各多項式特征和轉化過程。（提示：利用整式乘法運算嘗試檢驗。）

①6a3b+9a2b2-3a2b

②4a2-9b2

③4a2-12ab+9b2

④2a3+12a2b+18ab2

⑤a2+a-6

⑥3a+ab+2b+6

通過整理比較，總結出因式分解的幾種類型及多項式特征：

①提取公因式法，特征：每一項都含有相同的因式。

②平方差公式，特征：（△）2-（□）2。

③完全平方公式，特征：（△）2-2（△）（□）+（□）2。

④多次分解，特征：①②或①③可以先后進行兩次分解。

⑤十字相乘法，特征：x2-（a+b）x+ab的形式。

⑥分組分解法，特征：（△）（□）+（△）（○）+分組后形成的形式。

目前先來學習幾種簡單的①②③④形式

【效果分析】用該種合作討論學習方式，讓學生放開思維的桎梏，自尋發現因式分解的多種多樣，了解因式分解整體框架其實很寬廣，只是我們目前只學習其中的一部分，借此也可以提高學生思維的廣度，有利于學生素質的提升。當然⑤⑥這兩種分解法留給學有余力的學生進行探究，可在課內不深究和展開，留到課外以供學生學習，提高學生的學習興趣。

二、實施單元整體教學的有效策略

1. 借用表格，構建知識的橫向對比

著名教育家烏申斯基認為：“比較是一切理解和思維的基礎，我們正是通過比較來了解世界上的一切的。”初中數學中各個知識點既有聯系又有區別，在教學中充分運用知識點橫向對比的方法，有助于突出和突破教學難點，使學生容易接受新知識，防止新舊知識的混淆，提高辨別能力，從而扎實地掌握數學知識、發展邏輯思維能力。

在學習反比例函數時，筆者制作一次函數與反比例函數的對比圖表，通過兩者在函數式、圖像、與坐標軸交點和性質等方面的對比，凸顯二者的區別，讓學生能夠通過它們的差異性，更透徹地理解反比例函數本身所具有的特性。同時，引導學生進行學法遷移，可采用知識的橫向對比法區分相關知識，在對比中不斷培養學生的思維能力和分析問題、解決問題的能力，在比較中掌握解題方法。

2. 借用框架圖，理清知識點的縱向聯系

在教學《一元二次方程》時，通過框架圖，將整個初中階段方程的知識框架以圖示的方式展現給學生，讓學生感受一元二次方程在整個方程系統中所處階段和地位以及它的形成和由來。同時，我們也可以利用該框架圖，讓學生感受類比和轉化的思想：（1）相同類型的知識可以通過類比的方法構建，如一元一次方程研究概念、解法、應用這三方面，而一元二次方程也從概念、解法、應用這三方面進行研究；（2）新問題可以溝通舊知識，通過轉化的思想轉化為舊問題進行解決，如一元二次方程的求解可以轉化成一元一次方程進行解決。

三、結語

在新課程改革中，我們積極踐行新課改精神，充分挖掘教材、從學生實際出發，大膽探索、勇于創新、樂于實踐，積極探索初中數學單元整體教學，樹立學生“見樹木，更見森林”的整體性學習意識，構建有效的數學課堂，全面提升學生的數學素養，促進每一位學生的健康發展。

參考文獻：

[1] 向 垚，張 梅.淺談初中數學單元整體教學可望可即的對策[J].新課程（中學），2015（1）.

[2] 歐陽紅波.單元整合、整體推進法在整式的乘除教學中的嘗試[J].數學學習與研究（教研版），2015（21）.

[3] 楊顯攀.“整理課”：讓學生在整理中學會學習[J].中小學，2015（4）.

（作者單位：浙江省溫州市第十七中學 325000）