初中數學教學中“問題導學法”新探
郭媚
摘 要:初中數學新課程標準倡導學生通過“自主、合作、探究”式地學習,實現知識、能力,情感態度與價值觀的三維目標。“問題導學法”便是落實新課程標準的有效教學方法。實施此法要把握好“問題”、“導”、“學”三個要素:問題--注意角度、難度、廣度、密度;“導”--創設情景加以引導,循循善誘進行疏導,不厭其煩給予輔導;“學”--形成學習模式.其次,“問”“導”“學”要有機聯系。
關鍵詞:新課標;問題導學;有機聯系
中圖分類號:G632 文獻標識碼:B 文章編號:1002-7661(2016)14-353-01
新課程改革強調改變過去“知識本位,螢視結論性知識,輕視過程性知識形成過程”的做法,倡導學生通過“自主、合作、探究”式地學習,實現知識、能力、情感態度與價值觀的三維目標。“問題導學法”便是落實新課程目標的有效教學方法之一。筆者在近幾年的教學實踐中,對“問題導學法”進行了一些有效的探索,現將一些體會交流如下:
一、以問導學,要把握好三個要素
“問題導學法”是指在建構主義理論、多元智能理論指導下,把教學內容轉化為有價值的、值得探究的、有多種解決方法的科學問題,在教師的引導、疏導、輔導下,創造條件讓學生自主、探究、合作學習。運用該方法進行教學,要把握好!“問題”、“導”、“學”三個要素。
1、“問題”是基礎:古語云“學起于思,思起于疑”,問題是思維的起點,也是學習的動力源泉。設計有探究價值的問題是實施“問題導學法”教學成功的基礎。為了保證問題的“探究性”,要注意以下“四度”:選好角度,以能激發學生的興趣;把握難度,以達“跳一跳,摘得到”效果;體現廣度,以使面向全體學生;控制密度,以求保證思考時間。如初二“分式加減法”中異分母分式加減法的教學:我先讓學生思考和分組討論:①異分母分式相加減要先做什么?(通分)②如果分式的分母是多項式,要先做什么?(將分母分解因式)③怎樣確定最簡公分母?④要通分,各分式的分子和分母分別乘以什么?⑤通分后如何進行加減?以上問題學生對照例題一個個思考后教師進行釋疑,再要求學生做練習。問題的出現自然而然,富有邏輯性、層次性,解決問題所需的思維水平處于學生“鄰近發展區”,學生通過探究后有能力解決問題,有效地引導了學生的學。
2、“教師的導”是關鍵:新課程理念提倡以學生為中心的主體教學,但這并非意味若教師就顯得無足輕重了。主體性教學強調學生的主體地位,又不忽視教師的主導作用。“問題導學法”下學生的“學”也是依靠教師的“導”來進行,教師是否能最大限度地發揮主導作用,直接影響著學生主體地位的發揮。筆者認為,教師應做好以下三“導”:
(1)創設情景加以引導:筆者常常要求學生就生活中與數量有關的問題寫成數學問題交我整理,把寫得好的在課堂上展示,讓同學們探究問題答案,體驗數學的價值。面對起源于現實生活的問題,學生表現出濃厚的興趣,由此引發相關的探究。如進行積的乘方運算時,提出問題:現有邊長為a的正方形紙片若十個,用多少張邊長為a的正方形紙片能拼成一個新的正方形?并用不同有法表示新正方形面積,你會有何發現?學生畫出了圖形,經過互動探究,學生討論得出了結論。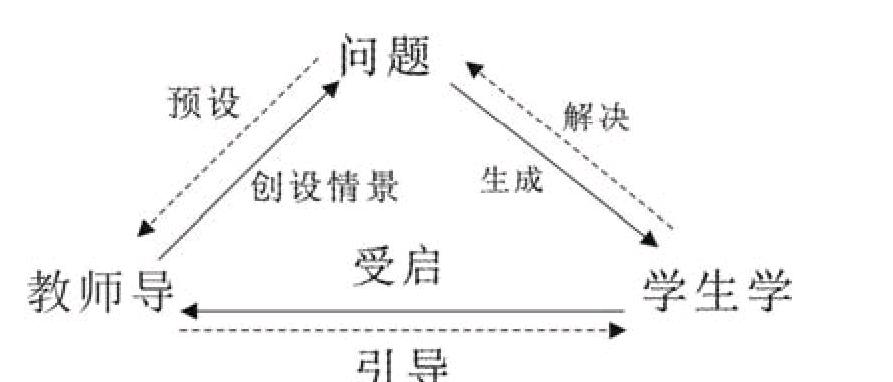
(2)循循善誘進行疏導:在進行同底數冪的乘法??.??運算教學時提問:①這是什么運算?(乘法)②參加乘法運算的對象是什么?(冪)③這些冪有何特征?(底數相同)④怎樣運算?(底數不變,指數相加)在循序漸進的誘導下,學生有了解決問題的自信心。
(3)不厭其煩給予輔導:不同學生存在著基礎差異,教師應特別關注基礎相對薄弱的學生,給予他們及時輔導。
3、“學生的學”是核心:“問題導學法”教學應強調將學生從回答問題的“被告者”轉變為解決問題的“主體參與者”,從向保證“學生的學”的課堂核心地位。為此,在基于問題的教學中可以將以上二種學習方式進行如下圖1所示的有機組合,從而更有效地發揮它們的優勢,使問題得以有效解決。
二、“問”“導”“學”要有機聯系
“問”導“學”要有機聯系,構建起不同層次的“問題導學”。“問題導學法”的實施,其三大要素——“問題”、“導”、“學”具有各自不同的地位,但是它們又并不是孤立的,而是相互關聯,構成一個有機的整體。具體又可以有如下兩種關聯方式(圖2):
1、教師通過提出預設問題引導學生學,這樣學生的“學”就是單純解決問題的過程。引導學生探究的方向,這是一種較淺層次的“問題導學”。
2、教師通過創設情境引導學生自己生成問題,然盾再嘗試解決問題。教師則是一步一步地引導學生自己提出對課題研究有價值的、值得探究的、有多種解決方法的細化問題。這樣學生的學不僅是解決問題的過程,還是發現問題的過程,動力自然更足了。顯然,這是一種較深層次的“問題導學”。在學整式時,關于(π-1)х?у是單項式還是多項式的討論中,教師提問:①1是單項式嗎? 3呢?1+3是單項式還是多項式?②x+x是單項式還是多項式?③(3 -1) a?呢?(x -1) a?呢?在完成以上提問后,學生自己得出,結論?形如(3 -1)a?,(π-1)a?y具體數與寧母的積的整式是單項式,但x+x、(x-l)a?是多項式。
綜上所述,學生帶著問題進入課堂,又帶著更多的問題走出了課堂。問題不是教師要求學生思考的,而是由學生們自己提出的,這樣學生學習的主動性才能真正得以發揮。學牛由此所養成的“提問”習慣將會終生受用。

