從余弦定理的證明看學生的發散思維
郭俊楠
河南師范大學數學與信息科學學院,河南 新鄉 453007
?
從余弦定理的證明看學生的發散思維
郭俊楠
河南師范大學數學與信息科學學院,河南新鄉453007
摘要:縱觀近幾年的數學高考試卷,我們發現對學生發散思維的考察越來越多,但學生具有較好的思維發散能力并不僅僅是數學的要求。在當今這個飛速發展的信息化時代,求異和創新愈發顯得彌足珍貴。所以,學生發散思維的培養和鍛煉一直是現代教學中的重點與難點。本文從余弦定理的證明出發,多方面、多層次地進行思考和分析,在探討多樣證明方法的同時,以尋求培養學生發散思維的策略。
關鍵詞:余弦定理;發散思維;求異;創新
何為發散思維?根據思維的指向性,思維可分為集中思維和發散思維。思維是人腦對客觀現實概括的和間接的反映,它體現的是事物的本質與內部規律性。發散思維也稱輻散思維、求異思維,是根據已有的信息,從不同角度思考,從多方面尋求多樣性答案的一種展開性思維活動。下面,我們就從余弦定理的多種證法看學生思維的發散性。
在數學中,用符號語言來描述余弦定理,即:a2=b2+c2-2bccosA ① b2=a2+c2-2accosB②c2=a2+b2-2abcos③
分析:余弦定理的公式中給出了四個量,“知三可求一”,因此,證明余弦定理即解決已知其中的三個量來表示另外一個量的問題。
思維取向一:解析法
在△ABC上建立直角坐標系,如圖1,點A為原點,點B落在x軸正半軸上,設三角形 三邊分別為a,b,c,則三點的坐標分別為A(0,0),B(c,0),C(bcosA,bsinA),已知BC=a,由兩點間距離公式可得:
化簡可得:a2=b2+c2-2bcosA
同理可得②③.
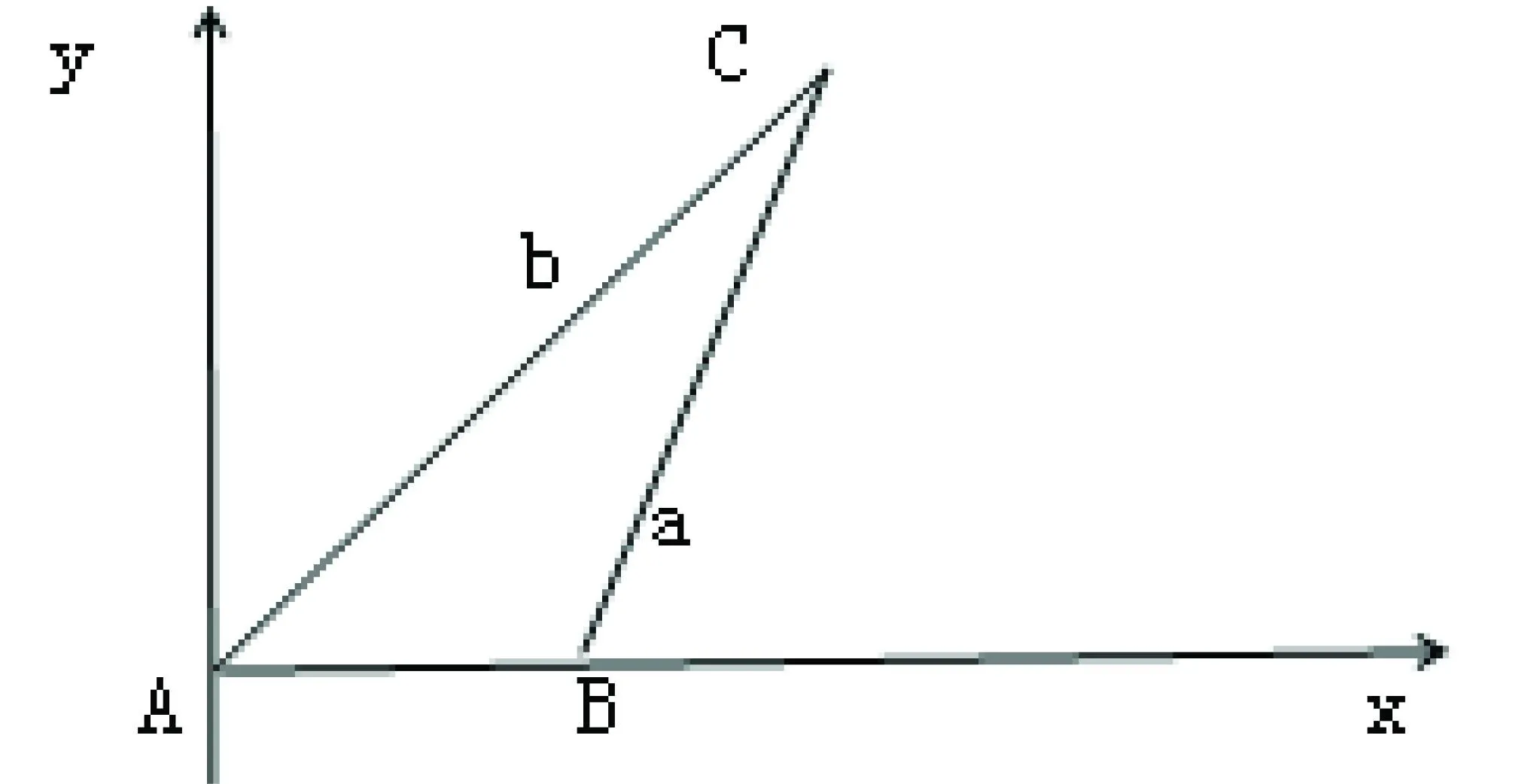
圖1
點評:此法是通過建立坐標系將幾何問題用代數觀點來解決。筆者認為這個方法簡單易懂,學生很容易就能想到求邊長也即求兩點間的距離,關鍵是要想到如何巧妙地建立直角坐標系(將一點放在原點,另一點置于x軸上)。
思維取向二:勾股法
在任意△ABC中,如圖2,AB=c,AC=b,BC=a過點A作邊BC的高AD,則由圖2可知 AD=cinB,CD=a-ccosB
在RT△ADC中,滿足AC2=AD2+DC2
b2=c2sin2B+a2+c2cos2B-2accosB
=c2+a2-2accosB
同理可得②③.
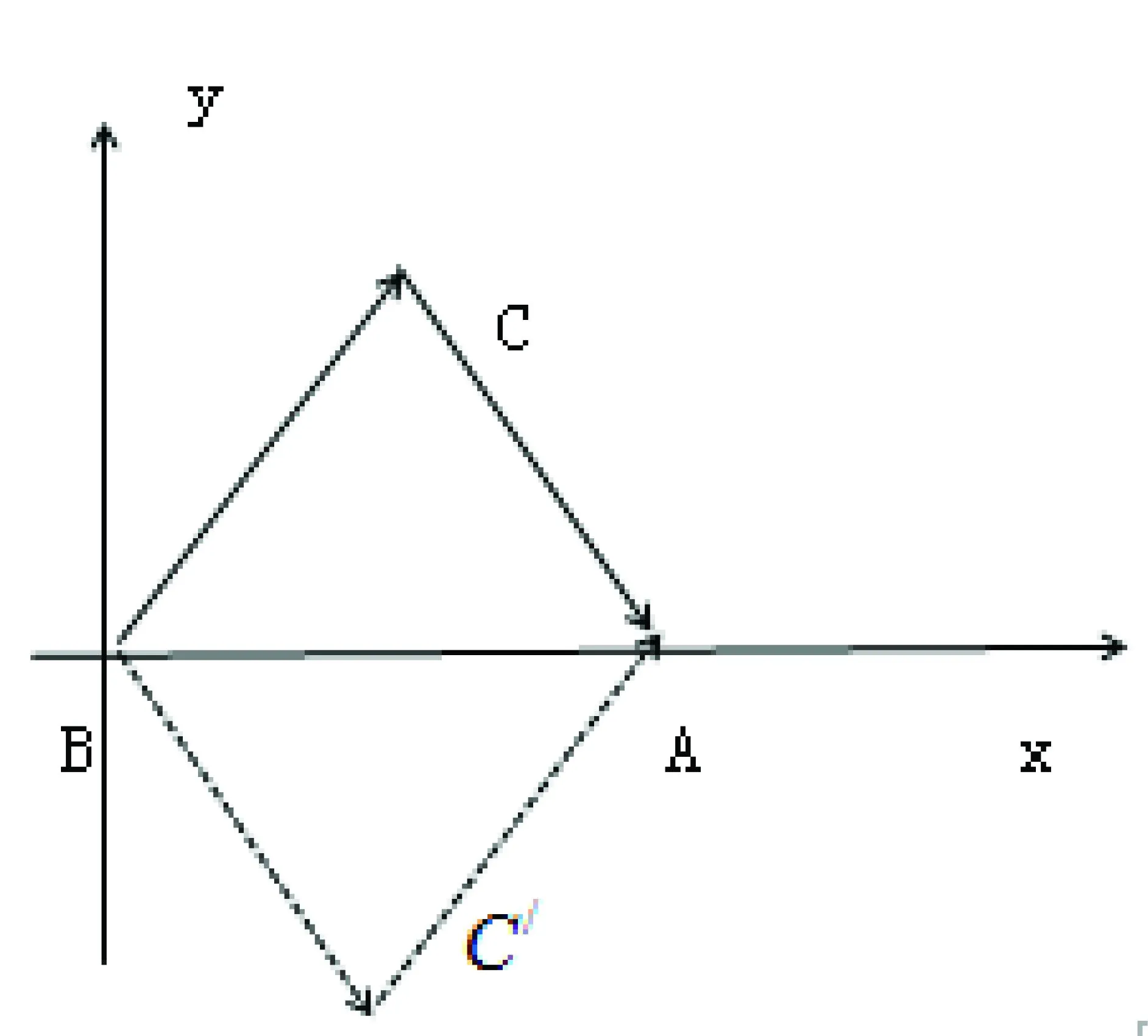
圖2
點評:筆者認為此方法相對前三種方法不管是在計算量上還是思路上都更為簡單。一開始我們接觸到的銳角三角函數是根據直角三角形中的銳角得到的,而余弦定理是適用于任意三角形,通過在任意三角形中構造直角三角形,恰當地運用三角函數將邊角關系有機的結合起來,即可得到余弦定理,其實,我們不難發現當一個角為直角時余弦定理即為勾股定理。
思維取向三:射影定理法
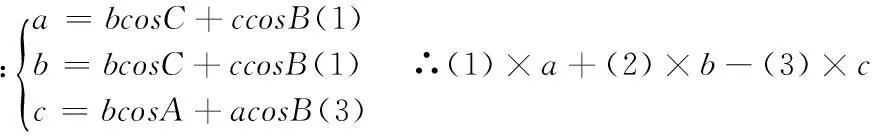
即c2=a2+b2-2abcosC
同理可得②③.
分析:余弦定理刻畫的是任意三角形邊角的關系,任意三角形的射影定理也涉及到邊長和角度,為了將兩者聯系起來進行了步驟*,稍加整理即可得到余弦定理。
思維取向四:復數法
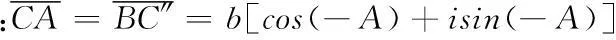
即:c=a(cosB+isinB)+b(cosA-isinA)=(acosB+BcosA)+i(asinB-bsinA)(*)
對等式(*)兩邊分別平方可得:c2=a2+b2-2abcosC,同理可得②③.
點評:此方法是上述向量法與解析幾何法的結合,不同之處在于此方法中的坐標系與計算均是在復數領域內。
這四種證法對于高中生來說并不難理解,在學生原有的認知結構為基礎之上,通過將新舊知識間建立聯系。但難的是如何針對一個問題從不同角度找到多樣的解決辦法。這就需要現代教師在教學過程中有意識地培養學生的發散性思維。
通過對余弦定理證法的思考與分析,并結合思維的一般品質,關于如何培養學生的發散思維我提出以下三點。首先應引導學生在學習中抓住事物的規律和本質,深入的思考問題,從而增加學生思維的深刻性,為思維的發散奠定一個良好的基礎。其次,鼓勵學生在學習中追求“標新立異”,勇于創新。因此,在教學過程中,可以根據學生的這種心理特點,鼓勵其大膽想象,嘗試突破思維的局限,從多角度、多層面思考問題。如復數法或許就很少同學能夠想到,因為大家都不約而同地將余弦定理限定在實數范圍,很少去想利用復數能不能解決這個問題;大多數同學也都認為用數學知識解決物理問題理所當然,而不會想到是否可以用物理知識解決數學問題。同時,作為教師應用包容與鼓勵的眼光看待學生在“求異”過程中出現的錯誤與失敗,并以恰當的方式幫助學生改正想法中的不足。當然,適當的有針對性的習題訓練對學生發散思維的培養也是必要的。結合教學內容和學生實際情況,采取多種形式的習題訓練,可激發學生求異創新的欲望,幫助學生養成多角度思考問題的習慣。
[參考文獻]
[1]孔凡哲,曾崢編著.數學學習心理學[M].第2版.北京:北京大學出版社,2012,5:197-203.
[2]徐英.用物理法證明正弦定理與余弦定理[J].中學數學雜志,2006.9.
[3]楊春茹.高中數學教學中培養學生發散思維的研究與實踐[D].中國知網數據庫.東北師范大學,2003.5.
[4]方炫蘇,方華平.余弦定理的幾個證明方法[J].中學生數學,2013.5.
中圖分類號:G633.6
文獻標識碼:A
文章編號:1006-0049-(2016)14-0194-01

