《參數方程復習》課例研究

張新華

（哈爾濱市第五十九中學 黑龍江哈爾濱 150030）

《參數方程復習》課例研究

張新華

（哈爾濱市第五十九中學 黑龍江哈爾濱 150030）

《極坐標與參數方程》是高中人教版教材選修4-4的主要內容， 在高考中考察的難度不大，學生容易入手。對于我們普通高中的學生來說，是能得分的。也是十分珍貴的。為此，我們備課組選擇了《參數方程復習》一課作為研討課。

在最初備課時，我想復習要全面。但是一節課的時間，內容太多學生不易接受。所以，我確定了復習的重點：直線的參數方程中t的幾何意義的運用以及圓錐曲線參數方程的簡單應用。為了能使這節課有實效性，我還向其他老師請教。這些老師的話讓我深受啟發：“教師通過引導，讓學生主動參與到學習活動中”“高三復習要面向高考，精選高考題作為例題……”這些老師耐心、細致、專業的指導，為我這節課的成功奠定了基礎。

下面是這節課的課堂實錄（節選）

一、創設情境

師：請大家觀察前面的兩個問題，在題設上有什么相通之處？

過點M（-1，2），與曲線C： y2= 4x 有兩個交點A、B 求：

判斷曲線C與直線 L的位置關系

生：都有圓錐曲線，都有直線的參數方程

師：都與參數方程有關，對于參數方程，大家都能提出什么問題？

生：什么是參數方程？，為什么學習參數方程？······

師：概括一下同學們的問題：

第一、什么是參數方程。第二、常見曲線的參數方程有哪些。第三、為什么要建立參數方程

設計意圖：通過問題引出本節課的主要內容，為本節課的學習指明了方向。

二、嘗試概括

什么是參數方程、常見曲線的參數方程（略）

三、探究歸納

師：看前面提出的問題：

過點M（-1，2），與曲線C： y2= 4x有兩個交點A、B

（3）

（4）線段AB的中點P的坐標

首先思考不用參數方程的知識該怎樣解？

生：聯立方程，求交點坐標，再求解。

師：學了參數方程后，又能怎樣解？

生：把直線的參數方程代入拋物線，求A、B兩點對應的參數

師：請同學們動筆計算，請一名同學到黑板運算。

與圓錐曲線交于兩點A、B，且A、B對應的參數分別為21,tt 則③線段AB的中點對應的參數

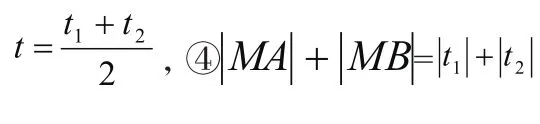
設計意圖：通過一道例題，把直線參數方程中t的幾何意義的運用的常見問題及解法進行歸納總結，對我們學生來說非常必要，有助于學生對知識的梳理與掌握。

師：再來看其它曲線參數方程的應用問題，怎樣解決?

直線x+2y-2=0，點P在橢圓上，求P到直線距離的最大值。生：利用橢圓的參數方程設點P的坐標P( )θθ sin2,cos3

師：再看下面的變式題，怎樣解？

生：設出點P的坐標，表示出2x+y

師：留作課后完成

師：通過這兩題，誰能總結一下求圓錐曲線上與動點有關的最值問題的一般做法？

生：圓錐曲線上與動點有關的最值問題，一般做法：

（1）寫出圓錐曲線的參數方程，把兩個變量轉化為一個變量。

（2）三角恒等變形，轉化為求三角函數最值問題。

（3）寫出最值、范圍等。

設計意圖：強調解題步驟，強化解題方法，為后面的例3做鋪墊。

四、應用提升

師：根據目前我們對參數方程知識的掌握，對下面的題設

你能提出什么樣的問題？生1： 相交求弦長……

生2：求橢圓上的點到直線的最大距離……

師：什么樣的問題選擇直線的參數方程來解，什么樣的問題選擇圓錐曲線的參數方程來解？

生：求弦長等問題用直線的參數方程來解，求最值問題選擇圓錐曲線的參數方程來解。

設計意圖：這個問題是開放性的，只有題設，學生自己提出問題。如果學生對前面的兩個例題掌握了，就能仿照例1、例2那樣提問。這既是對本節知識的檢驗，也是對本節知識的應用于提升。