基于貝葉斯網絡的流域內水文事件豐枯遭遇研究

呂振豫　穆建新　王富強劉姍姍

摘要：基于貝葉斯網絡理論結合Copula函數建立了東江流域上、中、下游三個站點降雨、徑流豐枯遭遇的風險管理模型，直觀地描述了各個站點間降雨、徑流的相互關系。利用Copula函數建立聯合分布模型計算了站點間不同豐枯組合狀態調水不利情況的風險概率。通過貝葉斯網絡結構的反向推理功能，以后驗知識作為輸入，進一步對流域內未來調水可能面臨的豐枯遭遇情況進行了仿真計算。結果表明，系統中一個節點的變化將會對其他節點的概率值產生巨大影響，以上、中游降雨為枯水情況作為后驗輸入，站點間豐枯遭遇調水不利風險概率增幅至55%以上；仿真結果可以為流域內調水方案的制定提供理論支撐。

關鍵詞：東江流域；Copula函數；貝葉斯網絡；豐枯遭遇；風險分析

中圖分類號：P333.9；X820.4 文獻標志碼：A 文章編號：

16721683（2016）05001808

水文事件豐枯變化的差異性及不確定性，直接影響流域內調、受水的可控水量，對工程調水風險、流域水資源配置產生重大影響。近年來，不同區域水文事件的豐枯遭遇問題引起了廣泛關注[14]，分析方法層出不窮。鄭紅星[5]和韓宇平[6]等通過建立聯合分布模型采用統計方法計算了南水北調調、受水區水文變量間的豐枯遭遇概率，這種統計方法雖然直觀易懂，但不適用于多維隨機變量遭遇研究，沒有考慮各變量間的相關關系。Copula函數作為一種新興的方法彌補了統計方法的不足，是一種將隨機變量聯合分布與各自邊緣分布相結合的理論聯合分布。目前基于二維及多維Copula函數建立豐枯遭遇聯合分布模型已得到大量實踐應用[710]。此外，傳統風險分析方法只考慮采用降雨、徑流事件的先驗概率計算風險，并沒有考慮后驗知識；貝葉斯網絡作為一種基于貝葉斯條件概率的風險分析方法，既考慮了先驗風險概率，又可以利用后驗信息進行仿真模擬[11]，在水文事件豐枯遭遇風險分析中有其顯著的優勢?？盗岬萚12]運用貝葉斯網絡理論建立了南水北調中線水源區與受水區降水豐枯遭遇風險管理模型，充分利用貝葉斯網絡的情景仿真和后驗推理功能，模擬了不同豐枯組合對調水的影響；Daniel[13]利用并驗證了非參數蒙特卡洛貝葉斯理論在洪水頻率分析中的獨特優勢；H.van de Vyver[14]利用貝葉斯網絡的后驗推理功能對降雨極值強度持續時間頻率相關關系進行了分析，并與傳統方法進行對比驗證了貝葉斯方法的優越性。本文以東江流域上游龍川站、中游河源站及下雨博羅站實測降雨、徑流數據為研究對象，運用Copula函數結合貝葉斯網絡建立流域內豐枯遭遇風險管理模型，為流域內水資源優化配置決策提供理論支持，具有重要的理論意義和實踐意義。

1 數據和方法

1.1 數據來源

本文所用數據均由廣東省氣象局提供，包括東江流域上游龍川站、中游河源站以及下游博羅站三個代表性水文站點1956年-2005年年尺度實測降雨、徑流資料。流域概況及水文站點分布情況見圖1。

1.2 研究方法

1.2.1 二維Copula函數理論

Copula函數是定義在[0，1]區間上均勻分布的多維聯合分布函數，其主要構造形式如下：

1.2.3 多維Copula函數

三維及多維Copula函數的構造形式與二維情況類似，篇幅限制這里不再贅述，其構造形式詳見文獻[17]。對于多維Copula函數的參數估計（以三維為例），不能直接利用參數與變量的Kendall秩相關[CM（22]系數的關系直接計算，一般采用兩階段極大似然進

1.2.4 貝葉斯網絡概述

貝葉斯網絡[18]簡稱BN，是基于貝葉斯定理和條件概率建立的有向無環圖，它由代表變量的節點和連接各節點的有向邊構成，以圖形化的形式直觀地表達系統內各元素之間的相互影響關系。一個完整的貝葉斯網絡模型由網絡結構和網絡參數兩部分組成。圖2所示為一個6節點貝葉斯網絡模型，可用N=〈〈V，E〉，P〉表示[19]，其中：

（1）〈V，E〉表示網絡結構有向無環圖。圖中節點V={V1，V2，…，V6}表示變量，節點間的有向邊E代表變量間的相關關系。對于有向邊（Vi，Vj），Vi稱為Vj的父節點，Vj則為Vi的子節點，沒有父節點的稱為根節點（V1），沒有子節點的稱為葉節點（V6）。規定Vi的父節點集合及非后代節點集合分別用fa（Vi）和A（Vi）表示，則貝葉斯網絡系統包含如下條件假設：

P（Vi|fa（Vi），A（Vi））=P（Vi|fa（Vi））[JY]（6）

即，在給定父節點情況下，子節點與其非父節點條件獨立。

（2）P表示系統根節點概率和非根節點條件概率。由條件獨立性假設可知，非根節點的條件概率分布可用P（Vi|pa（Vi））表示，表達了節點與其父節點的相關關系。給定根節點先驗概率及非根節點條件概率分布，可據此計算包含所有節點的聯合概率分布，圖2所示包含全部節點的聯合概率分布函數為：

2 結果分析

2.1 多情境豐枯遭遇組合概率

流域內降雨、徑流的豐枯變化受地區氣候特性

及下墊面等的影響，不同區間的遭遇概率往往是隨機的。上游出現某一量級枯水年情況時，中、下游可能出現不同量級的豐、枯情況。為定量分析流域內不同區間降雨、徑流的豐枯遭遇情況，計算其遭遇概率及條件概率，文中采用Copula函數，通過建立豐枯遭遇理論聯合分布模型進行研究。頻率分析中我國一般采用PⅢ曲線作為降雨、徑流的邊緣分布，其構造形式如下：

利用線性矩法計算得到流域上、中、下游三個站點降雨、徑流的參數估計結果見表2。分析可知，流域內年降雨量上游龍川站最小為1 61018 mm，中游河源站最大達1 85065 mm；徑流量從上游到下游程遞增趨勢，變異系數分別為04、062和022，說明徑流變化在空間上屬于中等變異。

采用單參數ArchimedeanCopula函數建立降雨、徑流豐枯遭遇的聯合分布函數，不同Copula函數的擬合優度情況與隨機變量的相關性有關[20]?？紤]到流域內降雨、徑流存在較強正相關性，結合幾種Copula函數的構造形式及其參數估計方法，文中選取Clayton Copula函數作為兩站點降雨、徑流豐枯遭遇聯合分布模型的構造函數；三站點豐枯遭遇組合則選取GumbelHougaard Copula函數構造；各站點組合copula聯合分布函數參數估計結果見表3。

2.2 豐枯遭遇條件概率

基于貝葉斯網絡建立豐枯遭遇的風險管理模型，需要確定站點間降雨、徑流豐枯遭遇的條件概率作為網絡的初始參數。以已知上游來水情況，中、下游遭遇條件概率計算為例，公式如下：

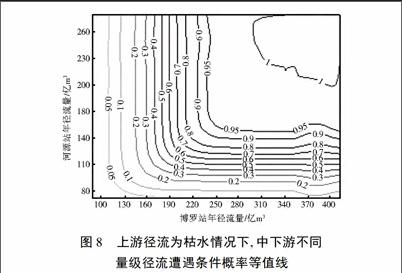
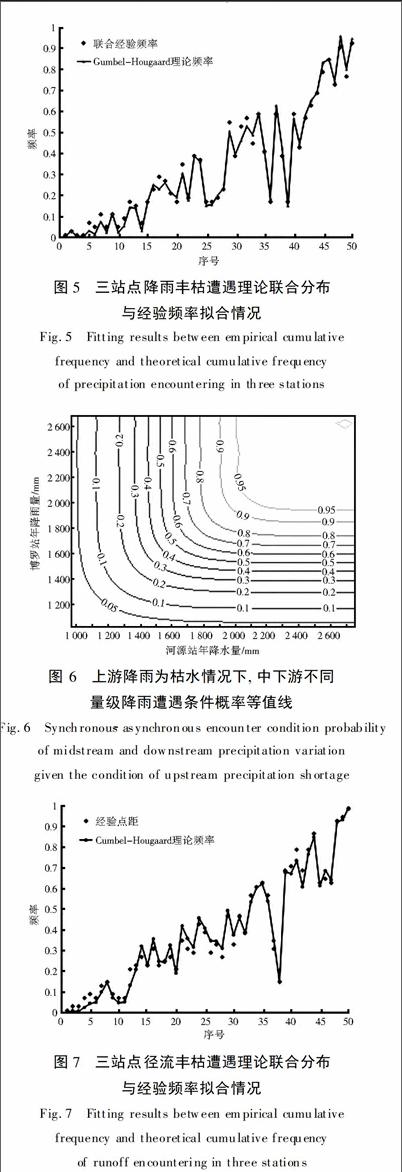
采用GumbelHougaard Copula函數構造三站點降雨、徑流豐枯遭遇理論聯合分布，其與經驗頻率的擬合情況見圖5、圖7，觀察可知，理論分布與經驗頻率擬合情況良好。圖6、圖8所示為上游龍川站降雨、徑流為枯水情況下，中游河源站與下游博羅站不同量級降雨、徑流遭遇的條件概率等值線，可從圖中直接定量出某一固定值豐枯遭遇條件概率大小。如，上游徑流為枯水情況，中、下游同為枯水時的概率P（Y≤y37.5%，Z≤z37.5%|X≤x37.5%）=P（Y≤128.03，Z≤210.66|X≤55.36）=0.685。此外，對比分析圖4和圖8，已知上游徑流為枯水情況，中、下游河源、博羅站不同量級徑流遭遇條件概率等值線有明顯的前移趨勢，等值線密集程度增加，中、下游徑流同豐概率由0260降低到0003，同枯風險概率由原來的0293增加到現在的0685，增長了近25倍，調水不利風險急劇增大。

2.3 流域內豐枯遭遇風險管理模型建立

利用貝葉斯網絡構造流域內豐枯遭遇的風險管理模型一般包括三個步驟：（1）確定網絡結構；（2）確定初始網絡參數；（3）根據后驗知識進行仿真推理。

2.3.1 初始網絡結構確定

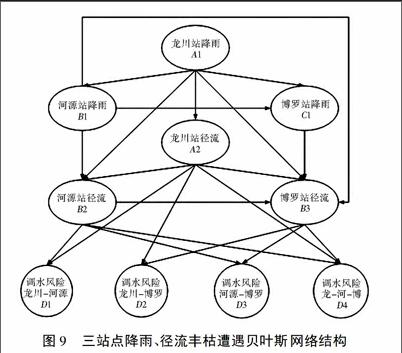
對于網絡結構的確定有兩種方法[22]，一種是利用大量的實測數據通過不同的優化算法進行結構學習，確定最優網絡結構模型，這種方法是在大量數據的基礎上實現的；第二種方法是根據專家知識結合數據間的相關關系，直接勾畫出網絡結構，這種方法對數據的多少要求不高，計算簡便。本文使用第二種方法構造流域內降雨、徑流豐枯遭遇的貝葉斯網絡結構模型，結合流域上、中、下游站點降雨、徑流的豐枯遭遇關系，確定貝葉斯網絡結構模型見圖9。網絡結構圖充分說明了上、中、下游降雨、徑流之間的內在聯系，上游龍川站降雨為根節點A1，其子節點包括河源站降雨B1、博羅站降雨C1以及龍川站徑流A2；葉子節點D1、D2、D3、D4為各站點徑流豐枯遭遇對調水不利的風險概率。

2.3.2 確定網絡參數

貝葉斯網絡結構的參數包括各節點的先驗概率及非根節點的條件概率。根據實測資料計算得各站點降雨、徑流發生豐、平、枯情況的概率，結合Copula函數計算得到各種組合情況的豐枯遭遇概率，輸入到網絡結構中得到貝葉斯網絡初始模型詳見圖10。鑒于東江流域內已建成楓樹壩水庫、新豐江水庫等具有年調節功能的大型水庫，規定，兩個或兩個以上站點同為枯水年是對調水構成風險的情況，其中，三站同枯為調水最不利情況。分析圖10可知，河源站降雨枯水情況發生概率為40%，易于豐水情況發生；博羅站降雨枯水情況發生概率36%，難于豐水情況發生，說明流域內降雨在空間上存在差異性；流域內徑流三站點豐、平、枯水情況發生概率大致相同；龍河徑流遭遇調水不利風險概率27%，龍博、河博徑流遭遇調水不利風險概率均為29%，調水最不利情況（三站同枯）發生概率26%，表明流域內基本可以實現正常調水。

2.3.3 仿真模擬

利用貝葉斯網絡構造流域內降雨、徑流的豐枯遭遇風險管理模型，不僅可以通過實測數據計算各站點豐枯遭遇調水不利情況的發生概率（先驗概率），還可以通過預測某一節點或者某幾個節點的發生情況，作為后驗信息輸入到網絡模型中，利用貝葉斯網絡的反向推理功能，推測出這一節點變化對其他節點條件概率的影響，為決策者制定應急方案提供數據支撐。為充分體現貝葉斯網絡仿真模擬在流域內降雨、徑流豐枯遭遇分析中的優越性，本文以龍川站降雨為枯水和龍川、河源降雨均為枯水兩種情境作為后驗信息輸入到貝葉斯網絡中進行仿真研究。

（1）第一次仿真模擬：將龍川站降雨為枯水情況這一后驗信息輸入到網絡結構中得到仿真計算結果見圖11。對比圖10分析可知，當輸入龍川站降雨為枯水這一后驗信息后，其他節點各種情況的發生概率均發生較大變化。以三站點降雨及調水風險發生概率為例，只輸入先驗知識情況下，河源站降雨豐、枯水情況發生概率分別為34%、40%；博羅站降雨豐、枯水發生概率分別為42%、36%；幾種調水不利情況風險概率均低于30%。輸入龍川站降雨為枯水這一后驗知識后，河源站豐、枯水情況發生概率分別為8%、75%；博羅站發生概率為17%、63%；調水不利風險概率基本在50%以上；各站點枯水情況發生概率有大幅度增加。

（2）第二次仿真模擬：貝葉斯網絡構造風險管理模型對輸入后驗知識的節點個數沒有限制，可能出現同時輸入多節點后驗知識的情況。以輸入兩個節點的后驗知識為例，將龍川、河源站降雨均為枯水這一后驗知識輸入到初始網絡結構中，得到第二次仿真模擬結果見圖12。對比初始網絡模型（圖10）分析可知，輸入龍川、河源站為枯水情況這一后驗知識后，博羅站降雨及三個站點徑流枯水情況的發生概率均有大幅度增加，達到65%以上；博羅站徑流枯水情況發生概率增幅最大，由原來的28%，增加到現在的82%，受上、中游降雨變化影響最為嚴重。就調水風險來看，各站點豐枯遭遇調水不利風險概率均超過55%，其中河源博羅站調水不利情況最易發生，風險概率達67%；三站點同枯風險發生概率63%。針對這一情況，當氣象部門偵測到流域上、中游降雨同為枯水情況時，相關部門需要制定出具有針對性的應急預案措施。

3 結論

針對流域內不同區間降雨、徑流的豐枯遭遇組合狀況，以東江流域上游龍川站、中游河源站及下游博羅站年尺度降雨、徑流為研究對象，運用Copula函數方法建立了流域內不同站點降雨、徑流豐枯遭遇組合的聯合分布模型，結合貝葉斯網絡理論以實測資料及Copula函數計算概率作為先驗知識輸入，構建了流域內三個站點降雨、徑流豐枯遭遇的風險管理模型。通過模型計算，不考慮后驗知識的情況下，各種組合調水不利風險發生概率在25%～30%之間。利用貝葉斯網絡的反向推理功能，分別以上游龍川站降雨為枯水和上游龍川站、中游河源站降雨同為枯水兩種情境作為后驗知識輸入網絡結構，對流域內可能發生的豐枯組合狀態進行仿真模擬計算。計算結果顯示，①輸入上游龍川站為枯水情況時，各站點豐枯遭遇組合調水不利風險概率達到50%左右，其中三站同枯調水最不利風險發生概率達54%；②輸入上游龍川站、中游河源站降雨同枯情況時，站點間降雨、徑流豐枯遭遇調水不利風險概率增加到60%左右，其中河源博羅站調水不利風險概率最大，達67%；文中不同情境下降雨、徑流豐枯遭遇概率和條件概率的計算結果以及基于貝葉斯模型的仿真模擬結果，為流域內水資源的合理調配及可持續利用提供理論支撐，具有理論和實踐意義。

參考文獻（References）：

[1] 冉啟香，張翔.多變量水文聯合分布方法及Copula函數的應用研究[J].水電能源科學，2010，28（9）：811.（RAN Qixiang，ZHANG Xiang.Review on methods of multivariate hydrological joint distribution and Copula function[J].Water Resources and Power，2010，28（9）：811.（in Chinese））

[2] 費永法.多元隨機變量的條件概率計算方法及其在水文中的應用[J].水利學報，1995（8）：6066.（FEI Yongfa.A method for estimating the conditional probability of multirandom variables and its application in hydrology[J].Journal of Hydraulic Engineering，1995（8）：6066.（in Chinese））

[3] Grimaldi S，Serinaldi F.Asymmetric copula in multivariate flood frequency analysis[J].Advances in Water Resources，2006，29（8）：11551167.

[4] 戴昌軍，梁忠民.多維聯合分布計算方法及其在水文中的應用[J].水利學報，2006，37（2）：160165.（DAI Changjun，LIANG Zhongmin.Computation methods of multivariate joint probability distribution and their applications in hydrology[J].Journal of Hydraulic Engineering，2006，37（2）：160165.（in Chinese））

[5] 鄭紅星，劉昌明.南水北調東中兩線不同水文區降水豐枯遭遇性分析[J].地理學報，2000，55（5）：523532.（ZHENG Hongxing，LIU Changming.Analysis on asynchronismsynchronism of regional precipitation in planned SouthtoNorth Water Transfer Areas[J].Acta Geographica Sinica，2000，55（5）：523532.（in Chinese））

[6] 韓宇平，蔣任飛，阮本清.南水北調中線水源區與受水區豐枯遭遇分析[J].華北水利水電學院學報，2007，28（1）：811.（HAN Yuping，JIANG Renfei，RUAN Benqing.Analysis on wetnessdryness encountering of runoff flow between water source region and receiving water region in the Middle Route of the SouthtoNorth Water Transfer Project[J].Journal of North China Institute of Water Conservancy and Hydroelectric Power，2007，28（1）：811.（in Chinese））

[7] 閆寶偉，郭生練，肖義.南水北調中線水源區與受水區降水豐枯遭遇研究[J].水利學報，2007，38（10）：11781185.（YAN Baowei，GUO Shenglian，XIAO Yi.Synchronousasynchronous encounter probability of richpoor precipitation between water source area and water receiving areas in the Middle Route of SouthtoNorth Water Transfer Project[J].Journal of Hydraulic Engineering，2007，38（10）：11781185.（in Chinese））

[8] 馮平，李新.基于Copula函數的非一致性洪水峰量聯合分析[J].水利學報，2013，44（10）：11371147.（FENG Ping，LI Xin.Bivariate frequency analysis of nonstationary flood time series based on Copula methods[J].Journal of Hydraulic Engineering，2013，44（10）：11371147.（in Chinese））

[9] 楊志勇，袁喆，方宏陽，等.基于Copula函數的灤河流域旱澇組合事件概率特征分析[J].水利學報，2013，44（5）：556562.（YANG Zhiyong，YUAN Zhe，FANG Hongyang，et al.Study on the characteristic of multiply events of drought and flood probability in Luanhe River Basin based on Copula[J].Journal of Hydraulic Engineering，2013，44（5）：556562.（in Chinese））

[10] 馮平，牛軍宜，張永，等.南水北調西線工程水源區河流與黃河的豐枯遭遇分析[J].水利學報，2010，41（8）：900907.（FENG Ping，ZHU Yijun，ZHANG Yong，et al.Analysis of wetnessdryness encountering probability among water source rivers and the Yellow River in the Western Route of SouthtoNorth Water Transfer Project[J].Journal of Hydraulic Engineering，2010，41（8）：900907.（in Chinese））

[11] 康玲，何小聰.南水北調中線降水豐枯遭遇風險分析[J].水科學進展，2011，22（1）：4450.（ZHANG Ling，HE Xiaocong.Risk analysis of synchronousasynchronous encounter probability of richpoor precipitation in the Middle Route of Southto North Water[J].Advances in Water Science，2011，22（1）：4450.（in Chinese））

[12] 康玲，何小聰，熊其玲.基于貝葉斯網絡理論的南水北調中線工程水源區與受水區降水豐枯遭遇風險分析[J].水利學報，2010，41（8）：908913.（KANG Ling，HE Xiaocong，XIONG Qiling.Risk analysis for precipitation richpoor encounter between source area and receiving area of the Middle Route of SouthtoNorth Water Transfer Project Based on Bayesnet theory[J].Journal of Hydraulic Engineering，2010，41（8）：908913.（in Chinese））

[13] O′Connell D R H.Nonparametric Bayesian flood frequency estimation[J].Journal of Hydrology，2005，313（s 12）：7996.

[14] H.Van de Vyver.Bayesian estimation of rainfall intensitydurationfrequency relationships[J].Journal of Hydrology，2015：14511463.

[15] 張雨，宋松柏.基于Archimedean Copula的三維干旱特征變量聯合分布研究[J].中國農村水利水電，2011（1）：6568.（ZHANG Yu，SONG Songbai.Research on threedimensional joint distribution of drought characteristics based on Archimedean Copulas[J].China Rural Water and Hydropower，2011（1）：6568.（in Chinese））

[16] 張冬冬，魯帆，嚴登華，等.基于Archimedean Copula函數的洪水多要素聯合概率分布研究[J].中國農村水利水電，2015（1）：6874.（ZHANG Dongdong，LU Fan，YAN Denghua，et al.Research on multidimensional joint distribution of flood characteristics based on Archimedean Copula[J].China Rural Water and Hydropower，2015（1）：6874.（in Chinese））

[17] NELSON R B.An introduction to copulas[M].New York：Springer，2006.

[18] Murphy K P.A brief introduction to graphical models and bayesian networks[J].Borgelt Net，1998.

[19] 周忠寶，馬超群，周經倫，等.基于貝葉斯網絡的多態故障樹分析方法[J].數學的實踐與認識，2008，38（19）：8995.（ZHOU Baozhong，MA Chaoqun，ZHOU Jinglun，et al.Multistate fault tree analysis method based on Bayesian Networks[J].Mathematics in Practice and Theory，2008，38（19）：8995.（in Chinese））

[20] 謝華，羅強，黃介生.基于三維copula函數的多水文區豐枯遭遇分析[J].水科學進展，2012，23（2）：186193.（XIE Hua，LUO Qiang，HUANG Jiesheng.Synchronous asynchronous encounter analysis of multiple hydrologic regions based on 3 D copula function[J].Advances in Water Science，2012，23（2）：186193.（in Chinese））

[21] Singh V P，Zhang L.Bivariate Flood Frequency Analysis Using the Copula Method[J].Journal of Hydrologic Engineering，2006，11（2）：150164.

[22] 張兵利，裴亞輝.貝葉斯網絡模型概述[J].電腦與信息技術，2008，16（5）：4142.（ZHANG Bingli，PEI Yahui.Summary of Bayesian Network[J].Computer and Information Technology，2008，16（5）：4142.