創(chuàng)設教與學動態(tài)探究問題情境，激發(fā)學生的主體性

孫愛萍

摘要：《數(shù)學課程標準》在課程實施建設中明確指出：數(shù)學教學要求緊密聯(lián)系學生的生活實際，從學生的生活經(jīng)驗和已有知識出發(fā)，創(chuàng)設各種情境，為學生提供從事數(shù)學活動的機會，激發(fā)對數(shù)學的興趣以及學好數(shù)學的愿望。本文通過兩則案例剖析，來闡述教與學動態(tài)探究問題情境，從而激發(fā)學生的主體性，達到教學想長。

關鍵詞：問題情境；動態(tài)探究；主體性

課堂上師生互動，始終洋溢著民主、活躍的氣氛，學生因不同的見解而引發(fā)激烈的爭論，在爭論中，學生提出說明和維護各自的觀點，傾聽、理解、支持或反駁別人的意見。能使數(shù)學課堂更加開放和更加具有活力。能充分體現(xiàn)學生的主體作用，教師與學生共同體驗探究過程，共同分享動態(tài)生成的結果，通過共同學習和交互作用，達到教學相長。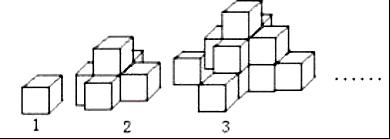

[案例一】學習《視圖》時，通過對疊放的小正方體數(shù)目的探究，培養(yǎng)學生參與意識，歸納探究的能力，體驗成功的喜悅，發(fā)揮學生的主體性。例：如圖，圖1是一個水平擺放的小正方體木塊，圖2、圖3是由這樣的木塊疊放而成的，問題：按照這樣的規(guī)律繼續(xù)疊放下去，至第7個疊放的圖形時，小木塊的總數(shù)是多少？第n個呢？問題提出后，教師叫學生先自行思考，然后回答。

生1：圖1是1個，圖2是（1+5）個，圖3是（1+5+9）個，每一層都比上一層多4個，第n層有（4n-3）個，因此第7個圖有（1+5+9+13+17+21+25）=91 個，第n個圖有[1+5+9+…+（4n-3）]=[1+（4n-3）]n/2=2n2-n（個）

師：回答得很好！還有沒有其它的方法？

生：（小聲討論）

生2：老師，我也有一種方法：第n個圖可以這樣看，前后左右都可以看作（1+2+3+…+n），但應減去中間重復的3次來計算，于是第n個圖有小木塊：

4 （ 1 + 2 + 3 +…+ n ） - 3 n = 4 （ 1 + n ） n/2-3n=2n2-n（個）

師：很精彩！又是一種方法，而且還容易理解。除此之外，還有沒有其它的方法呢？

生3：老師，還有！我悟出了另外一條規(guī)律：

如果把第1圖形有小木塊1個看成 1×1，第2個圖形6個看成2×3，第3個圖形15個看成3×5，第4個圖形有4×7個，…，第7圖形有7×13個，…，依次是一個正整數(shù)乘以一個奇數(shù)，于是第n個圖形就有n（2n-1）=2n2-n（個）

師：真棒！太精彩了！

（此案例還可繼續(xù)引申：如果每個小正方體木塊的邊長為1，一位畫家要給露出的表面涂上顏色，請?zhí)骄客可糠置娣e的變化規(guī)律，此問題力求從不同的角度鍛煉學生的歸納能力。）

這堂課中體現(xiàn)了學生的主體性，激發(fā)了學生的積極性，打開了學生的思維，充分發(fā)揮他們的參與意識，師生思維碰撞，一起體驗成功的喜悅。為深化學生認知結構而設計的認知沖突型情境：以富有挑戰(zhàn)性、探究性且處于學生認知結構的最近發(fā)展區(qū)的問題為素材，引起認知沖突，產(chǎn)生認知推敲，從而激起學生強烈的探究欲望和學習動機。

[案例二】在魯教版《平移》教學中，我創(chuàng)設了這樣一個問題情境，具體教學過程如下：師問：我校一矩形草地中間有一筆直的小路（如圖1），為了達到“曲徑通幽”的效果，現(xiàn)計劃修改為彎曲的小路（如圖2）問題：這兩條小路寬度都為1，哪條小路長？哪條小路面積大？

生1：曲線長。第2條小路面積大，因為曲線比直線長，而它們的寬度都為1，所以第2條小路面積大。

師問：其它同學還有沒有其它的觀點？

生2：我認為兩條小路面積一樣大。

生3：我認為第二條小路面積大。

（很快同學們分成了兩大陣營，說明這個問題引起了同學們的認知沖突）。

師：請幾位同學說一說各自的理由。

生1：長方形的面積等于長乘以寬，眾所周知，曲線比直線長，而它們的寬度相同，所以第2條小路面積大。

師：我覺得他說得很有道理，同學們贊同他的觀點嗎？

下面一片沉默，可以看到不少同學都在苦苦思考這個問題，時間大約有2分鐘。

生4：我認為它們的面積應該相等，我們可以在曲路上作一條垂線，沿這條垂線切割，然后把它們拼起來，就可以構成與路1相同的長方形。所以路1路2面積相等。

生5：我還是認為曲路的面積大，我們可以把曲路拉長，顯然他的長度要比直路的長度長的多，所以曲路的面積大。

生6：我認為兩條路的面積應該相等，如果把曲路拉長，那么它的寬度就會變窄，直路與曲路的面積大小就不好確定，而用切割的辦法可以準確的算出曲路的面積，這種做法是可行的。

生7：如果草坪可以移動，我們可以將左、右兩邊的草坪拼合在一起，那么剩下的部分就是曲路的面積。

可以看到這個情境的創(chuàng)設確實引起了學生的認知沖突，學生在兩種結論間徘徊，最后在同學的相互交流、相互啟發(fā)下得到了結論。

教與學動態(tài)探究問題情境的創(chuàng)設要注意要注意以下幾點：

一、尊重學生的已有經(jīng)驗

新課標指出：數(shù)學教學活動必須建立在學生的認知發(fā)展水平和已有的知識經(jīng)驗的基礎之上。生活中積累的經(jīng)驗，運用已有知識過程中獲得的經(jīng)驗以及從已有數(shù)學思想方法中獲得的經(jīng)驗，能幫助學生發(fā)現(xiàn)問題，提出問題，當呈現(xiàn)給學生一個熟悉的學習材料時，很快就會激活學生原有的經(jīng)驗儲存，學生在產(chǎn)生“跳一跳能摘到桃子”的第一感覺后，馬上就會與同伴交流看法，以飽滿的熱情投入到研究中去。

二、找準“探究點

找準“探究點”是實現(xiàn)教與學動態(tài)探究的關鍵。所謂“探究點”是學生為解決問題而進行的能與原有知識和經(jīng)驗建立起有效聯(lián)系的學習活動。在設計這一活動內(nèi)容時，就要考慮適不適合以探究的方式學習。并非所有的內(nèi)容都適合探究式學習，大量的課例研究表明，“探究點”確立的恰當與否成為決定一節(jié)課成敗的重要因素。

三、看準引導時機

教師對學生的引導不是隨機的、經(jīng)常的，否則會干擾學生思維。只有在需要或認為有必要時引導：

1、當學生的探究活動偏離目標時，教師應及時引導。

2、當學生因思維定勢等原因產(chǎn)生思維障礙或思維困難，無力自拔或克服時。

3、當學生思維出現(xiàn)閃光點，但又稍縱即逝時。

四、把握引導力度

教師的引導應是自然的、策略的。既要避免空洞乏力，使學生不得要領，無所適從的所謂“引導”，也要避免過于直截了當，甚至包辦代替，把引導變?yōu)椤爸甘尽钡臓恳＝處煹囊龑獋戎卦谔骄康姆较颍椒ê筒呗陨稀７彩菍W生經(jīng)過努力可以完成的事情，教師應盡力創(chuàng)造條件讓學生獨立或以合作的方式去完成。

總之，教與學動態(tài)探究問題情境的創(chuàng)設要貼近學生的最近發(fā)展區(qū)，使學生產(chǎn)生認知矛盾，引起思維困惑，激起疑問形成。激疑為先，討論在后，點撥思路在最后，激疑一定不要忙著解惑，能啟迪學生的思維，激發(fā)學生深入探究的情感，這是教與學動態(tài)探究問題情境創(chuàng)設的關鍵，從而才能激發(fā)學生的主體性，達到教學想長。

參考文獻

[1] 張奠宙.趙小平.當心“去數(shù)學化” .《數(shù)學教學》，2005.6.

[2] 王志民.透析問題情景中的問題.《基礎教育課程》，2006.9.

[3] 張向榮.數(shù)學有效課堂教學情境創(chuàng)設策略的研究.《現(xiàn)代婦女（下旬）》 ，2014.02.