例談高中數(shù)學中的定點問題研究

例談高中數(shù)學中的定點問題研究

☉江蘇省寶應縣安宜高級中學 鮮黎

“定點”問題是解析幾何試題中常見的一類題型，在近幾年的高考或模擬試題中頻繁出現(xiàn)，因為這類題型不僅體現(xiàn)了數(shù)學文化美，而且體現(xiàn)了哲學中動與靜的辯證統(tǒng)一的關系，所以備受命題專家的青睞.下面筆者結合平時的教學實踐，談談對這類定點問題的研究.

一、直線與圓的一類定點問題探究

高中數(shù)學直線方程和圓方程中有一類涉及定點和定值的問題.這類問題中一般都有變量或動點，但最終的數(shù)值或點卻是一定的.解決這類問題，一般都用方程思想探得定值或定點，利用等式恒等的性質，可求出定點、定值.

例1如圖1，已知圓M：x2+（y-2）2=1，Q是x軸上的動點，QA，QB分別切圓M于A，B兩點.求證：直線AB恒過定點.

證法1：如圖1，設A（x1，y1），B（x2，y2），Q（x0，0），

圖1

x1x+（y1-2）y-2y1+3=0.同理x2x+（y2-2）y-2y2+3=0.

把Q（x0，0）代入上面兩式得到x1x0-2y1+3=0，x2x0-2y2+ 3=0，

所以A（x1，y1），B（x2，y2）同時滿足直線方程xx0-2y+ 3=0，即直線AB方程為xx0-2y+3=0，由x0的任意性得到定

證法2：設Q（x0，0），以MQ為直徑的圓（x-0）（x-x0）+（y-2）（y-0）=0，即x2+y2-x0x-2y=0.圓M：x2+（y-2）2=1，即x2+y2-4y+3=0，兩圓相減得到公共弦所在的直線方程x0x-2y+3=0，由的任意性得到定點（0，）.

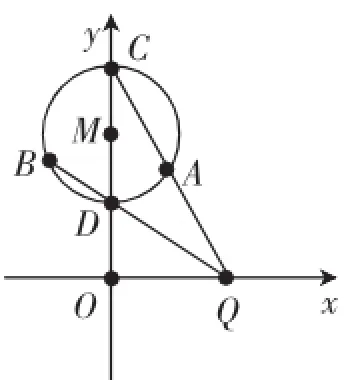
圖2

證法3：直線AB也可以看成是以Q為圓心，MA或QB為半徑的圓，和圓M的公共弦，證法如證法2.

變題1如例1中的圓M交y軸從上而下于C，D，如圖2，連接QC，QD交圓M于A，B，證明：直線AB經(jīng)過定點.

證明：設Q（x0，0），C（0，3），D（0，1）.

又因為Q關于原點的對稱性，這個定點一定在y軸上，令x=0，得到

變題2若把圓M改為x2+（y-2）2=r2（0＜r＜2）.

（1）例1的定點又是什么？有什么發(fā)現(xiàn)？

（2）若把圓M改為x2+（y-b）2=r（20＜r＜b）呢？

11111

把Q（x0，0）代入上面直線方程得到x0x1-2y1-r2+4=0.

同理可以得到x0x2-2y2-r2+4=0.

所以A（x1，y1），B（x2，y）2同時滿足直線方程x0x-2yr2+4=0.

由x0的任意性知

11111

把Q（x0，0）代入得到x0x1-by1-r2+b2=0.

同理可以得到x0x2-by2-r2+b2=0.

所以A（x1，y1），B（x2，y2）同時滿足直線方程x0x-byr2+b2=0.

由x0的任意性知，

二、拋物線定點問題

當拋物線的弦所在直線過定點時，拋物線對稱軸上一點與弦的兩個端點形成的直線斜率或夾角平分有一定的定點性質，另外，在拋物線中還有其他幾條定點問題，現(xiàn)例舉說明幾條結論.

結論1拋物線C：y2=2px與直線y=k（x-m）交于A，B兩點，O是坐標原點，則k·k=-

OAOB

證明：設A（x1，y1），B（x2，y2），則

逆命題1拋物線C：y2=2px上兩動點A，B，O為坐標原點，若·k=-，則直線AB過定點（m，0）.OB

結論2拋物線C：y2=2px與直線y=k（x-m）（其中m＞0）交于A，B兩點，已知點E（-m，0），則∠AEB的平分線是x軸.

圖3

12120，代入（*）得直線AE，BE的傾斜角互補，結合圖3知，∠AEB的平分線是x軸.

逆命題2已知點E（-m，0）（其中m＞0），拋物線C：y2=2px上兩動點A，B，若∠AEB的平分線是x軸，則直線AB過定點（m，0）.

結論3拋物線C：y2=2px與直線y=k（x-m）（其中m＜0）交于A，B兩點，已知點E（-m，0），則∠AEB的平分線平行于y軸.

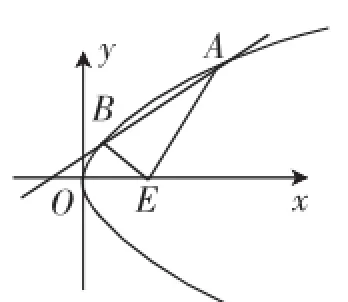
圖4

12120，代入（*）得直線AE，BE的傾斜角互補，結合圖4知，∠AEB的平分線平行于y軸.

逆命題3已知點E（m，0）（其中m＞0），拋物線C：y2= 2px上兩動點A，B，若∠AEB的平分線平行于y軸，則直線直線AB過定點（-m，0）.

三、圓錐曲線中的定點問題

圓錐曲線中的定點問題是近幾年高考中的熱點，題型變化多端，靈活新穎.現(xiàn)舉例說明圓錐曲線中定點問題的解題策略.

（1）求雙曲線C的方程；

（2）過雙曲線C的右焦點F作直線與雙曲線左，右兩支分別交于點A，B，點B在直線x＝上的射影是D，求證：直線AD過定點.

圖5

解：（1）雙曲線方程為x2-＝1（過程略）.

（3-k2）x2+4k2x-（4k2+3）＝0，Δ＝36（k2+1）＞0恒成立.

設A（x1，y1），B（x2，y2），則D

x1x2＝①設直線AD與x軸交于點M（t，0），只要證明t為常數(shù)即可.

證法1其思路很自然.亮點在于，根據(jù)雙曲線C關于x軸對稱，預設定點在x軸上，即D（t，0）.先將t表示為x1，y1，x2，y2的關系式；再消y1，y2轉化為關于x1，x2的關系式；最后再消x1，x2轉化為關于k的關系式，化簡得結果，體現(xiàn)了化歸與轉化的思想.避免了復雜思路：將AD的方程設為y-變形得形如方程y-y0＝f（k）（x-x0），從而直線AD過定點（x0，y0）.

證法2，體現(xiàn)了整體消參的思想，計算過程明顯簡單.

下推廣：

類比雙曲線，可得橢圓與拋物線相關結論：

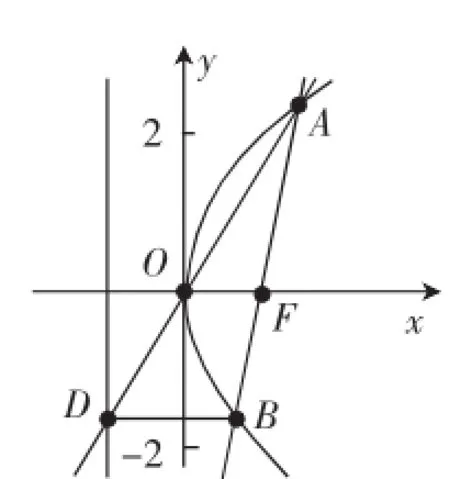
圖6

結論3如圖6，過拋物線焦點F的直線交拋物線于A，B兩點，點B在拋物線準線上的射影為D，則直線AD必過拋物線頂點（定點）.（證明略）

幾種圓錐曲線概念具有共生性，性質也有統(tǒng)一性，通過舉一反三還可發(fā)現(xiàn)更多結論，如以上變式等.