高中數學教學“最近發展區”的確立策略與實踐

賀石楚

[摘 要] 最近發展區理論要求教師在教學中不僅要關注到學生現有的水平發展，學生可能達到的水平發展也同樣是應該注重的. 因此，教師應立足于學生長遠的發展并為他們架起從原有認知水平到潛在認知水平平穩對接的橋梁，使得學生在原有認知水平基礎上進行對接，向更高的發展層面攀登.

[關鍵詞] 最近發展；高中數學；學生

蘇聯教育家維果茨基所提出的最近發展區理論將學生發展的水平分為現有發展水平和即將達到的發展水平兩種. 這兩種發展水平之間的差異便是我們經常提及的“最近發展區”. 它一般表現為個體獨立完成與憑借他人幫助完成之間的水平差異，相對來說這是最為敏感且易于接受教學影響的階段，因此，高中數學教學應該著眼于最可能影響學生水平發展的“最近發展區”以達成學生最為有效的知識學習與能力發展. 如何確立最近發展區呢？本文就該話題談幾點筆者的思考.

根據初高中學生思維特征確立“最近發展區”

對初高中這樣年齡階段的學生進行思維發展方面的觀察與分析，我們不難發現初中學生的思維發展主要還是以形象思維為主，并在此基礎上正逐步向經驗型的抽象思維過渡.但大多數高中學生的經驗型抽象思維已經趨向于成熟，并在此基礎上逐步向理論型抽象思維過渡，甚至有的學生已經達到辯證思維的初級階段. 當然，剛剛跨入高中大門的學生中還是有相當一部分是不能適應這種思維要求的變化的，俗稱的思維定式就往往在這部分學生身上尤為體現，這部分學生也正因為這樣的思維定式才會覺得高中數學學習特別有難度. 因此，初高中學生思維平穩對接的“突破口”是教師在日常教學中尤其應該關注并積極探究的，教師應對高一新生的思維特征以及高中數學學科的特征展開分析和探究，使得學生數學學習思維跳躍的最近發展區能夠被精準地定位，然后根據這個定位進行教學程序的有效制定，將自己的教學盡量設計成最符合學生思維結構水平的活動，并使教學活動兼具強度與難度，把“跳一跳就能夠著的桃子”擺在學生面前，以此來觸動學生思維的積極性與可拓展空間. 以二次函數為例，高中新課程在此知識點的要求上高了很多，教師可以在學生初中所學知識的基礎上對該知識點進行鞏固與適度的加深和拓寬，將具體問題呈現在學生面前，使學生能夠借助具體問題的解決來掌握二次方程根的區間分布等相關知識.

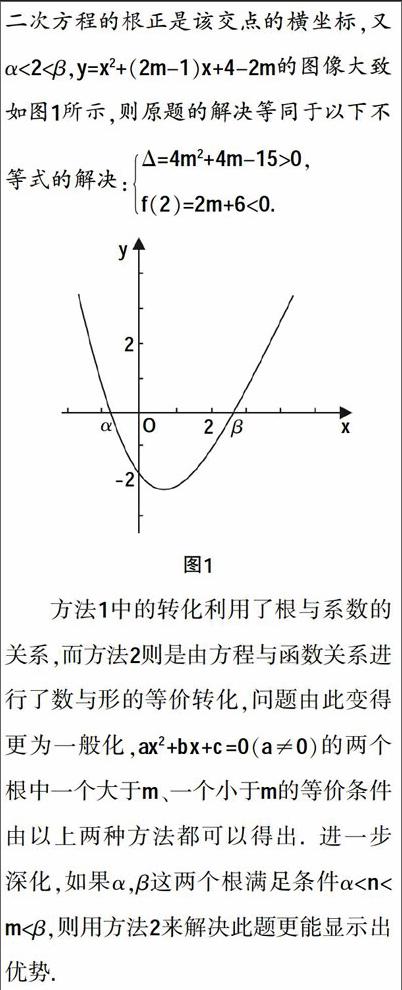
例：若α，β是方程x2+（2m-1）x+4-2m=0的兩個根，且α<2<β，求m的范圍.

方法1：由二次方程根與系數關系可得α+β=1-2m，αβ=4-2m，由α<2<β得α-2<0且β-2>0.

根據題意，原題可以轉化為

Δ>0，（α-2）（β-2）<0，

即Δ=4m2+4m-15>0，αβ-2（α+β）+4=2m+6<0.

方法2：相應二次函數與x軸有一交點，二次方程的根正是該交點的橫坐標，又α<2<β，y=x2+（2m-1）x+4-2m的圖像大致如圖1所示，則原題的解決等同于以下不等式的解決：Δ=4m2+4m-15>0，f（2）=2m+6<0.

方法1中的轉化利用了根與系數的關系，而方法2則是由方程與函數關系進行了數與形的等價轉化，問題由此變得更為一般化，ax2+bx+c=0（a≠0）的兩個根中一個大于m、一個小于m的等價條件由以上兩種方法都可以得出. 進一步深化，如果α，β這兩個根滿足條件α

從這個例題中我們不難看出變式訓練對學生思維訓練的積極意義，學生思維方法的改變、思維能力的提高與發展、思維品質的形成都在針對性的變式訓練中得到了有意義的鍛煉和發展，學生數學思維的各方面因素都向著更高水平層次邁進了一大步.

找準學習方法轉換的基點確立“最近發展區”

愛因斯坦有個廣為人知的成功公式：A=X+Y+Z，這個公式里的A，X，Y，Z分別代表了成功、艱苦勞動、正確方法以及少說廢話這幾個意思. 這個著名的成功公式也向人們表達了成功的三大要素究竟是什么. 學習中也有類似的成功公式，我們總結下來可以這樣表示：學習成功=心理素質+學習方法+智能素質. 其中科學學習方法的掌握是學好高中數學最為重要的條件. 初中階段的數學學習一般只要將概念、公式以及例題類型進行一定的記憶就不會有太大問題，獨立思考與歸納總結相對來說并不是特別需要的. 高中數學的學習對學生的思考、歸納總結、應用、思想方法的掌握等都提出了比較具體的要求，學生的自主學習與研究性學習是高中數學學習中必不可少的. 一般來講，初中數學學習的方法用到高中數學學習中往往是不夠的，學生如果還是局限于初中數學方法的運用，高中數學就會給他造成極大的障礙. 因此，教師一定要整理、分析、歸納出初高中數學學習方法的異同，并貼近學生最近發展區進行數學學習的優化訓練，使得學生盡早養成良好的學習方法與習慣. 制定學習計劃、課前自學、及時復習、解決疑難、系統小結以及課外學習都是高中數學學習中應該養成的良好學習方法與習慣的各個組成因素.

找準學習心理的“落差”點確立“最近發展區”

很多剛剛跨入高中大門的學生都對自己的數學學習信心滿滿，但是隨著一段時間的學習之后，很多學生會發現自己數學學習的實際情況往往與自身的期望值相差甚遠，心理落差也就自然形成了. 高中數學學習其實是所有學科中可能產生這種現象最為明顯的學科，甚至一些中考尖子生也會出現大幅度的數學成績滑坡現象，很多學生在數學學習中投入大量的時間與精力但仍然沒有很好的效果，覺得高中數學難度太大的想法自然就產生了. 高中數學學習的信心一步一步慢慢褪去，自卑心理一步一步慢慢蒸騰，學習被動、意志薄弱的現象在高中數學學習中比比皆是，高中數學學習能力的發展遭受了極大的遏制. 因此，學生原有的期望值與實際學習情況之間的落差心理也是教師日常教學中應該關注的，這樣對于學生心理對接的最近發展區才會有更精準的定位，高中數學學習心理平穩對接才會更加成功.

1. 明確差異，引起重視

教師在高一開學之初就應該將初高中數學學習內容的差異、學習方法的差異、課程要求的差異、思維的差異對學生進行明確，使學生對初高中數學學習產生不同的認知，將自己高中數學學習的心理預期擺正，從而減輕自身高中數學學習的壓力.

2. 正確認知，調節自我

教師面對一部分已經產生心理落差的學生應積極疏導，幫助他們客觀分析自己的情況并重新找準自己在數學學習上的位置，及時修正自己的學習計劃與目標并腳踏實地地付諸行動.

3. 及時激勵，增強自信

教師對待有心理落差的學生還應為其創造合適的鍛煉機會，幫助學生在基礎性的鍛煉中重拾信心. 比如，在一些簡答問題的回答、簡答例題的解答中及時給予肯定與鼓勵.

數學難學可能是高中學生與家長普遍的內心獨白，事實上，高中數學與初中數學相比確實存在著很大的“跨度”，這些思維方式、學習方式上出現的“跨度”甚至在學生的數學學習中造成了學習的“斷層”現象，合理地確立最近發展區，能夠助推學生有效地學習知識，提升能力，在學習的過程中增強學習的自信心.