數形結合的幾種方式

周愛華??

摘要：數形結合作為數學研究的主要對象，能夠使復雜問題簡單化、抽象問題具體化，是優化解題途徑的主要方法之一。本文結合多年實踐教學經驗，主要探討了數形結合思維在概念教學、計算教學、公式推導和課堂練習中的應用，希望通過多角度的說明，加深學生對該方法的理解。

關鍵詞：數形結合；教學；應用

我國著名數學家華羅庚先生曾說：“數與形，本是相倚依，焉能分作兩邊飛。數無形時少直覺，形少數時難入微。數形結合百般好，隔離分家萬事非；切莫忘，幾何代數統一體，永遠聯系，切莫分離！”這句話中華羅庚先生正確地說明了“數”和“形”之間的相互依賴、相互制約，是種辯證關系，對數形結合思想最通俗的、最深刻的剖析。《課標》明確指出：“數學學習，學生能獲得適應社會生活和進一步發展所必需的數學的基礎知識、基本技能、基本思想、基本活動經驗。”由此可見數學思想是數學的靈魂和精髓，是數學素養的本質所在。利用“數形結合”的思想方法能使數和形在學習中有機地統一起來，借助于形的直觀來理解抽象的數，運用數來細致入微地刻畫形的特征，把抽象內容形象化，對于學生理解數學實質有很大的幫助，并且從一定意義上使教學更加快捷與高效。

一、 理論知識夾雜數形結合

概念是小學數學知識重要組成部分且多是理論性語言，因此學生理解起來有一定難度。使用清晰的圖形可以讓不具體的理論課堂更加明了，學生們很容易就懂得一節課的重點，輕松理解概念。

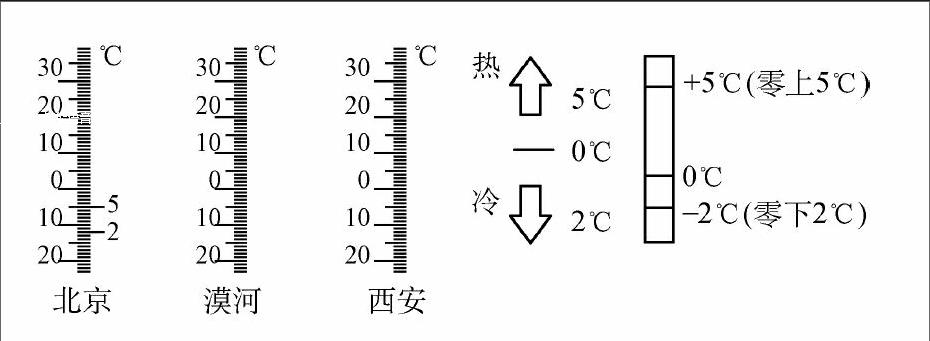
四年級一書《生活中的負數》這一節中，用正負數表示生活中具有相反意義的量是本節課的教學重點，體會負數的意義及0的內涵是難點。如果直接把這個概念灌輸給學生，再做大量的習題來鞏固和提高學生的運用能力，效果可想而知是不好的。

在教學過程中，從學生熟悉的溫度引入，通過觀察溫度計進行教學，利用數形結合幫助學生建立一個形象的數學模型，從而加深了學生對負數的理解。

二、 計算教學中滲透數形結合

學生算數學題目時要結合數形結合，老師要教學生們正確理解學生題目，計算題目的方法就是算理，在課堂上老師上課時，老師要用正確的方式教導學生理解題目，學生在理解題目的基礎上對算法有一定的了解，就相當于這句俗語“知其然，知其所以然。”例如數形結合。

像分數這一節課中：把一張紙的4/7平均分成3份，每份是多少？學生很難理解算理，算出式子4/7÷3以后，可以讓學生用圖形來表示出4/7÷3這個算式。

每份中47的13，就是這張紙的421。

47÷3=47×13=421

先把這張紙平均分成7份，取其中4份，再把4份平均分成3份，取其中1份。

47÷3=421

然后，對學生進行分組，讓學生跟自己的組員交流，分別拿出自己的圖形，看看優缺點，修改自己的圖形，讓學生更好理解圖形的意思。

最后，可以全班一起進行交流，全面理解數形結合，不管是看到式子還是圖形都可以想到另外一方，學生自覺的建立數形結合的這個概念，也會更加清楚的利用。

三、 公式推導中滲透數形結合

進行公式推導的過程也是學生學習數形結合的重要環節，公式推導會讓學生產生死記硬背的想法，達不到讓學生自己思考進行解題的思路，數形結合的方法可以讓學生避免死記硬背，產生自己的思路、條理，解題也會有很多種不同方法。幫助學生建構數學思想方法，從而能很好提高學生聯系實際，靈活解決數學問題的能力。

解題過程中，解題的步驟通常是：老師在講臺利用ppt的形式逐一演示面積公式的推導過程，其中夾雜一兩個案例，隨后讓學生在課堂上利用公式解決不同類型的數學題目。可是學生經常把圓柱側面積和體積這兩個公式弄混了，為什么呢？因為很多學生的解題活動完全建立在簡單記憶和機械模仿上，沒有真正理解為什么是2πrh和πr2h，

如果讓學生動手剪一剪圓柱體，把側面展開，再結合示意圖，學生才能真正理解沿高剪開后圓柱的側面展開是一個長方形，長方形的長就相當于圓柱底面周長，寬相當于圓柱的高，所以圓柱的側面積是長×寬也就是底面周長×高。

長方形面積=長×寬

=底面周長×高

=2πr×h

=2πrh

四、 課堂練習中滲透數形結合

在學生們解決一些困難的題目時，并且數字很復雜，就可以利用數形結合的方式對題目進行簡單的分析，讓很復雜的關系變得很清晰。

例如：食品支出占家庭總支出的55%，其他支出占家庭總支出的45%，食品支出比其他支出多620元，家庭總支出是多少元？

先把題中的數量關系譯成圖形，再從圖形的觀察分析可譯成：在本題中，關鍵是要把總支出看作單位“1”，從而推知多出的620元，所對應的百分率是10%。

解：設總支出為x元，那么食品支出是55%x元，其他支出是45%x元。

55%x-45%x=620

620÷（55%-45%）=620÷10%=620÷0.1=6200（元）

這樣不管是算術解還是方程解，學生都容易理解。

從這道題目中可以很清晰地看出：“數”和“形”不僅是讓學生們利用簡單的方式解決困難的題目，它還可以讓學生們的思維更加開闊，解題方法也會文思泉涌，解題過程中，隨著題目答案的解出，學生的思維也在增長，數和形是相互支持，共同發展的，二者結合讓解題更加簡單。

綜上，形是數的直觀呈現，數是形的邏輯表達，數與形是辯證統一的。數形結合，能把學生的形象思維與邏輯思維有機地結合起來，做到數中有形，形中有數，培養學生的良好的數學素養。