對初中數學課堂教學有效提問的思考

王東

[摘? 要] 當前的初中數學教學提問中仍然存在著急于求成、不求質量、設計隨性的諸多問題，教師在實際教學中應圍繞學生與知識設計出更多導向性、建設性或具有懸念的問題，適當把握問題的數量與質量并令學生在充裕的思考中獲得思維的發展與知識的掌握.

[關鍵詞] 初中數學;有效提問;存在問題;提問技巧

學生在課堂學習中往往因為教師的有效提問而產生更多的思考與優質思維，學生在活躍的思維碰撞與分析討論中也會因為教師的有效提問而更易得出問題的答案. 教師圍繞教學內容與目標并根據邏輯結構而設計的有效提問能夠滿足學生思維發展的需要，學生主體地位得到彰顯的同時也令自己的學習變得更加主動，使學習興趣得到有力激發并對課堂學習投入更多的精力與思考. 學生自主學習與探究的意識、能力得到培養的同時也使其更易產生自己的理解與觀點.

當前初中數學課堂提問存在的問題

1. 急于求成

相當一部分教師往往太過重視學生的考試成績而在課堂教學中表現得更加功利. 這部分教師在平時的教學中傾向于大量“刷題”以期學生數學成績的提升，課堂教學提問的環節是有的，但往往不能給予學生充裕的時間思考. 很多學生在教師的匆匆提問與回答之間無法對問題進行深入思考，一些數學能力不甚優秀的學生給出的答案若是不夠準確，教師也常常忽略他們的思考而傾向于答案的直接給出. 學生在沒有引導、追問、辨析的思考過程中牽強附會地接受答案，學生的個性思維被抑制于教師的預設與輕視中，無法真正獲得思維的鍛煉與發展.

2. 不求質量

數學課堂教學中的提問是所有教師經常運用的手段，但有些教師在課堂教學中對提問的頻繁使用常常令學生應接不暇，學生思考淺薄或不加消化的狀態令其思維發展受到嚴重的鉗制. 大量不求質量的提問使課堂教學看上去熱鬧非凡，但學生的思考卻往往停留于問題的表層而無法得到實質上的發展.

3. 設計隨性

一些教師在課堂教學中往往對問題不能進行深入思考，并表現出設計上的隨性，以肯定或否定答案呈現的問題在課堂教學中比比皆是. 學生在眾多判斷類的問題中根本無需深入思考，數學能力優秀的學生一般能清晰地做出反應，但能力不足的學生就會跟風或猜測問題的答案，這些無法促進學生深入思考并脫離學生“最近發展區”的問題往往使提問效果大打折扣.

初中數學課堂提問的技巧

1. 設計懸疑問題，激發興趣

教師在具體的教學中應對教學內容進行剖析并尋找其切入點，設計出與生活實際緊密關聯的問題以引發學生對新知識的好奇，活躍學生思維的同時將其探索問題的興趣有力誘發并營造出活躍的課堂氛圍. 不僅如此，教師在具體教學中還可以變換不同的角度進行懸疑問題的設計，使學生能夠在興致盎然的探索中不斷領悟數學的魅力.

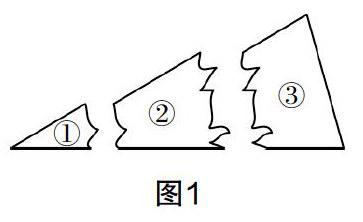
例如，教師在“三角形全等”這一內容的教學中可以這樣提問：圖1是華華在鄰居家不小心打碎的一塊玻璃，他準備去店里重新配一塊作為賠償，懶惰的華華去配玻璃時只帶了①②③中的一塊，大家覺得他應該帶哪一塊去才能配出與原來一樣的玻璃呢？

學生紛紛感覺此問題比較有意思并舉手回答：

生1：帶①去，塊頭小，好攜帶.

生2：帶②去，比較利于補全原來玻璃的樣子.

生3：……

師：大家的猜想中到底哪個才是對的呢？我們不妨先來學習今天的主要內容——三角形的全等，學習完這一內容之后我們再來驗證哪個猜想是正確的.

教師在此處設計的貼近生活又緊緊圍繞教學內容的問題為學生創設出了廣闊的猜想思維空間，學生在思索中也真切感受到了新知識在生活中的重要價值與運用，學生對新知識的學習與探索也因此展現出濃厚的興趣. 這種與生活實際融合的懸疑問題不僅將數學的生活應用價值展現無余，學生的學習主動性與探索熱情也會變得空前高漲.

2. 拆解核心問題，激發探索

教師在實際教學中設計出一些具有導向性的問題并將知識的重難點蘊含其中，能夠引導學生在積極思考中對重難點進行探觸與思索并逐步獲得正確而深刻的理解. 教師在難度較大的應用題教學中可以將問題進行分解并設計出一系列的導向性問題以幫助學生進行逐層思考.

例如，某商店銷售節能燈、白熾燈這兩種照明效果與使用壽命一樣的燈泡，已知節能燈與白熾燈的瓦數分別為0.011千瓦、0.06千瓦，售價分別為60元、3元，兩者相比，節能燈更加省電但價格較高，假如電費為0.6元/千瓦，選用哪種燈更加經濟呢？

很多學生在面對這樣一道語言表述較多的應用題時紛紛感覺太難理解以致無法下手，事實上，教師在此題的教學中可以設計出以下向導性問題以幫助學生解題：

（1）題中所表達的核心問題是什么？

（2）費用應怎樣計算？

（3）假如將照明時間假設成t，表達式應怎樣列出？

（4）兩種燈費用一樣時的照明時間為多少小時？

圍繞核心問題拆解成的若干問題使學生對此題進行了逐層深入的思考并獲得了最終的順利解題.

3. 設計建設性問題，拓展思路

教師根據教學內容與學生思維發展設計出合理的建設性問題能夠有效培養學生探究性學習的習慣，為學生創造出創新空間的同時也對其思考的獨立性養成起到很好的作用. 學生在這些開放性問題的思考與回答中能夠更好地表達出自身獨有的見解，思維發散的同時也令課堂氛圍更加活躍而熱烈.

例如，教師在“多邊形內角和”的教學中可以設計如下問題：一個五邊形瓷磚被截掉一個角之后還剩幾個角呢？新的圖形的內角和應該是多少度？學生在分組討論之后紛紛回答：

生1：應該剩下四個角，其內角和應該為360°.

生2：剩下六個角，其內角和應該為（6-2）×180°=720°.

生3：仍然是五個角，其內角和應該為（5-2）×180°=540°.

學生在這一問題中既有實踐型的操作與探索，又有發散型的思考與拓展. 這一開放性的問題不僅能令課堂氛圍更加熱烈，還能使學生對五邊形去掉一個角后發生的變化進行探索. 學生在不同情況的探索以及最后的交流中不僅能感受到數學的無窮魅力，探究學習的意識與能力也得到了有意義的鍛煉與發展.

4. 預留充足的思考空間

信息從傳遞到存儲經歷的時間大約為1秒鐘，這是心理學研究得到的數據. 教師在問題提出以后若是不能給予學生足夠的思考空間，學生的思維根本無法得到應有的觸動與深入發展，因此，教師在具體教學中一定要為學生預留足夠的思考空間并促成學生自我的充分展現.

5. 適度提問

教師在同一教材上所設計的不同提問往往會收到不一樣的效果，這正是由于教師對教材內容的理解與問題把握上的不同. 很多初中數學教師在具體的課堂教學中并不特別擅長提問，有的問題特別簡單以至于學生不用思考，有的問題難度太大以至于學生百思不得其解，有的問題量太大以至于學生疲于應付，有的問題量太小以至于課堂氛圍死氣沉沉.

例如，我校每月的數學公開課活動中，一位年輕教師在課堂上提出的問題竟然有四十個之多，學生思維漫天飛舞的同時也將其教學節奏嚴重打亂，很多“是不是”“對不對”“好不好”的提問令學生忙于回答“是”或“不是”等，這種簡單的提問方式使學生忙于應付而無法令其深入問題的本質，課堂看似熱鬧非凡但實質上卻并未對學生的思維發展起到很好的作用.

對數學課堂有效提問的思索，使筆者的數學課堂教學充滿了變化，有了一種活力，極大地促進了筆者的數學課堂教學效益，提高了學生的數學能力和水平. 總之，教師在具體的教學中一定要把握知識的本質與重難點，依此設計出難度與數量都比較合理的問題以幫助學生深層思考，使學生的身心被牢牢牽引的同時對知識形成生動而富有活力建構.