看清線性規劃的“真面目”

☉江蘇省常州市北郊高級中學 包靜怡

在高三數學復習中，學生對于線性規劃掌握的程度往往不盡如人意.究其原因，很多學生對于線性規劃的認知僅僅停留在一個非常表象的層面，即看到題目中出現線性約束條件（二元一次不等式組），才會想到用線性規劃來解題.如果題目條件中沒有出現約束條件，或者給出的約束條件形式不夠常規，又或者換成了函數、數列等其他的背景，學生在解題中都容易出現問題.

下面我們通過對幾個典例的研究，從而看清線性規劃的“真面目”.

一、題目中有約束條件，但是背景融入了其他數學知識

例1設f（x）=ax2+bx，且1≤f（-1）≤2，2≤f（1）≤4，則f（-2）的取值范圍為_______.

例2 等差數列｛an｝中，已知首項a1及公差d都是整數，前n項和為Sn.若a1≥6，a11＞0，S14≤77，求數列｛an｝的通項公式.

解析：由題意可得到關于a1，d的不等式組N*，則d=-1.代入不等式組得到10＜a1≤12，a1∈N*，則a1=11或12.所以an=12-n或an=13-n.

通過這兩個例題，我們發現其實不在于題目給出的背景是什么數學知識，只要可以從中抽離出約束條件及目標函數，就可以轉化為線性規劃解決.

二、題目中沒有約束條件，需要尋求約束條件

例3若函數（fx）=x2+ax+2b在區間（0，1）和（1，2）內各有一個零點，則的取值范圍是_________

解析：若函數f（x）=x2+ax+2b在區間（0，1），（1，2）內組對應的平面區域，如圖1，因為，則z的幾何意義為區域內的點到點D（1，2）的斜率，根據線性規劃知識可得范圍為

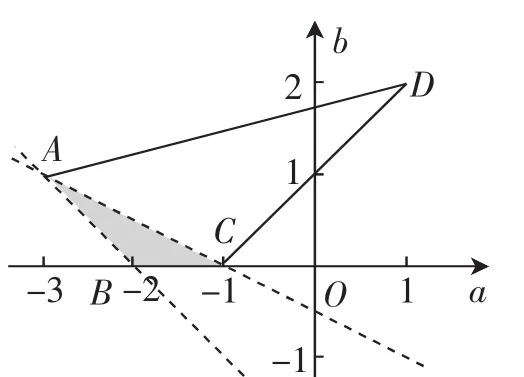
圖1

本題給出的條件是二次函數的根的分布問題，可等價轉化成二元一次不等式組，也就是線性規劃的約束條件，而所求的分式可以轉化為斜率型目標函數研究.

例4定義在R上的奇函數y=f（x）為減函數，若m，n滿足f（m2-2m）+f（2n-n2）≥0，則值范圍為______.

解析：由于函數為奇函數且為減函數，故由f（m2-2m）+f（2n-n2）≥0得f（m2-2m）≥f（n2-2n），即m2-2m≤n2-2n，（m+n-2）（m-n）≤0，畫出可行域，如圖2所示，由圖可知

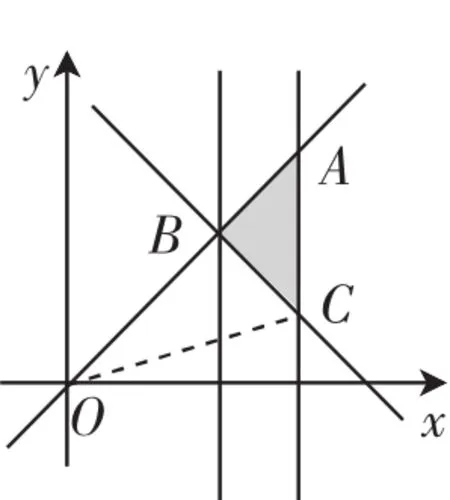
圖2

本題利用函數的單調性與奇偶性，將不等式的問題轉化為線性規劃問題來求解，同樣需要通過轉化將約束條件找出.

這組例題考查的是學生轉化思想的熟練運用，題中沒有明顯的二元不等式組出現，而是藏在各種背景的數學知識中，要運用等價轉化將約束條件尋找出來，就成為一個線性規劃問題了.

三、題目中有約束條件，但約束條件不常規

1.約束條件非線性

例5 在平面直角坐標系xOy中，A（-12，0），B（0，6），點P在圓O：x2+y2=50上，若≤20，則點P的橫坐標的取值范圍是_______.

本題結合直線與圓、平面向量的知識，可以用線性規劃知識解決.在研究過程中發現，動點所在區域并不是我們一般常規的線性約束條件所得到的邊界直線圍成的一塊區域，而是一段圓弧.我們都知道，目標函數非線性的還有斜率型和距離型這兩種常規類型，但是約束條件非線性的情況相對來說學生沒有那么熟悉，只要弄清楚動點的運動軌跡，其實仍然可以運用線性規劃的方法解決.

2.約束條件為多元問題

例6 已知△ABC的三邊分別是a，b，c，2a＞b+c，2c＜

例7 已知正數a，b，c滿足：5c-3a≤b≤4c-a，clnb≥a+clnc，則的取值范圍是____________.

作出（x，y）所在平面區域，如圖3所示.設y=ex上切點為則切線方程為，將原點代入得x0=1，求出y=ex的切線的斜率為e，即的最小值為e.

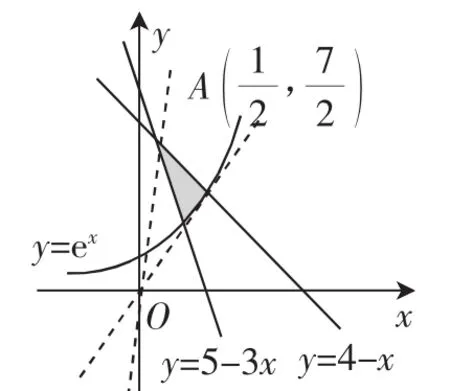
圖3

此題表面上是關于不等式的基本問題，可是深入分析發現簡單的不等式性質不夠用.構造關于的不等式組，將三元一次不等式組化成二元，這樣就可以化歸為線性規劃問題進行解決.本題綜合性較強，既有多元變量需要處理，約束條件也有非線性的情況出現，對學生轉化與化歸思想運用的要求相當高.

線性規劃的本質是代數問題幾何化，利用圖像解決二元變量取值范圍問題，其核心思想是數形結合.在高考題中多與函數、不等式、平面向量等知識結合，以考查學生的綜合運用能力.只要我們認清其本質，不管其背景如何，與哪些數學知識綜合，有沒有明確給出約束條件，約束條件是否線性，變量是二元還是三元，熟練運用轉化與化歸思想，線性規劃作為求解二元變量取值范圍的基本手段之一，都是我們解決這類問題的利器.F