淺談運用課標新理念指導簡單分數應用題教學
劉曉陽
摘 要:在小學數學教材中,分數應用題是重要的組成部分。要做好分數應用題教學,需要教師重點指導分數乘、除法意義的認識,培養學生解題策略,學會對結果合理性驗證,激發學生積極主動發現、探究問題,獲取知識,培養他們思維的準確性、靈活性、深刻性及創造性。
關鍵詞:新理念;分數應用題;小學數學
中圖分類號:G62 文獻標識碼:A 文章編號:1673-9132(2018)07-0021-02
DOI:10.16657/j.cnki.issn1673-9132.2018.07.012
在小學數學教材中,分數應用題是重要的組成部分。簡單的分數應用題又是這部分的基礎。做好分數應用題教學,不僅能培養學生的分析、比較和綜合能力,更能培養他們思維的準確性、靈活性、深刻性及創造性。因而,《課程標準》(以下簡稱《課標》)對簡單分數應用題教學提出要求:“使學生能夠解答比較容易的一至二步計算的分數應題,能夠綜合運用所學知識解決比較簡單的實際問題。”現就談談本人運用《課標》新理念指導簡單分數應用題教學的一些做法。
一、密切聯系生活實際,重點指導分數乘、除法意義的認識
聯系生活學習數學,培養學生的數學情感,是《課標》的重要理念之一。尤其是分數應用題乘、除法,知識抽象性較突出,更應與學生所熟知的生活知識聯系起來。故而在安排例題和進行單項訓練時,題目內容均要來源于學生的生活實際。例如,教學分數乘整數,我根據農村學生的認知特點,提問這樣一個問題:鐘叔等人在村里規劃一塊地蓋大棚種蔬菜,每間大棚占這塊地的2/15,6間共占這塊地的幾分之幾?讓學生在學習中能體會到數學就在我們每個人身邊,從而感受到數學的趣味和作用,增強應用數學的意識和學習數學的信心。
二、培養學生解題策略,教授解答簡單分數應用題的教學思想和方法
《課標》把學生獲得基礎的數學思想方法當作數學學習的一個重要目標。它能幫助學生在掌握分數應用題知識、形成解題能力的同時,學會科學地思考問題,探索發現解決問題的規律與途徑,使數學學習變得更加容易理解和掌握。分數應用題的解題策略可從以下幾個方面進行思考。
(一)指導準確判斷單位“1”,掌握標準量
準確判斷單位“1”是分數應用題的解題關鍵。解答分數應用題之前應先準確判斷單位“1”。單位“1”就是標準量,也是被比的量。在教學中可安排如下題目讓學生進行單項訓練:找出下面各題的分率:1.“沈清把一條長3/4米的繩子剪下1/4,剪下多少米?”2.“一段路,上午修全長的1/5,下午修3/4千米,還剩2千米沒修,這段路長多少米?”通過訓練,使學生明白了只要讀懂這道題的分率句,就確定了單位“1”。
(二)運用線段圖,幫助理解題意
數學教學是探索性的數學活動,學生的學習過程是一個發現問題、收集信息、處理信息和得出結論的過程。針對分數應用題數量關系比較抽象的特點,教學時,在指導學生找準單位“1”后,可用畫線段圖的方法進行分析,探索出數量關系及其解題思路。
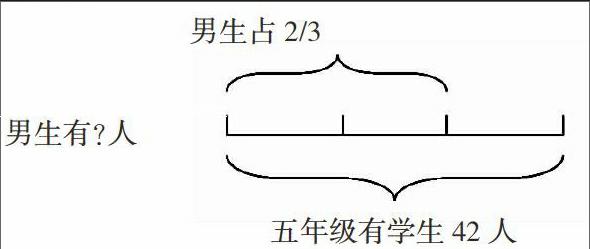
例1.“學校五年級有學生42人,其中男生占2/3,男生有多少人?”題目中單位“1”是五年級學生42人,求男生有多少人可畫圖如下:
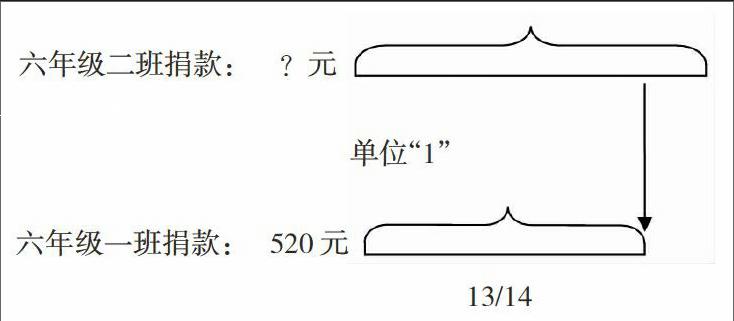
例2.“在一次獻愛心活動中,六年級一班共捐款520元,是六年級二班的13/14,六年級二班捐款多少元?”題目中單位“1”是六年級二班的捐款數,是所求問題。可畫圖如下:
這樣,分數應用題中的數量關系便直觀、具體地呈現于學生的面前。通過以上形式的反復練習,學生在處理信息方面就更加熟練,并且能在探索中自己得出結論,得出新知。
(三)指導掌握解答簡單分數應用題的模式
簡單分數應用題一般分三種類型:⒈“求一個數是另一個數的幾分之幾?”⒉“求一個數的幾分之幾是多少?”⒊“已知一個數的幾分之幾是多少,求這個數。”這三種類型中,第1種通常用“一個數÷另一個數=多少”來解答;第2種可運用分數乘法的意義“用一個數×幾分之幾=多少”來解答;第3種利用除法的意義“用多少÷幾分之幾=這個數”來解答。其中第1、2類中的單位“1”都是已知的,用乘法算。而第3類中的單位“1”是未知的,用除法算。如上兩例,例1中的單位“1”是五年級學生人數已知有42人,用42×2/3=28(人);例2中的單位“1”是六年級二班捐款數未知,根據分數除法的意義(已知六年級二班捐款數的13/14是520元,求二班捐款多少元?)用520÷13/14=560(元)。由此,還可以引導學生歸納出兩個公式:對應量=單位“1”×對應分率;單位“1”=對應量÷對應分率。
(四)教會學生用方程解分數應用題
為培養學生靈活地分析、解決問題,有時分數應用題可用方程解,學生較容易接受。如例2中,六年級一班捐款是二班13/14,根據分數乘法的意義,用二班的捐款×13/14二班的捐款520元,可解:
設六年級二班捐款x元
x×13/14=520,x=520÷13/14,x=560
根據求一個數是另一個數的幾分之幾,可解為:
設六年級二班捐款x元
520÷x=13/14,x=520÷13/14,x=560
三、結合《課標》精神,教會學生檢驗
一道應用題解答完畢,有的學生心里很盲目,不知自己做得正確與否,這是平時不會檢驗或沒有養成檢驗習慣的結果。《課標》指出:“數學教學時,要讓學生主動地進行觀察、實驗、猜測、驗證、推理與交流等數學活動,檢驗是解答應用題的最后環節。”分數應用題的檢驗可把求得的答案代入題目的已知條件中,看與題目的另外條件是否相吻合。檢驗的方法可以有多種,因人而異,因題而異。如上例2檢驗:方法1,520÷560=520/560=13/14;方法2,560×13/14=520(元)。通過檢驗既能培養學生“自主學習、探究”的學習方式,教會學生學習,又能使他們獲得成功后的喜悅,增強信心。
參考文獻:
[1] 魏思文.新理念指導下分數應用題教學初探[J].新課程導學,2012(27).
[2] 李紅.用新課標基本理念指導小學數學教學[J].小學教學參考,2002(12).endprint

