教之以法 授之以漁

江蘇省昆山經濟技術開發區高級中學 劉勝男

“授人以魚，不如授之以漁。授人以魚，只救一時之及；授人以漁，則可解一生之需。”——《老子》

“一個不好的教師奉送真理，一個好的教師則教人發現真理”，這是德國教育家阿道爾夫·第斯多惠的名言。意思是說，在教會學生知識的同時，更應該教會學生學習的方法。這樣循序漸進，落實從知識到方法的傳授才是教師應該真正做到的。

授之以漁，就要多用啟發式教學法。古希臘偉大的哲學家蘇格拉底開創的“問答法”，就完美演繹了啟發式教學法的過程。在向學生介紹某個概念時，他并不直接告訴學生概念的內容，而是先提出問題，讓學生回答。如果學生答錯了，他也不直接糾正，而是提出另外的問題，引起學生的思考，從而一步一步、循序漸進地慢慢找到正確的結論。在學習的過程中，學生是學習的主體，要想使學生在基礎知識和基本技能的學習中獲得更好的效果，就要充分地發揮學生的自主性和主動性。我們在教學上，要多用啟發式教學法，不能直接把知識拋給學生去被動接受，而是要啟發他們自己發現結論。

比如，在研究切線長的最值問題時，可以先讓學生練習定圓外的一個定點所引出的切線長，如，例1：從圓外一點P（2，3）向圓引切線，則切線長為___________。

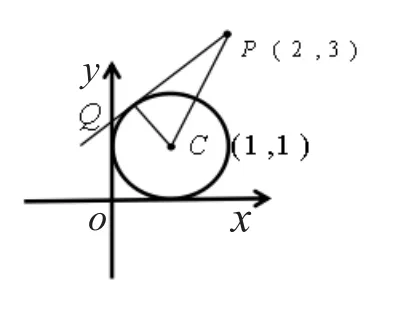
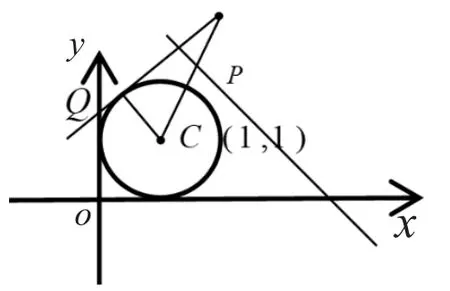
學生都可以順利解決問題，然后引出變式。

變式1：由直線x+y=5上一點向圓引切線，則切線長最小值為_____。

在學生面對動點問題感到難以解決時，啟發學生進行思考，同樣是計算切線長，上題我們如何解決的？如何轉化切線長？使學生發現，無論動點、定點，一樣利用勾股定理，將切線長轉化為兩點間距離平方與半徑平方的差來計算。這樣學生得到啟發，雖然變式中的切線兩端均為動點，但動點之間的距離，可以轉化成一個定點（圓心）與一個動點（直線上的點）的距離來解決，從而問題轉化為研究一個定點與定直線上的一個動點如何距離最小的問題。到此為止，學生都易于發現問題最終轉化為圓心到直線距離的問題。在此基礎上，教師還可以再舉出其他例子，繼續延伸，繼續啟發學生自己找出解決方案。

通過前面例子，讓學生自己嘗試，自我啟發，在諸多的變化過程中，如動直線l1，是否有什么關系是“定”的？動的垂足P，是否有什么關系是“定”的？在學生實現不了的時候，再給以啟發，所謂“不憤不啟，不悱不發”，學生自會逐步學會從跟隨教師的啟發進行思考，到學會在遇到困難時，實現自我啟發。多用、善用啟發性教學法，從啟發學生開始，慢慢讓學生習慣于自我啟發，才能慢慢達到“授之以漁”的效果。

授之以漁，就要實踐因材施教的教育理念。因材施教，就是根據不同的學生，選擇不同的材料或者不同難度的例子，讓各個層次的學生都容易接受和理解。只有依據學生理解能力的不同，對不同的學生運用不同的例子，才能讓他們更易于掌握知識，學會方法，理解精髓。

比如直線過定點的問題，不同學生從不同的題目開始引導。基礎較差的同學，可以從下述例子的第（1）小題開始思考；基礎好的同學，可以從第（3）小題開始思考；基礎非常好的同學可以直接嘗試第（4）小題，然后讓學生自行總結，定點為何為“定點”？如何才能確定定點？

例3 （1）y=kx+1過哪個定點？

（3）y=kx+3-2k過哪個定點？

（4）若a，b，c成等差數列，則直線y=ax+by+c過哪個定點？

在不同的學習場合，不同類型、不同能力水平的學生，其學習表現也是不盡相同的。需要教師憑著自己的經驗、智慧靈活地設計出因材施教的教學實例和教學方法。實踐因材施教的教育理念，可以讓每位同學都找到自己的參與感，最大限度地讓更多學生在課堂中學會處理問題的方法，全面實現“授之以漁”。

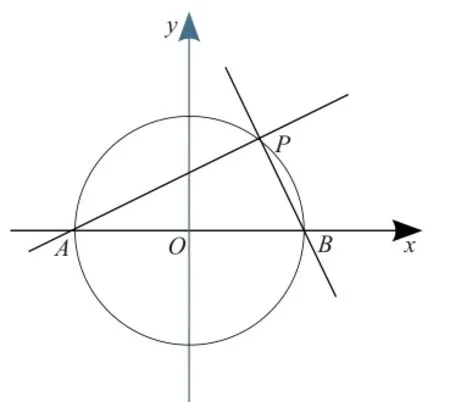
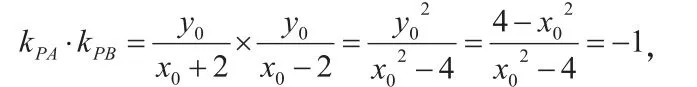
有助于接下來的探究給他們以啟發，接下來讓他們實踐探究：

學生自行經歷這些由淺入深，循序漸進的探究過程，慢慢養成自行思考、動手嘗試的習慣，從問題的發現，到思考、探究，進而自行解決問題，這是實現“授之以漁”的必經之路。陶行知先生說過：“教學做是一件事，不是三件事。我們要在做上教，在做上學。不在做上用功夫，教故不成為教，學也不成為學。”在平時的教育教學過程中，我們要踐行“教學做合一”，堅持給予學生付諸實踐的機會，養成探究的習慣，才能真正實現“授之以漁”。

第斯多惠還曾說過，任何真正的教學不僅是提供知識，而且是給予學生以教育。作為一名優秀的數學教師，僅僅“授人以魚”是不夠的，而當我們深刻理解到“授人以漁”的本質，才能教出更好的學生。從端正學生態度、善用啟發式教學法、實踐因材施教的教育理念、養成探究的習慣三個維度去落實“授之以漁”，只有這樣，才能真正地落實素質教育，而我們的教育改革才能走得更遠。