淺談數學知識在高中物理解題中的應用
柴子渝
摘 要:高中物理課程具有綜合性強、聯系性強、實驗性強等特征。基于課程的特殊性,許多物理定律都是通過數學公式得以體現的。因此,我們在解題的過程中需要結合數學相關知識,提升自身的的物理解題能力。基于此,本文以學生的視角為出發點,根據自身的實踐經驗,針對數學知識在物理解決中的應用進行了深入的分析和探討。
關鍵詞:數學知識;高中物理解題;應用;實踐
數學思想方法已經在高中物理解題中得到了廣泛的應用,并取得了較好的教學效果。因此,想要在高中物理解題過程中靈活應用數學知識,則需要深入學習數學思想方法和數學知識理念,來解答抽象的物理問題。以下對此展開了詳細的敘述,希望對于我們有所啟示。
一、注重從數學角度分析物理相關概念和公式
抽象的物理概念和公式對于我們來講是無疑是最難理解的部分。而解題能力的提升則是建立在充分理解物理概念和公式的基礎上。想要在解題中適時的運用數學知識,則需要我們在日常的學習過程中以數學角度為出發點來理解抽象的物理概念和公式。從而提升我們的數學應用意識,并為之后的物理解題思維提供了保障。文章以《平拋運動》為例:我們需要在熟讀概念后,增強整體上的理解。即運動軌跡就是拋物線。但是這種理解具有一定的片面性,有些同學對于其深入的內涵并沒有徹底的明白。究其原因,主要與有些學生沒有通過聯系數學知識進行概念的理解。在我們進行習題的計算時,首先根據以往教師的指導,對 和 兩個公式進行推導,得出軌跡方程 。其次,在運用數學角度理解相關的公式,并將 作為非變量,運用字母 進行代替,從而得出公式 。而這個公式對于我們來講應該感覺不到陌生,其正是我們所學的數學知識,即二次函數的公式。由此可見,這種計算的方法不僅能夠讓其他同學深刻的理解到平拋運用的本質和特征,還能夠提升數學應用知識的意識。從而讓學生在平時的物理解題過程中運用數學角度理解物理的相關概念和公式,為提升我們的物理解題能力奠定基礎。
二、總結常見數學思想及方法的運用,提升數學應用能力
首先,對于一些典型、易出現錯誤的題型進行我們需要進行重復的講解,并在解題的過程中找出自身的不足。其次,需要靈活的運用數學思想和方法,解答物理習題中存在的問題。其中最為常見的數學思想主要包括:函數換元、數形結合方法等。以下詳細介紹了這兩個方面:
(一)函數換元的應用
復雜的運算是物理解題過程中需要引起重視的部分。而函數換元具有換復雜為簡便的優勢,很多物理習題中涉及到了很多的函數換元的應用,并以此為切入點,讓我們進行應用和理解。可見,這種數學方法是值得我們學習和掌握的。其對于我們解題具有很大的幫助。例如:解答以下習題時:小張和小李放學后想要去超市買文具,他們分別于A、B兩點相向而行,均可看做勻速直線運動。同時,小李同學要比小張同學玩晚走2分鐘,然而在到達超市時,小李同學卻比小張同學多走了400米的路。求兩人在超市相遇的那刻起算,小張在11分鐘到達B地,小張5分鐘到達A地。兩人之間的距離為多少?
例題分析,首先,假設兩人在相遇后的位置距離A地為X,則小李的速度為 ;小張在相遇后還需要走 ,其速度為。于是得出方程式為: 然后將 用字母1所替代,計算的公式就大大減少,同學們就能夠很快的算出兩者之間的距離。
(二)數形結合的方法
物理問題在解答的過程中,有很多運用圖形來表示物理量的題型。因此在進行物理題目講解時,應該增加這方面知識的訓練和理解。以提升數學解題方法的應用。例如:在解決物理習題時,我們可以通過運用畫圖的方式,增強物理知識的理解。然后在根據解決數學問題的方式,在圖中標志出具體的數字,并通過數形結合的方法明確考查的知識,從而進行相應的解答。這種結合圖形的方法,能夠使我們一目了然的找出抽象的物理知識難點,并根據圖像的表示,使得問題更加簡單明了。
三、應用極限值求解物理問題
函數作為數學的重中之重,其對于提升的解題效率具有很大的幫助。例如:我們在學習物理電路相關知識時,運用極限求解方法,解答以下例題中的問題。
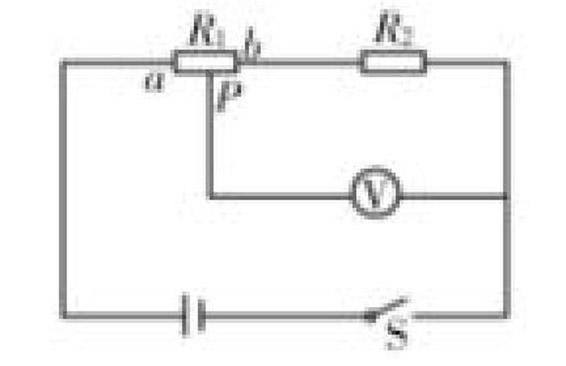
例題展示:滑動電路中的變阻器 的最大阻值為400Ω,定值電阻為 =500Ω,這個電路中的電源電壓保持在 。如果將滑動變阻器中的a滑動至b,那么電表的變化范圍是怎樣的呢?如圖所示:
解題的思路:運用極限求解方法,得出 具有兩個極值,在P到達a時,其最大值為400Ω,這時我們知道電壓表中所測出的數值為 、 中的電壓。也就形成的總電壓U,即為 ,在P到達b端時,可知它的最小值為0,這就很容易測出電壓表的變化范圍。
數學知識在物理解題的過程中得到了廣泛的應用。因此,只有學生們在課堂、課下進行積極、仔細的學習,并將數學知識融入物理習題中,這樣才能讓學生應用數學知識解決物理問題的意識和能力。
參考文獻:
[1]張嘉璇.淺談數學知識在高中物理解題中的應用[J].高考,2018(32):248.

