求數列通項公式的另一方法
安徽省合肥市廬江裴崗中學 邢寶清
數列一直是高考中的重要內容,無論是全國高考試卷還是自主命題的試卷,數列都是考查的重點,同時,數列對提高中學生思維,強化中學生邏輯推理能力,都起到了積極的作用。而求數列的通項公式又是此內容的重點,在近幾年的高考中,有關遞推數列的通項公式方面的試題越來越多,難度越來越大,仔細研究大量的數列試題,其中大部分試題的解題方法無非是把它們轉化為等差數列或等比數列來解,而轉化的常見方法是待定系數法,但有時轉化過程卻使同學們感到很難發現其特殊的情況,現專門探討一種求遞推數列的通項公式的方法——特征根法,希望能給同學們一些啟迪。特征根法是解常系數線性微分方程的一種通用方法,數列中一階或二階線性遞推公式,即差分方程也可用特征根法求通項公式。
給出定理:若數列{an}滿足an+2=pan+1+qan,其特征方程為x2-px-q=0。
若其方程有兩個不相等的根(稱作特征根)s1、s2,則其中常數c1,c2的值由初始值a1、a2的值確定。
若方程有兩個等根,即s1=s2,則an=(c1n+c2)sn,其中,常數c1,c2的值由初始值a1、a2的值確定。
證明:∵an+2=pan+1+qan,設存在實數r,s使an+2-ran+1=s[an+1-ran],
所以an+2=(s+r)an+1-sran,令p=s+r①,q=-sr②,則 s,r為一元二次方程x2-px+q=0的兩個根,
若r≠s,則方程組①②有解為(s1,r1)和(s2,r2),
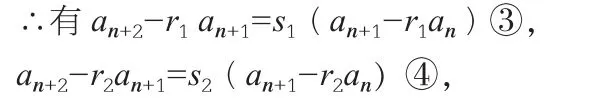
由③得{an+1-r1an}是以a2-r1a1為首項,以s1為公比的等比數列,則其通項公式是
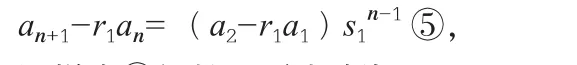
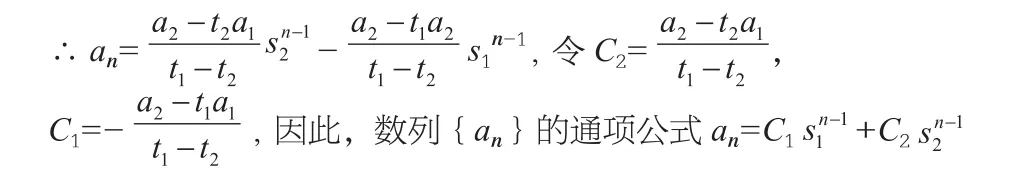
若s1=s2,易得an=(c1n+c2)sn證明(略)。
例 1 已 知 數 列{an} 滿 足 a1=1,a2=1,an+2=5,an+1-6an,n∈N+,求數列{an}的通項公式。
分析:上述數列的遞推公式給出的是連續三項之間的關系,若用特征方程的特征根來解,則較為方便。
解:上述數列的特征方程為:x2=5x-6,那么其方程的根為x1=3,x2=2或x1=2,x2=3。于是,可以設an=c1x1n+c2x2
n(*),即得an=c12n+c23n,然后將a1=1,a2=1代入(*)解得從而可得an=2n-3n-1。
例2 已知數列{an}滿足a1=2,a2=3,an+2=3an+1-an,n∈N+,求數列{an}的通項公式an。
分析:上述數列的遞推公式給出的是連續三項之間的關系,若用常規方法,就要對遞推公式進行變形,使它能成特殊數列,然后利用特殊數列的有關性質來解,雖然可以解出,但顯得比較煩瑣,因此可以用特征方程的特征根來解較為方便。
解:由題意可知,此數列的遞推關系符合其特征方程x2=3x-1,可解得其根為于是可設所求數列的通項公式為然后將a1=2,a2=3代入(*)可解得因此數列的通項公式為
以上是對于特征方程有兩個不同的特征根的情況,求此類通項公式極為方便,若特征方程有重根,即有兩個相等的特征根時,又是如何來解呢?這時也可以用上述公式,相對于有兩個不等根還要簡單一點。
例3 已知數列{an},若a1=3 , a2=5 且an+2=4an+1-4an,求數列{an}的通項公式。
分析:此數列可以將遞推公式進行變形,使之成為新的特殊數列(等比或等差),然后利用特殊數列的特征來解,但是那要進行多次變形才能求出,若用特征根法解就顯得簡便一些。
解:設該數列的特征方程為x2=4x+4,可得方程有兩個相等的實數根x1=x2=2 ,因此可設數列通項公式為 an=(c1+nc2)2n(*),然后將n)2n-2。
總之,求數列的通項公式的方法是多種多樣的,高中學生應該從給定的已知條件中善于發現其規律,靈活利用不同方法解決有關問題,這對學生打開思路,鍛煉學生的思維有很強的促進作用。

