中考數學中常見的圖表信息型問題
江蘇省海門市能仁中學 沈永平
所謂的圖表信息題,就是指通過圖象、表格來獲取信息,從而達到解決問題目的的題型。該類題型的常見問題有:(1)圖形信息題;(2)圖象信息題;(3)表格信息題。這些圖形與表格來源廣泛而且形式靈活,但都可以轉化為數學模型,由此可見,該類題型的難點在于怎樣合理地建立數學模型,從而將生活中的問題轉化為數學問題進行解答。
一、圖形信息題
所謂圖形信息題,指的就是幾何題,但并不是簡單的幾何題,其中往往還包含了找規律。因此,探索規律是解決圖形信息問題的關鍵,探索規律時先要有敏銳的觀察,再進行合情推理。此外需要注意的是,在觀察圖形時應該從圖形的個數、形狀以及圖形的簡單性質等特點入手,這樣往往會很容易發現其中規律。
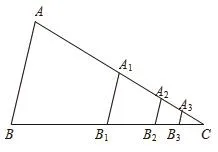
解析:∵A1、B1分別為AC、BC的中點,……第n個四邊形的面積為
點撥:此題運用三角形的中位線、相似三角形的性質等幾何知識解決代數的計算問題,其體現了數形結合的思想。另外,從本題的解析過程中,我們可以清晰地看出此題是從一般到特殊進行逐步歸納,體現了歸納類推的思想。
二、圖象信息題
解答圖象信息問題的關鍵是化“圖象信息”為“數學信息”,要善于從圖象的形狀、位置、發展變化趨勢等有關信息中獲得啟示。因此,認真讀圖,捕捉有效信息,往往對解題會起到事半功倍的效果。
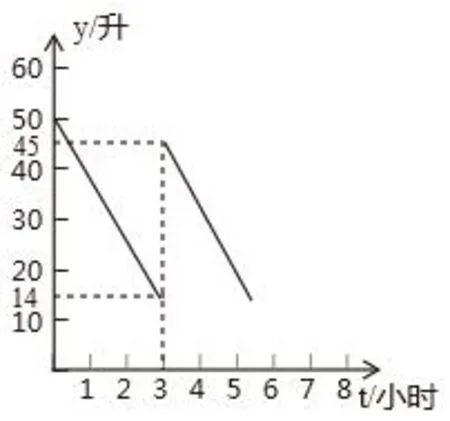
例2 小成去某地旅游,汽車出發時有油50L,出發一段時間后,在加油站加了一些油,油箱中的剩余油量y(L)與行車時間t(h)之間的關系如圖所示。
(1)求加油前的剩余油量y(L)與行車時間t(h)的關系;(2)若小成的車速始終為70km/h,而且加油站距離目的地還有210km,請問小成能否到達目的地?
解析:(1)設y與t的關系式為y=kt+b(k≠0),由圖象可知,將(0,50)、(3,14)代入,解得:k=-12,b=50,故其關系式為;y=-12t+50。(2)由圖象可知,汽車每小時要用油(50-14)÷3=12(L),因此小陳到達目的地還需要用油210÷70×12=36(L),而油箱里有45L的油,因此小成可以到達目的地。
點撥:解答此類題目,需要注意兩點:(1)注重整體的閱讀,對題干所給出的材料及圖表資料等有一個整體的了解,尋找有效的信息;(2)注重數據分析:分析某些變化的數據,其往往是解題的突破口所在。此外,還需要著重注意的是圖象中的一些特殊點和圖表中細節的變化,其往往對解題有提示作用。
三、表格信息題
解答表格信息題的關鍵就是從表格中發現兩個變量之間的對應關系或數字之間的規律,在探索兩個變量之間的關系時,注意是否均勻變化或兩個變量的一對對應值是否不變,從而建立數學模型,歸納出相應的關系式。
例3 土地的總面積為10畝,其中A類植物的種植面積占總面積的60%。下表為各農作物的產量與售價的對應關系。

A B C畝產量(千克) 400 600 220銷售單價(元/千克) 2 1 2.5
設B類植物的種植面積為x,三種農作物的總售價為y,寫出y與x的關系式。
解析:因為總面積為10畝,設B類植物的種植面積為x,又因為A類植物的種植面積占總面積的60%,所以其面積為6畝,C類植物的種植面積為(4-x),此時通過分析表格數據,即可得:y=400×2×6+600x+220×2.5×(4-x)=50x+7000。
點撥:從閱讀題干中,我們很難發現此題考查的是什么知識點,但從此題的解題過程中我們會發現,只要認真審題,跟著題目的意思走,很容易就會發現此題考查的是一次函數,從而我們可以看出,此類題型具有很大的迷惑性。因此在解答該類題型時,一方面要認真審題,分析表格數據,另一方面不能有畏難情緒。
綜上所述,從上文所給出的例題我們會發現,圖表信息型題有一個共同的特點,就是其考查的知識點實際上比較簡單。簡而言之,就是將一些我們常見的知識點(例如:幾何、函數、統計等)通過一些方法(例如:與實際問題結合等)包裝一下,從而給人一種耳目一新的感覺。因此,在解答此類題型時,要通過讀圖、分析表格等手段發現題目的實質,然后利用合適的數學知識點進行解題。

