求函數值域的方法探討

云南省曲靖工商職業技術學校 陳 繼

高中數學中，函數值域問題屬于函數的綜合性問題。雖然高中學生具備一定的邏輯思維能力，但是由于函數值域的題型和求法很多，如果學生沒有掌握有效的求值域的解題方法，解題中就難以獲得準確的答案。高中數學中，求函數值域是高考數學的重點和難點。本論文針對最值問題的解題方法展開研究。

一、高中函數題的解題中采用配方法求函數值域

在數學解題中采用配方法，就是把一個解析式利用恒等變形的方法，把其中的某些項配成一個或幾個多項式正整數次冪的和的形式。通過配方解決數學問題的方法叫配方法。其中，用得最多的是配成完全平方式。配方法是數學中一種重要的恒等變形方法。配方法最主要的目的就是將一個一元二次方程或二次多項式化為一個完全平方式，以便簡化計算，使變量減少，使問題簡化。

比如，求函數值域的數學題：y=7- 4sinxcosx十4cos2x-4cos4x，求函數的最大值和最小值？

對于這道函數式的解題方法有兩種：

第一種解題方法：

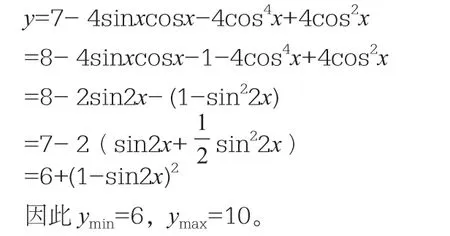
第二種解題方法：

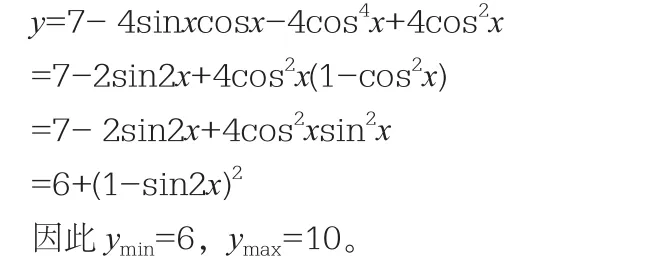
這道函數題的主要考查點是三角恒等變換，同時還對二次函數的相關知識和三角函數的相關知識進行考查。在高考數學題中會經常出現這種類型的數學題，屬于常規的知識點。

二、采用換元法求函數值域

換元法就是以新變量代替函數式中的某些量，使函數轉化為以新變量為自變量的函數形式，采用換元法求函數值域的方法，就是使抽象復雜的函數變得更為直觀、簡單、形象，變為普通常見的函數，從而簡單快速地求出函數的值域，但是換元時一定要注意所換“元”的取值范圍，它會影響函數的值域。比如，求函數的值域，采用換元法對原函數進行轉化，轉變為某個變量的二次函數，之后就可以將二次函數的值充分利用起來，對原函數的值域加以確定。

對于這道數學題，如果采用換元法，具體解題如下：

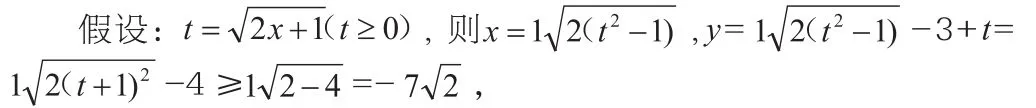
利用換元法求函數值域，一定要注意函數的結構形式，要明白哪種結構類型的函數可以用換元法，教師要引導學生仔細觀察，認真審題。高中學生雖然具備一定的邏輯推理能力，但是習慣于解題中運用形象思維思考，用換元的方式解決數學問題，可以使得在數學解題中轉換為學生已經掌握的數學知識。復雜的函數題通過換元后可以替換常見熟悉的函數，從而使學生的豐富想象力被激發起來，從已經掌握的知識出發理解數學題中所提出的問題，使學生在解答數學問題的時候，讓復雜抽象而難以理解的數學題變得簡單直觀，容易理解，使復雜問題簡單化，從而提高學生的解題能力。

三、采用判別式法求函數值域

在利用判別式法求函數值域時，也要弄清函數的結構，y是關于x的分式型二次函數，就是把函數y=f (x) 看作一個關于x二次方程，“x的二次方程 y=f (x)有實數解，判別式必須大于等于0，解一個關于y的一元二次不等式，從而求出y的取值范圍。”判別式法是求函數值域的一個非常重要的方法，用于分式型二次函數的函數值域求解。

解：x2+x+1=(x+12)2+34＞0，所以函數的定義域是R。

去分母：y(x2+x+1)=x2-2x+1，得：(y-1)x2+(y+2)x+(y-1)=0。

當y≠1時，由Δ≥0得0≤y≤4；

當y=1時，將其代入方程中得x=0。

得出原函數的值域為[0，4]。

總之，函數值域的求法多種多樣，根據函數結構類型掌握一定的函數求值域方法，有助于提高學生解題準確率，有助于培養學生的解題速度，有利于學生對函數知識的理解。