線性規劃問題的常見典型錯誤及應對策略*

王淼生 李寅童

福建省廈門第一中學 (361003)

線性規劃在高中數學中占有極其重要的地位，其本質就是最優化的具體模型之一，是高考及競賽中的重點、熱點、難點，查考形式以選擇題、填空題居多．隨著高考考查重心從知識立意向能力立意轉變，因此線性規劃試題對能力要求越來越高．線性規劃相關問題常常成為命題專家在截距、斜率以及距離(兩點間距離與點到直線的距離)等知識網絡交會處命制高質量試題的青睞區．然而，線性規劃相關試題知識點多、變形技巧高、解答靈活性強、思維跨越度大，這些特點導致學生出現解答不嚴謹，或審題有偏差，甚至有些問題無從入手．坦率地講，有些試題連教師都出現瑕疵，甚至束手無策．本文擬通過具體案例來剖析出現錯誤的原因及應對策略，不當之處，敬請批評指正．

1.因任性習慣而導致錯誤

案例1 若α、β是2x2+2ax+b=0兩根，α∈[0，1]，β∈[1，2]，則a2+b2的最小值為 ．

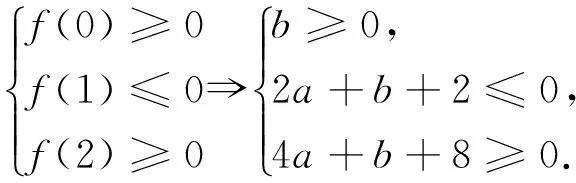
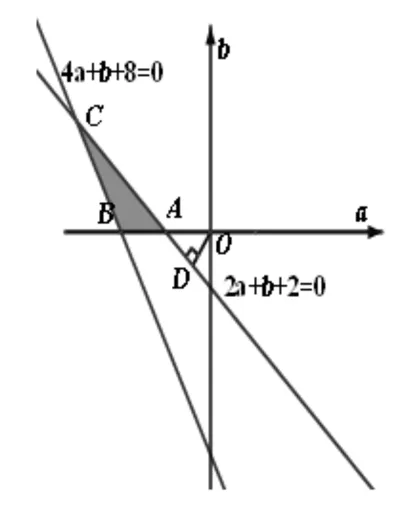
圖1

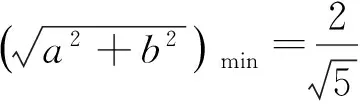
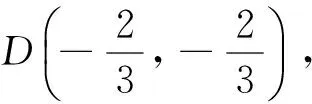
2 因忽視“約束”而導致錯誤

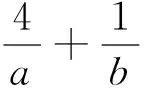
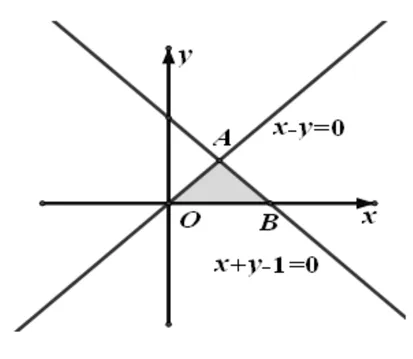
圖2

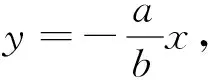
3 因概念不清而導致錯誤

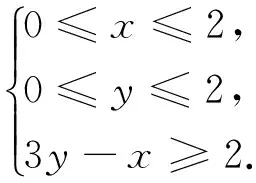
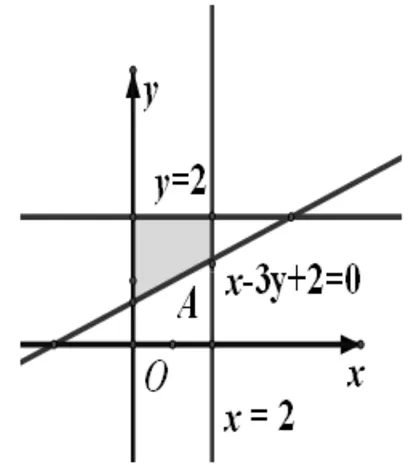
圖3

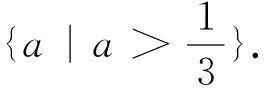
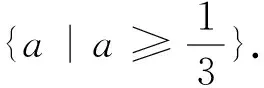
值得指出的是：案例3還有一種典型的錯解，誤以為z的最大值就是直線截距的最大值．其實由變形可得y=ax+(-z)，由此可知z的最大值恰好是直線y=ax在平移過程中截距的最小值，這是學生剛剛接觸線性規劃最容易犯的錯誤．

4 因審題膚淺而導致錯誤

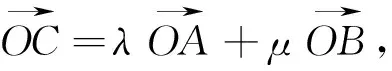
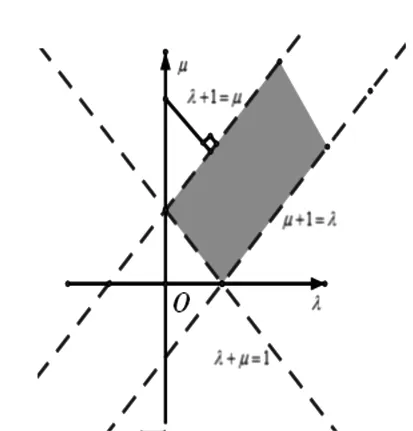
圖4

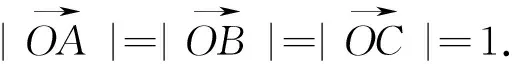
錯因與應對策略：案例4為某地一道模擬試題，絕大部分學生審題膚淺、理解不透而根本看不懂題意．由向量加法聯想到三角形，這才是解決問題的突破口，再利用三角形最簡單性質：兩邊之和大于第三邊，構造λ與μ之間關系，從而轉化為熟悉的線性規劃的距離問題．

值得指出的是：請讀者仔細體會上述案例1與案例4的區別．盡管都是點到直線的距離，但案例1是因為垂足點根本不在可行域而導致錯誤，案例4則是因為邊界為虛線的原因而導致取不到最小值．

5 因不會“壓縮”而導致錯誤

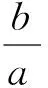
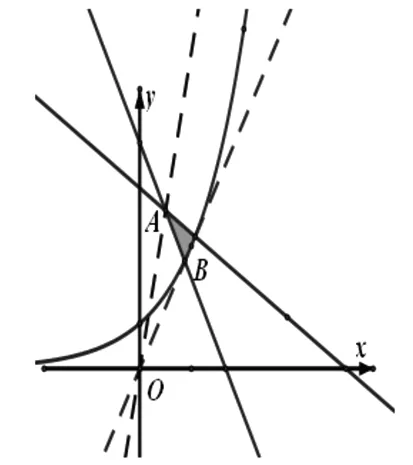
圖5

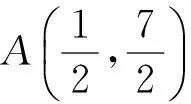
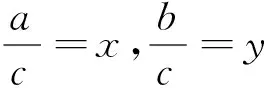
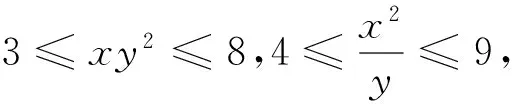
本題作為當年填空題壓軸題，是當年高考所有線性規劃試題中一道靚麗風景線，也是近年來線性規劃方面高質量命制試題的典范．然而，絕大部分學生不知所措，根本不會借助“媒介”手段：“壓縮”而成為失分重災區．一線教師不得不捫心自問：我們課堂教學是否與新課改精神吻合？我們是否在傳授知識的同時更加側重能力培養及思維品質優化？對不等式頗有造詣的安振平先生多次提到代數變形是一種重要能力，也是數學基本功底的具體體現．

6 因不善轉化而導致錯誤

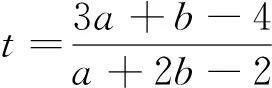
解答：由已知條件可得

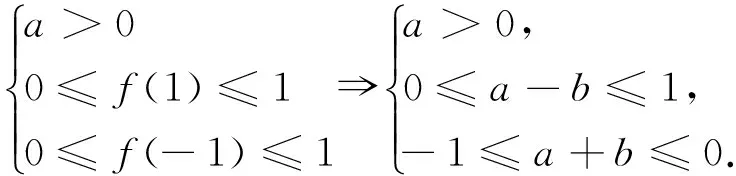
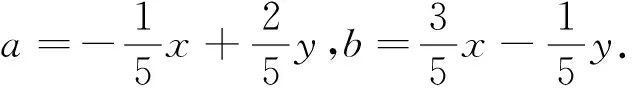
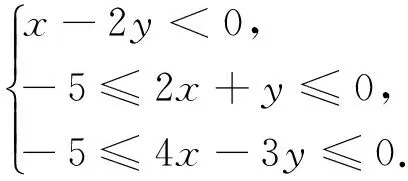
錯因與應對策略：高中階段線性規劃主要涉及截距、斜率及距離等三大類問題．然而，表面上案例6似乎與上述三大類問題毫無關聯，學生不得不知難而退．對于線性規劃問題緊緊盯住三大類型，通過轉化與化歸，使得問題向三大類型題靠近，這是解決問題較為有效策略．案例6說明：數學解題離不開基本題型與套路，心中沒有儲存必備、基本題型，在心情緊張、時間短促的考試氛圍下，寸步難移，必敗無疑．

7 因分類不全而導致錯誤

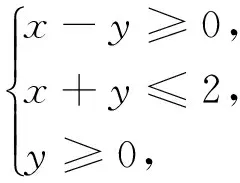
A．3B．2C．-2D．-3

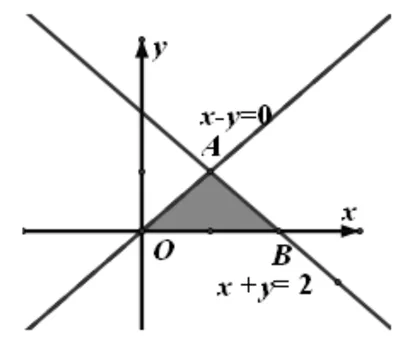
圖6

解答：先作出可行域，如圖6所示．我們需要再作直線y=-ax，哪該如何作圖呢？需要我們首先分三大類，即a<0，a=0，a>0．

(1)當a<0時，此時直線斜率為正數，此時要么過(0，0)截距最大；要么過A(1，1)處截距最大，由此得到4=0，或4=a+1，這都與條件矛盾；

(2)當a=0時，此時y=z，此時在A(1，1)處截距最大，由此得到1=4，得到矛盾；

(3)當a>0時，此時直線斜率為負數，此時又需要分為三小類：

(ⅰ)當-a>-1，即a<1時，此時過A(1，1)處截距最大，即4=a+1，得到矛盾；

(ⅱ)當-a=-1，即a=1時，此時直線x+y=2的截距本身就是最大值，即2就是最大值，這都與條件矛盾；

(ⅲ)當-a<-1，即a>1時，此時直線平移經過點B(2，0)處截距最大，由此得到4=2a，即a=2．綜上所述，故選B．

錯因與應對策略：客觀地講案例7不算難題，遺憾的是學生幾乎都認為答案為A，其實不少課外教輔書也是如此．之所以出現上述錯誤，其主要原因在于手工畫直線時，沒有特別關注直線斜率的大小比較，即沒有對a>0再細分為三小類進行討論，也就是說直線傾斜程度成為此類錯誤的“罪魁禍首”．當直線斜率沒有確定時，分類討論勢在必行，而且分類必須徹底．隨著命題原則與理念的轉變，滲透數學思想方法已經成為共識，因此線性規劃問題中進行分類討論成為常態化，有利于培養思維的嚴謹性與批判性．

如果說上述案例4～案例7讓學生苦不堪言，那么有些線性規劃試題，不要說學生，就連教師也難免出錯．縱使給出答案，縱使用盡洪荒之力，絕大部分教師也是無能為力．

8 缺洪荒之力而導致錯誤

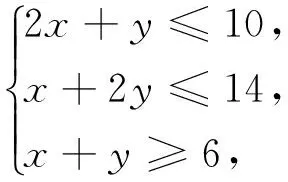
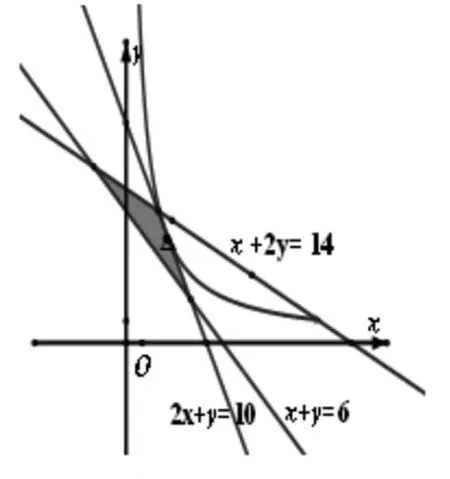
圖7

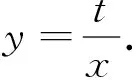
當然，解答線性規劃問題過程中出現錯誤的原因還有很多，囿于筆者功力淺薄，僅作拋磚引玉．筆者對三角問題常見的典型錯誤以及解答過程中出現的書寫不規范、論證不嚴謹等錯誤整理成文，有幸發表(詳見文[1]、文[2])并收到不少同行來信來電．正因教學需要、同行鼓勵，筆者思索三年完成本文，渴望與文[1]、文[2]形成系列論文，同時也希望有更多同行一起來探索其它模塊中常見典型錯誤及應對策略，比如，概率、函數、解幾、向量等．

[1]王淼生．三角問題常見的典型錯誤及應對策略[J]．中國數學教育(高中版)，2014(12)：48-52．

[2]王淼生．預防解題中不規范與錯誤的策略[J]．數學教育研究，2014(3)：64-66．