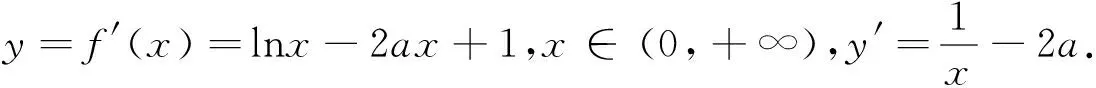一道含參零點問題課堂教學展示與拓展

段偉軍

甘肅省通渭縣第二中學 (743300)

函數零點是函數單元中的重要內容,它常常與方程、不等式等知識交匯,同時，函數的零點問題是高考的熱點與難點問題，全國高考理科2卷在16年、17年作為壓軸題出現，該類題難度大，區分度高.雖然通過高等數學的洛比塔法則研究發現部分函數存在漸近線，但人教A版(選修2-2)只是運用瞬時變化率來定義導數，并沒有涉及極限的符號，因此、部分老師在教學中用極限的思想解釋問題，顯然不符合教學的要求，要說明含參零點的存在性，除了研究函數的性質，還應借助于零點存在定理進行證明，即在指定的范圍內選取兩個自變量的值使其兩個函數值異號，由于參數的加入，所選取的兩個自變量與參變量有關，何種關系，何種形式不易獲得.

筆者通過平時的課堂教學觀察與教師的交流發現，此類題一直困擾著教師，不選取參數，解題不嚴謹，選取參數，無從著手，不知方向，方向不對，徒勞無功，而一些參考資料的解法過于復雜難理解，其實，這類問題是有規律可循的，只要探尋到這個規律，讓含參問題不再神秘難解，筆者通過一堂課的教學展示并拓展延伸，使問題柳暗花明、水落石出.

一、問題呈現

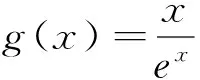
二、課堂展示

筆者在講解這道簡單試題時引發學生的質疑，出乎意料，展示如下

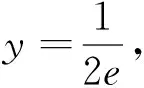
學生提的有道理，只憑x>0時，g(x)>0，在(1,+∞)單調遞減就判斷以x軸為漸近線思維有點不嚴謹.函數的極限人教A版并未涉及到.

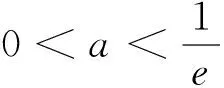
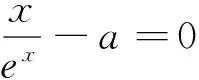
很多學生表示同感，向筆者投入期待的眼神與焦急的等待.

師：很難找，當然不能隨便找，是否可以先來研究一下找這個數應該具備哪些性質？各小組討論交流一下，我們現在的問題是討論f(x)在區間(1,+∞)上僅有一個零點存在問題.

學生C：因為a在變化，所以找到的m不能是一個定值，應該與a有關，隨著a的變化而變化.

學生D：所取的m必須在區間(1.+∞)內，而且對應的函數值必須小于a.

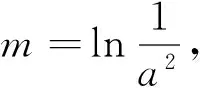
師：很好！證明思想很到位.同學們還有其他想法嗎？

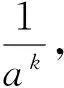
師:學生F展示了探尋過程，有道理，自然流暢，值得大家學習.

三、拓展延伸

零點區間隨參數的變化而變化，則可借助于常用結論來設計自變量的取值方向，為成功使用零點存在定理奠定基礎，與指數、對數函數有關的常用結論很多，現列舉如下：

(1)ex>x在區間(0，+∞)內恒成立；

(2)ex≥x+1在R上恒成立；

(3)ex>x2在區間(0，+∞)內恒成立；

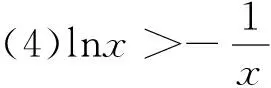
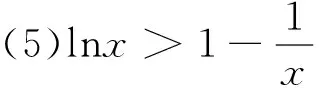
(6)lnx

(7)lnx

例題(2017年甘肅省第三次高考診斷測試第20題)已知函數f(x)=x(lnx-ax)(a∈R).(Ⅰ)當a=0時，求函數f(x)的最小值；(Ⅱ)若函數f(x)有兩個極值點x1,x2(x1

x(0,12a)12a(12a,+∞)y'+0-y單調遞增極大值y(12a)單調遞減

隨著新課改的縱橫發展，研究的逐步深入，高考試題的不斷推舊出新，給高中數學教學帶來新的挑戰與任務，教師要潛心研究設計出切實可行的操作方案，這樣才能在教學中高屋建瓴，有的放矢.