多維度延伸2017年江蘇數學高考第20題

江蘇省鎮江市丹徒高級中學 吳海軍 邱紅英

2017年的江蘇高考數學題令人矚目，尤其是第20題，被眾多老師意為“繞口令”，且具有高等數學之背景。那么我們就來探究延伸此高考神題。

真題再現：已知函數有極值，且導函數 的極值點是 的零點。

（1）求b關于a的函數關系式，并寫出定義域；

（2）證明： ；

首先我們審題，如果概念不清楚，真會搞混。題目中導函數的極值點其實就是原函數二次求導所得函數的零點，函數 有極值就是其導函數有解（拐點除外）。

題目分析完畢，我們開始探索其解答：

第一問是求函數關系式，難度在于定義域，但只需排除拐點即可，考場中很多同學就是忘記排除拐點。

令 ，得（注意：此處為導函數的極值點）

∴ 當， 的極小值為

∵題目要求 的極值點為 的零點，

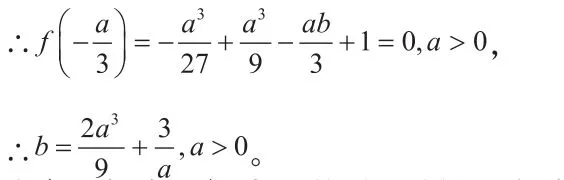
注意：相當一部分同學到此處就以為結束了，其實原函數有極值還需繼續考慮。

∵ 有極值，且

∴ 方程 有實根（拐點情況除外），

∴ 從而

當 時，故 在R上是增函數，沒有極值，舍去。（注意：導函數有解不等價于原函數有極值）

綜上，

延伸反思：其實從首問便看出此類題目的核心點便是定義域，定義域的確立往往與題目的隱含條件相掛鉤，特別是拐點，與基本不等式、方程解的有無意義相扣。

那么完全平方（立方）公式還有什么妙用呢？我們借開頭的高考題第20題第3問繼續探究下去。

第三問容易理解，只要將的極值寫出即可，并求和。

解：設 的極值點為

寫到這，靈敏的同學感覺要使用韋達定理，為什么？二次函數要想把根寫出來，再代入原函數求解，根本就是異想天開，所以遷移能力好的同學們便能寫下去。

從而

∴ f（x1）+f（x2）=（x1+x2）+2，

為何之和是0？其實此處有一個相當漂亮的三次函數的性質：

函數f（x）= ax3+bx2+cx+d的圖象是關于稱的。

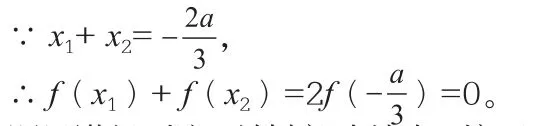
題目進行到這，關鍵部分結束，接下來只要對原函數求極值即可。

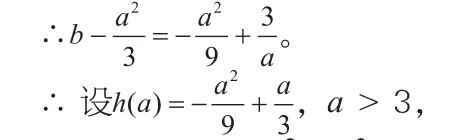
∴ 求導得函數h（a）在定義域上單調遞減。

∵ h（6）（注意：題目中的是隨便給的嗎？顯然不是）

∴ a∈ 。

往往存在某個x，使得f（x）=z，且z為題中必要常數。

壓軸之問雖解完，但這其中的代換思想、完全平方式思想我們已經體會過，下面我們探究一道與之相關的題型：

已知函數實數 滿足求8s+8t的取值范圍。

老師點評：這最后一步的求解和2017年壓軸題最后一問的方法是一樣的，此處略。這其實是多次求導問題的本質。

分析：本題主要考查初等函數的基本性質、導數的應用等知識，考查運用數學思想方法解決問題的能力。在第三問中，我們發現這個式子中含有e，且是指數式，不難想到與對數有關，再精確一點就是與ln有關，而在對數公式里有關于商的對數關系，就可以想到是作商比較！

探究到此，我們發現一道高考神題能夠衍射出如此之多技巧與背景，與如此之多題目相互滲透，說明數學學科的聯系之緊密，之博大精深，正所謂學無止境，任何人唯有在數學的海洋中不斷探索前行，方能摘得那一顆顆璀璨的珍珠。

[1]于洋，傅海倫，陳梅．對數學高考研究的再認識[J]．教學與管理（中學版），2015（4）：77-79．

[2]戴安東．2017數學高考有感[J]．新高考（高三數學），2017（9）：8．