全等三角形的判定專題復習教學

譚靜雪

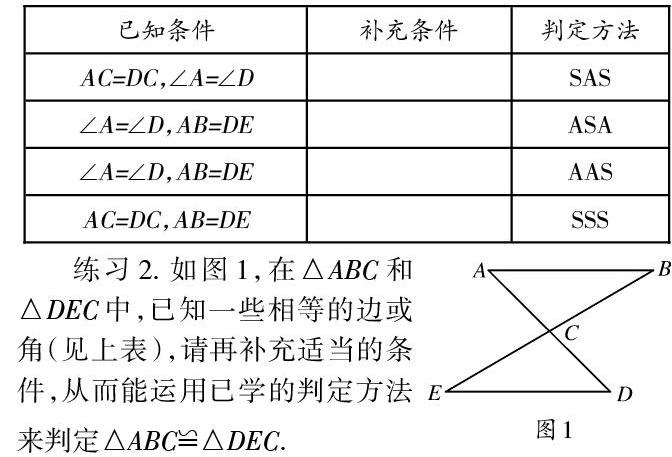
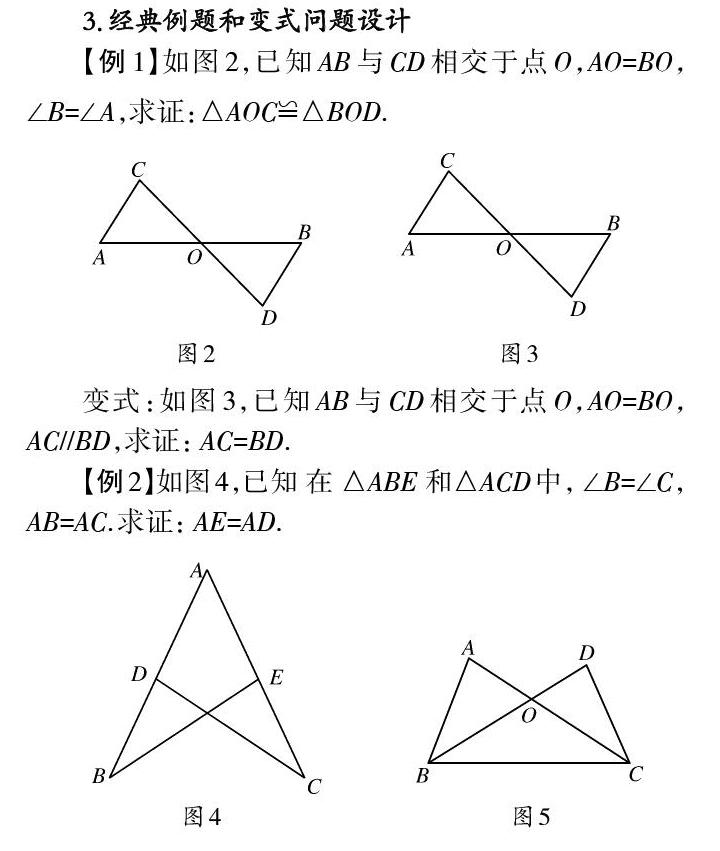
[摘 要]初中階段圖形之間最重要的關系之一就是全等，而全等三角形的判定又是引導學生學會演繹證明的重要內容.在全等三角形的判定專題復習課中引導學生回歸知識起點，總結歸納，更好地尋找解題方法，對學生之后的學習有實際意義.

[關鍵詞]全等三角形；判定；復習；初中數學

[中圖分類號] G633.6 [文獻標識碼] A [文章編號] 1674-6058（2018）17-0016-02

初中階段圖形之間最重要的關系之一就是全等，而全等三角形的判定又是引導學生學會演繹證明的重要內容.在全等三角形的判定專題復習課中，引導學生回歸知識起點，追本溯源，利用平移、旋轉、軸反射來研究三角形全等的判定，快速找到解題突破口，靈活添加輔助線解決問題，總結歸納解題方法，對學生之后的學習有實際意義.

一、教學目標

（1）理解并掌握全等三角形的判定定理；

（2）會應用判定定理進行推理判定兩個三角形全等.

二、教學重點、難點

全等三角形的判定定理；靈活應用判定定理解題；會添加輔助線證明三角形全等.

三、教學過程

【設計意圖】學生推理能力的發展是一個長期的過程，教學中充分考慮了學生的身心特點和認知水平，注重了教學要求的層次性.判定兩個三角形全等，直接可用的條件由多到少，由論證一次全等過渡到論證兩次全等，圖形由簡單到復雜，證明的結論由“全等”遞進到“邊或角等”，從不需要添加輔助線到需要添加輔助線.這樣使得推理證明層次分明，坡度平緩，更有助于學生學習綜合法證明.

【設計意圖】添加輔助線解題是本題的關鍵，如何引導學生添加輔助線則是教學的重難點.方法一利用旋轉的觀點作出輔助線DG，得到△DGF≌△ECF，從而得到DG=CE，再證明DG=AD，從而得到DG=AD=CE.方法二利用旋轉的觀點延長FC到N，使得FN=FA，得到△ADF≌△NEF，則NE=AD，再證明CE=NE，從而得到NE=CE=AD.通過兩種方法拓寬學生思路，發散學生思維，加深學生對利用旋轉的觀點構造全等三角形，打開思路突破重點、難點，從而解決問題的優越性.

綜上所述，在作輔助線的過程中，改變以往強調從三個判定條件入手找輔助線的抽象做法，引導學生回歸知識的起點，利用平移、旋轉、軸反射等方法變換得到全等三角形，讓學生在學習中弄懂知識的來龍去脈，找到作輔助線的訣竅，培養學生學習的興趣和邏輯推理能力.

（責任編輯 黃桂堅）