《18.2.1矩形》教學設計及幾點思考

☉江蘇省揚州市邗江區公道初級中學 湯恒錦

近期，筆者有幸在市級“骨干教師示范課”的聽課活動中聆聽了一節關于矩形的定義和性質的示范課，聽后受益匪淺，下面對其教學設計進行簡述，并結合評課環節和自己的理解給出兩點思考，不當之處，敬請指正.

一、教學內容

人教版初中數學八年級下冊第52頁～53頁.

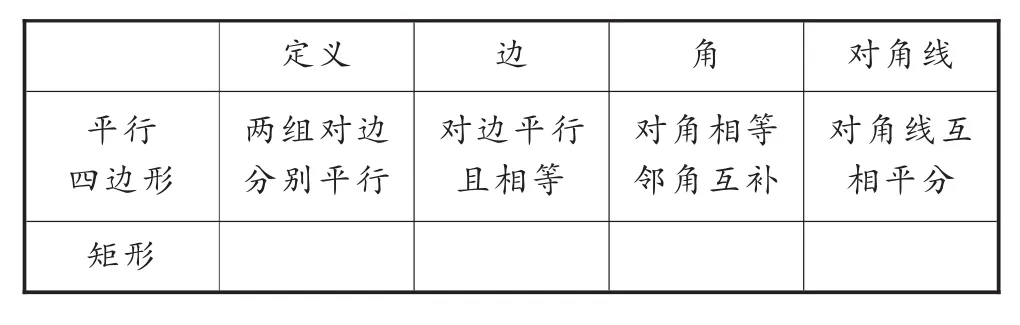
定義 邊 角 對角線平行四邊形對角線互相平分矩形兩組對邊分別平行對邊平行且相等對角相等鄰角互補

二、教學設計

（一）復習舊知，新課引入

設計意圖：開課之初，引導學生復習剛剛學習過的平行四邊形，其有三個目的：一是復習舊知；二是為學生后續研究新知（矩形）做鋪墊；三是為了引入新課，在動態圖形變化中溝通平行四邊形和矩形之間的關系.

（二）變換圖形，形成概念

概念：有一個角是直角的平行四邊形叫做矩形.

設計意圖：通過幾何畫板動態演示，引導學生自主構建矩形的定義，并明確矩形與平行四邊形之間的關系是一種特殊的平行四邊形 （同時完善上表相關內容），為學生理解“矩形具有平行四邊形的所有性質”埋下伏筆.

（三）探究性質，深化認知

問題：矩形有哪些性質？（師生交流中完成上表的所有內容）

定義 邊 角 對角線平行四邊形兩組對邊分別平行對邊平行且相等對角相等鄰角互補對角線互相平分矩形有一個角是直角的平行四邊形對邊平行且相等對角相等鄰角互補，四個角是直角？對角線互相平分且相等？

設計意圖：首先，對定義中的關鍵詞以加黑字體的形式呈現；其次，引導學生進一步明確矩形具有平行四邊形的所有性質，然后引導學生觀察圖形，猜想得到矩形所特有的性質，同時用“？”的形式結尾，使學生知道“猜想是需要證明的，并不是所有的猜想都正確”.

（四）演繹推理，形成定理

性質定理1：矩形的四個角都是直角.

設計意圖：由學生自主完成，較簡單，主要運用了平行四邊形的性質和四邊形的內角和的度數.

性質定理2：矩形的對角線相等.

設計意圖：教師講解并板書，此處需要使學生明確如何證明線段相等？即需要通過構造全等三角形進行證明（如圖1和圖2），引導學生初步體會可以通過三角形的性質來研究矩形所具有的性質.同時，完善性質定理1和性質定理2的文字語言、圖形語言和符號語言.

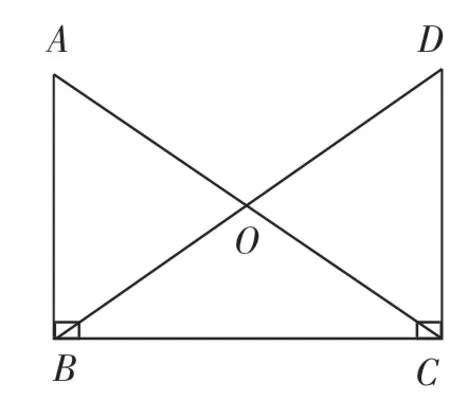
圖1

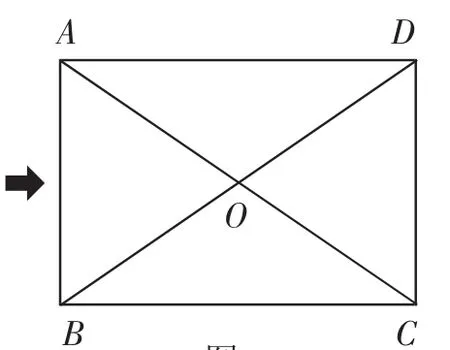
圖2

（五）知識應用，解決問題

例1 如圖2，矩形ABCD的對角線AC、BD相交于點O，∠AOB=60°，AB=4cm.

（1）求矩形對角線的長；

（2）求矩形周長.

設計意圖：鞏固性質定理1和性質定理2，同時引導學生進一步體會矩形問題通常轉化為直角三角形或等腰三角形來解決.

（六）觀察分析，定理探究

如圖3，矩形ABCD的對角線AC、BD相交于點O，請討論OC與BD的關系.

設計意圖：在前述鋪墊的基礎上，通過矩形的性質，得到直角三角形中非常重要的一個性質（如圖4，課件動態演示圖3到圖4的變化過程）：直角三角形斜邊上的中線等于斜邊的一半.同時給出該性質定理的三種語言：文字語言、圖形語言、符號語言.

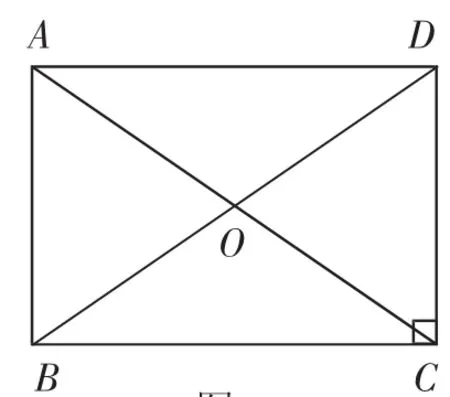
圖3

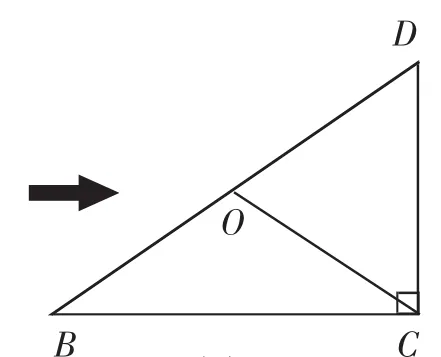
圖4

（七）強化記憶，熟能生巧

例2 已知三角形ABC是直角三角形，∠ABC=90°，BD是斜邊AC上的中線（圖略）.

（1）若BD=3，則AC=_____；

（2）若∠C=30°，AB=5，則AC=_____，BD=_____，∠BOC=_____.

設計意圖：鞏固所學，同時復習直角三角形中30°的角所具有的性質.

附1：教學目標

（1）理解矩形的概念，明確矩形與平行四邊形的區別與聯系；

（2）探索并證明矩形的性質，會用矩形的性質解決相關問題；

（3）理解“直角三角形斜邊上的中線等于斜邊的一半”這一重要結論.

附2：課堂小結（圖5）

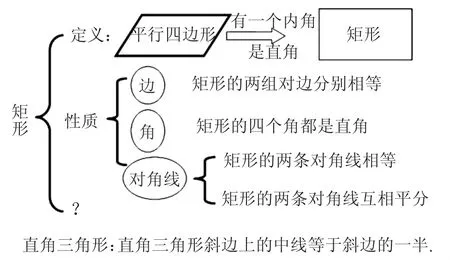
圖5

設計意圖：在新課結束時引導學生再次對照學習目標反思自己的所學；以框圖的形式引導學生系統梳理本節課所學的知識，為學生構建完整的知識網略，同時引導學生做好課下復習和預習工作（圖5中的問號）.

附3：達標檢測和課后作業（略）.

三、兩點思考

（一）幾何圖形研究“套路化”

人民教育出版社資深編審章建躍博士指出：“要重視‘基本套路’的教學.”本課例設計過程中始終貫徹幾何圖形研究的基本套路：定義、性質、判定，而且定義和性質的判定都是從邊、角、對角線給出的，這為學生后續研究相關基本圖形打下了堅實的基礎.

此外，本課例也為后續定理的學習做好了鋪墊，形成了定理學習的基本方法：觀察圖形、發現猜想、證明猜想，形成定理等.這種教學方法在培育學生形成理性思維（中國學生發展核心素養之一）和邏輯推理（數學學科核心素養之一）能力方面進行了很好的嘗試，而且取得了不錯的課堂教學效果.

（二）例題習題設置“序列化”

在評課環節，各位老師認為本課例另外一個最大的亮點在于例題和習題設置的序列化，比如第1題從教材例題出發，又追問了矩形的周長；第2題則很好的鞏固了直角三角形的性質定理和30°的角所具有的性質，很好的將直角三角形中兩個常考的知識點進行了融合，實現了一箭雙雕的效果.

此外，該課例還具備前后照應（引入和結尾）和承前啟后（圖5中的“？”）的典型特點，值得其他教師學習和借鑒.

四、結語

教學設計中的設計意圖是筆者根據聽課感受和自己的理解所添加的，最后的兩點思考融合了參與評課教師的集體智慧.然而，對優化課堂教學的追求永無止境，也是仁者見仁、智者見者的，不當之處，敬請指正.