對話教學：構建數學課堂的新樣態

江蘇南京市寶船小學（210036）

對話教學，指在教學過程中師生雙方圍繞共同的學習主題，通過積極的、富有創意的交流互動，不斷發現和探索教學中存在的問題，實現對問題的解決和知識的建構的過程。弗萊雷提出：“沒有了對話，就沒有交流，沒有了交流，也就沒有真正的教育。”

對話教學，積極尋求重建數學課堂文化的路徑，營造良好的數學課堂文化氛圍，創造充滿生命力的學習樂園。

對話教學把課堂看作是促進生命發展的生態系統。數學學習內容、媒介信息、情感態度等，都在這個系統中外顯為師生對話、生生對話、生本（文本）對話、自我對話，一起討論、交流、碰撞、激勵、共享……

一、創設情境，讓學生樂于表達

在對話課堂里，教師和學生的角色定位發生了變化，教師從知識的傳授者向學習的組織者轉變；學生不只是接受者，還是學習的設計者和參與者，二者的角色在“學習共同體”的動態平衡中實現轉換。對此，教師要善于給學生創設有效的問題情境，激發學生的探究欲望，鼓勵學生自主探索和合作交流，讓課堂成為充盈信任、愉悅和智慧的樂園。

例如，教學“認識一個整體的幾分之一”時，教師創設了這樣的情境：

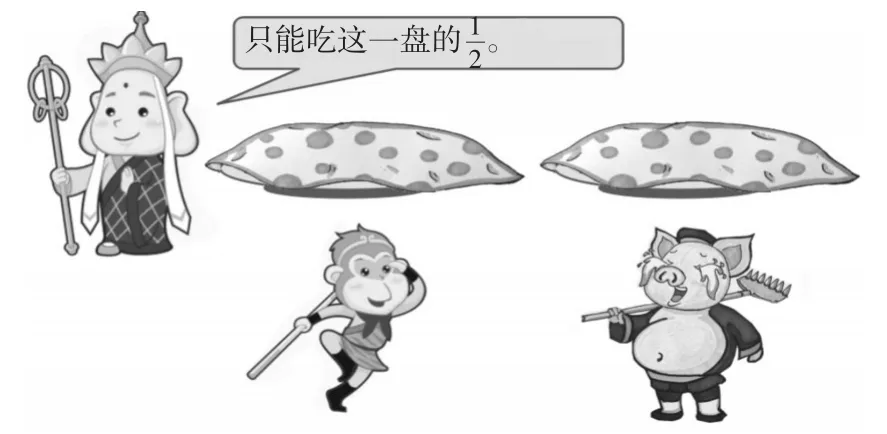
圖1

師（出示圖1）：唐僧拿出兩盤桃，請孫悟空和豬八戒吃，并要求只能吃每盤桃的1/2。兩個徒兒迫不及待地各搶了一盤，可是打開一看，豬八戒卻哇哇大哭起來。想一想，這是為什么呢？

生1：可能兩盤桃的個數不一樣。

生2：可能孫悟空的那盤桃很多，豬八戒的那盤桃卻很少。

（很多學生表示贊同）

師：很有想法。你能用小圓圈來表示桃，用虛線分一分，找到這盤桃的1/2嗎？

（學生活動，很快有人舉手）

生3（上臺展示自己的分法）：我用10個圓圈表示孫悟空的那盤桃，它的1/2有5個；用2個圓圈表示豬八戒的那盤桃，它的1/2只有1個。豬八戒的太少了，所以他才會哭。

生4：我用8個圓圈表示孫悟空的那盤桃，它的1/2有4個；用4個圓圈表示豬八戒的那盤桃，它的1/2有2個。

師（指著其中的一盤桃）：能說說你是怎樣找到這盤桃的1/2的嗎？

生5：只要把8個桃平均分成兩份，其中的一份就是1/2。

師（指著另一盤桃）：為什么從4個桃里也能找到1/2？

生6：因為把4個桃平均分成兩份，其中的一份就是1/2。

生7：不管盤子里有幾個桃，只要平均分成兩份，就能找到它的1/2。

生8：無論桃有多少，找到了一半就能找到1/2。

師：很有見解！我們可以把一盤桃看作一個整體（畫圈），平均分成兩份，每份就是它的1/2。

上述教學中，學生在無法清晰表達“兩盤桃到底有何不同？”時，教師創設了生動有趣的“分桃子”的情境，借助“畫一畫”“分一分”“比一比”等活動，引導學生展開生生對話、自我對話，而教師恰當的追問、反問，能引領學生逐步觸及知識的本質——“部分與整體的關系”，加深對“分數具有無量綱性”這一本質的理解。

二、多維互動，讓學生自主探究

曹培英老師認為：學科核心素養不是針對學科專業人才的特殊需要，而是適用于普遍情景和所有人的共同素養。課堂學習的多維互動有利于學生思維品質的拓展和提升，而對于不同的學習素材和數學問題，不同的學生也會有不同的理解，這為課堂開展對話教學奠定了基礎和提供了契機，也為學生核心素養的培養提供了生長的“土壤”。

例如，在教學“認識小數”時，教師組織學生進行如下實驗探究。

師（出示圖2）：下面的每個圖形都表示1角，你能在圖中表示出0.1角嗎？在學習單上試一試。

圖2

（學生獨立思考，自主完成）

生1（上臺展示）：我選擇的是線段，在左邊畫一段，就是0.1角。

生2：不準確。隨便畫一段，不一定是0.1角，應該把線段平均分成10份，其中的1份才是0.1角。

師：很嚴謹，畫圖就應該準確。還有不同的想法嗎？生3：我把長方形平均分成10份，其中的1份是0.1角。生4：把正方形平均分成10份，其中的1份也是0.1角。師：為什么一定要平均分成10份呢？

生4：1角等于10分，平均分成10份，1份就是1分，也就是0.1角。

師：這種平均分的方法，還可能得到什么數呢？生5：1/10。

上述教學中，充分利用學生已有的認知經驗，引導學生根據“分一分”“涂一涂”直觀圖來研究小數的意義，適時展開師生、生生對話，可使“小數”從具體的量中抽象出來，從而使數學建模的過程更具深度，也為學生初步理解“小數實質上是十進分數的另一種形式”提供經驗支持，能讓學生真正體驗到小數的產生是生活和生產的需要。給學生提供豐富的數學活動材料，引導學生經歷探索的過程，不但能為學生創設合理想象、自由思維的空間，把學生帶到從未知走向已知的“高速”通道，還能使知識在教學層面實現“軟著陸”，往往會有“意外”的收獲。

三、因勢利導，讓學生主動思辨

對話是課堂建設者之間一種共生的交往關系，意味著對話主體間的相互理解、視界融合及經驗分享。引導學生主動思辨，經歷核心知識的形成過程，并且讓學生正確理解核心知識，學會“用數學的語言表達世界”，就有可能讓學生逐步養成數學的理性思維。

例如，教學“表面積的變化”時，教師設疑并組織學生討論。

師（出示圖3）：如果從棱長為3 cm的正方體上挖去一個棱長為1 cm的小正體，它的表面積會發生變化？

生1（很快舉手）：挖去一部分，大正方體的表面積當然會變化。

師：你能說說它的表面積是怎么變化的嗎？

生1（遲疑）：應該會變小吧。

生2（很快反駁）：不一定會變小，也有可能不變。

師：你能具體說一說嗎？

生2：如果從頂點處挖，大正方體的表面積應該是不變的。

師：對于這個問題，你們還有什么新的想法？

（學生猜想、操作、驗證結論）

生3：從一個頂點處挖去3個小面，但又露出了3個小面，大正方體的表面積確實不變。

生4：從一條棱的兩邊各挖去1個小面，但又露出4個小面，大正方體的表面積反而增加了。

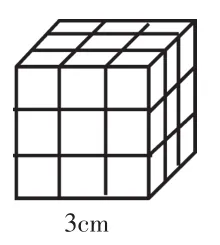
圖3

生5：從一個面的中間挖去1個小面，但露出了5個小面，大正方體的表面積增加了4個小面。

師：采取的方法不同，大正方體的表面積的變化也不同。

以核心問題為載體、學生自主參與為主線的學習活動，更需要適時展開師生、生生對話。一方面，可以促使學生深入了解學習素材，從整體上建立對數學知識的初步感知；另一方面，還能指向學生的最近發展區，優化學生的思考方式，引發學生新的思考和感悟，實現深度學習。

四、長效提升，讓學生合作共贏

數學課堂的教學設計要有“教育的格局”，不囿于一題、一課，而應著眼于學生的生命成長，體現知識、能力、情感培養的整體性。課堂不能流于單一的“問答式”，而應通過交流、爭辯、質疑、分享等方式，實現教學主體之間的多維度對話，從而建構一個以知識、能力、人格為基礎，以數學素養、生命成長為頂層的學習空間。

例如，教學“用數對確定位置”的結課階段，教師組織學生討論。

師：剛才我們學習了用數對確定位置。那么你覺得確定一個點的位置，需要幾個數呢？

生1：2個數。

師：如果只用一個數，行嗎？

生1：肯定不行。

師：為什么？（出示圖4）誰能說說在0和2中間的這個點可以怎樣表示？

圖4

生2：可以用“1”表示。

師：你看，剛才的這個點，不就是只用了一個數就確定位置了嗎？那么，“3”的位置在哪呢？

生3：在2的后邊。

師（笑）：還是只用一個數就確定了它的位置。

生3（反應過來）：情況不一樣。這里只有一行，確定點的位置，當然只需要一個數了。

生4：今天學的不只是一行或一列，而是好幾行好幾列。需要先確定它在第幾列，再確定它在第幾行，所以要用到兩個數。

師：真會思考！這樣看來，確定位置有可能用一個數，有可能用兩個數，那么——

生5：還有可能用到三個數。

師：確定位置時，究竟會不會用到三個數呢？這個有趣的問題，留給同學們課后研究。

綜上，對話為學生創設了“伸出窗外”的空間，為學生的數學思維走向更深層次提供了無限可能。實施多樣的對話，引領數學學習從經驗走向理性，讓學生真正“學得到”“帶得走”，是數學生態課堂發展的必然訴求，是對發展核心素養的積極回應。