“認識三角形”教學實踐與思考

江蘇省海門實驗學校附屬小學 沈 儉

【片段一】

導入：同學們看，這是我們美麗的校園，咱們一起來欣賞（播放一組圖片）。

師：一起來看這幾幅圖片，這些圖片里都藏著一個我們熟悉的圖形，是誰呢？

生：三角形！

師：（課件閃動三角形）認識三角形嗎？

生：認識。

師：今天這節課，我們一起帶著數學的眼光來進一步認識三角形。

師：（從圖片中抽象出三角形）你們能自己動手做一個三角形嗎？老師給大家提供了一些材料（小棒、釘子板），你可以選擇一種材料做出一個三角形，也可以畫一個三角形，然后同桌互相展示，并思考：三角形有什么特點？

展示交流：

生1：我是用釘子板圍了一個三角形。

師：誰也是用釘子板圍的？

（體會：同樣是用釘子板圍成了三角形，但他們圍出的樣子是不一樣的）

生2：我用小棒擺的（在實物投影儀上小心翼翼地擺著，看似簡單的操作，可是一不小心小棒與小棒之間就不相連了）。

師連忙追問：擺的時候要注意些什么呀？

（體會：一定要做到“首尾相接”）

生3：我是畫了一個三角形（在黑板上畫）。

引導觀察：不管是圍成的三角形還是畫出的三角形，都有什么共同的特點呢？

揭示：三條線段首尾相接圍成的圖形叫作三角形。

【思考】

我們都知道，學生并非一張白紙。生活中處處有數學，日常所見使他們或多或少地對所要學習的數學知識有所了解。因此，從熟悉的校園場景引入，自然地提出了學習內容，感覺到三角形就在身邊，更是感受到了數學是那么親近的。然而，數學學習有時特別需要強調嚴謹性，對于“三條線段首尾相接圍成的圖形叫作三角形”這一概念的建立，深刻認識“首尾相接”至關重要，因此教學中設計了“動手做三角形”，通過圍一圍、擺一擺或畫一畫引導學生加深體驗，課堂上尤其是抓住了一個細節——用小棒擺三角形時，看似簡單的操作，卻需非常小心才得以成功，實現了對三角形核心概念的歸納與梳理。

【片段二】

引導：在一張紙上（呈現方格紙）任意畫3個點，以這3個點作為頂點一定可以連成一個三角形。這句話對嗎？

學生借助方格紙動手操作，然后同桌討論后指名發表意見。

借助課件進一步演示，引導學生思考、判斷。共同得出：三個點的位置不在同一條直線上，就能圍成不同的三角形；當這3個點在一條直線上時，就不能連成三角形。

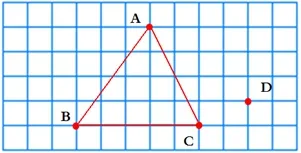
引導學生繼續挑戰，出示研究單：下面的方格紙上有4個點，從這4個點中任選3個作為頂點畫一個三角形，一共可以畫幾個三角形？

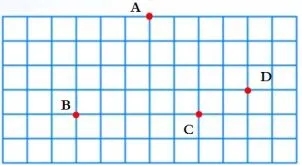
研究要求：先獨立思考，再和同桌說一說：可以選擇______、、______ 、______ 三個點作為頂點畫出三角形，一共畫______ 個。

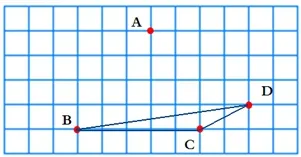
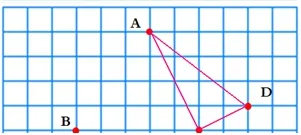
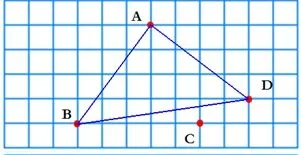
集體交流時，引導學生可以如下圖這樣有序思考：A不選，可以連成一個三角形；B不選，也可以連成一個三角形……只要三個點不在同一條直線上都可以連成三角形。

【思考】

動手操作，親歷研究，在主動建立數學認識的過程中是不可或缺的。教材中的“試一試”是讓學生明確“三角形的三個頂點不能在同一條直線上”，這一知識在成人眼里也許是簡單的，但簡單的背后往往蘊藏著豐富。教學中設計了以上兩個層次的探究活動，每一次都為學生提供了研究材料——方格紙，兩次的研究遵循了由淺入深的過程。研究過程中，觀察到了學生能自覺地畫一畫、連一連、說一說，為有效的交流展示提供了支撐。同時，教師適時的方法指導有利于思維的發展。

【片段三】

師：通過剛才的學習，咱們知道了什么是三角形的高，一起來讀一讀：從三角形的一個頂點到對邊的垂直線段是三角形的高。

師：這句話不僅說清了什么是三角形的高，其實還說明了怎么畫高。再讀讀，體會一下，怎么畫高。

學生動手試一試畫出三角形底邊上的高，畫完后和同桌交流一下自己的畫法。教師收集學生作品，準備集體展示。

展示1：這條高畫對了嗎？如何去檢驗畫得對不對？并提醒：畫高一般用虛線畫，注意標上直角標記。

展示2：（呈現的是一份錯例）這個呢？誰來給它檢驗、評價一下？

教師進一步指導點撥：看來，想把高畫好確實有一定的難度，老師有一個畫高的法寶，想看一看嗎？借助課件演示并總結畫高的方法：（1）找準頂點和底邊；（2）直角邊對齊底和點；（3）畫高一般用虛線；（4）直角符號要標上。

這就是畫三角形高的步驟，現在都學會了嗎？那我們再來畫一畫，同桌檢查。

師：還是看這個三角形，已經畫了一條高，還能畫出高嗎？能畫幾條呢？

生：能畫3條。

師：為什么能畫3條？

生：因為頂點到對邊有三組。（學生獨立畫出另外兩條高）

師：看看這個三角形的三條高，你有什么發現？

生：這三條高相交于一點。

師：讓我們繼續往下探索，看看還能發現什么秘密。還是看這個三角形（加上方格紙），它的底是幾厘米？高是幾厘米？

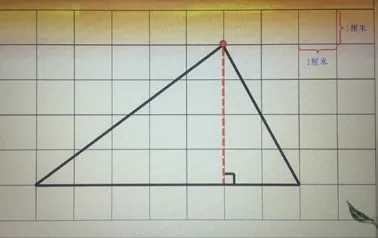
師：我們把它變一變（上面的頂點往左移動），現在誰來找出新的三角形的高？

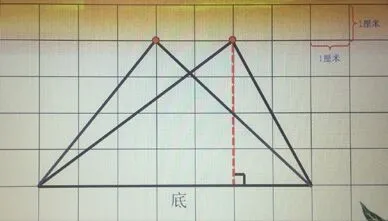
繼續變，學生依次找出相應三角形的高。

師：仔細觀察，又能發現什么？

生：三角形的一個頂點雖然往左移了，但它們的高是相等的。

師：還能畫出以它為底，高是4厘米的三角形嗎？ 能畫多少個？

生：還能畫，而且能畫無數個。

師：那就繼續看，再往左移，現在是個直角三角形了，這條底邊上的高在哪兒呢？

集體討論后指出：這個三角形比較特殊，兩條直角邊本來就是互相垂直的，所以它的兩條直角邊互為底和高。

引導觀察課件，繼續變一變，出現鈍角三角形了，現在這條底邊上的高怎么畫？

師：看來，有的高在三角形里面，有的高正好和三角形的邊重合，而有的則在三角形的外面。關于三角形的高，秘密還真不少。看來，探索的道路還真是永無止境啊！

【思考】

圍繞“三角形的高”設計了豐富的活動，讓學生充分感悟“高的秘密”。教材提供的例子是畫銳角三角形的高，對于直角三角形的高放在練習題中呈現，對于鈍角三角形外部的高則沒有提及，所以多數教師也只停留在教例題、做習題的層面。但是有些數學知識是有著聯系的整體，如果當學生明白了銳角三角形、直角三角形有三條高，一定會自然而然地想找鈍角三角形的三條高在哪兒。所以以上教學環節中，充分挖掘知識的“深化點”，在同一問題情境中將三角形的高有效整合，通過不斷地追問引領學生觀察和思考，經歷同底、等高的三角形的變化中使學習得到適當的延伸，使認知結構得到不斷完善。