立足教材 活用教材
——“一元二次方程”教學設計及立意闡釋

☉江蘇省建湖縣建陽中學 譚萬祝

近期，筆者有幸參加了所在地區(qū)初中數(shù)學“一人一課”活動，并取得了優(yōu)異成績.執(zhí)教課題是“一元二次方程”.下面對其教學設計進行簡單介紹，并給出一些初步思考，不當之處，敬請指正.

一、教學內(nèi)容

第1頁至第4頁.

二、教學流程

1.知識回顧，情境引入

在復習一元一次方程相關知識的基礎上，呈現(xiàn)教材第1頁章前圖、章引言及第2頁問題1，并引導學生在明晰題意的基礎上列出方程.

2.觀察思考，得出定義

章前圖、章引言 問題1

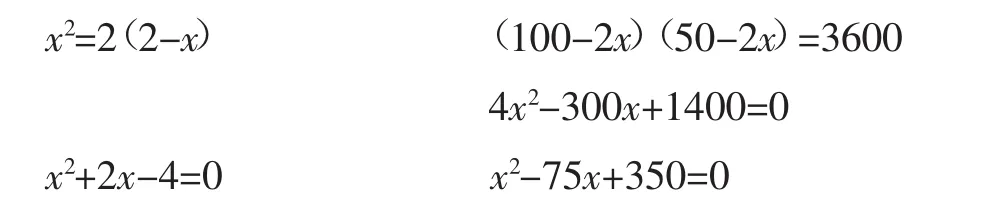
思考：（1）它們是一元一次方程嗎？

（2）類比一元一次方程，你能給它們命名嗎？能說出它們的主要特點嗎？

圖2

3.自主練習，微課助學

練習1：（1）你能舉出一個一元二次方程的例子嗎？

（2）你能舉出一個不是一元二次方程的例子嗎？為什么？

練習2：判斷下列各方程是不是一元二次方程.如果不是，請說明理由.

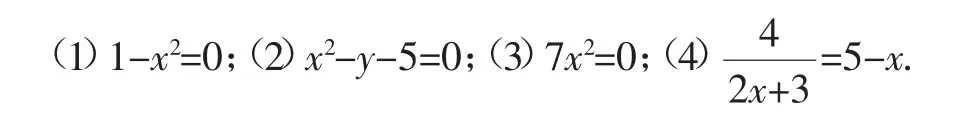
在完成練習1和練習2的基礎上，播放微課：“一元二次方程”自述（PPT及微課文本如下所示）.

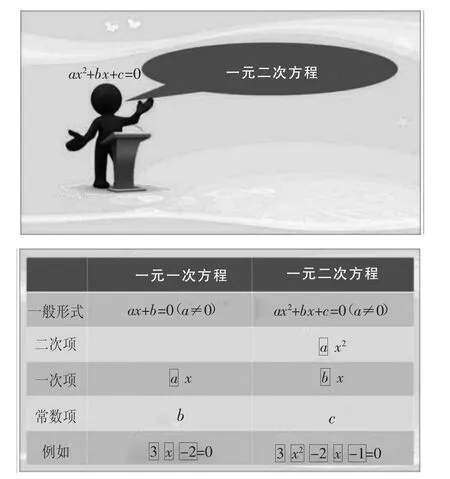
圖3

同學們，大家好，我叫“一元二次方程”，是你們這節(jié)課剛剛認識的新朋友，你們可能和我還不太熟悉，但我相信你們肯定和我的孿生兄弟“一元一次方程”是好朋友，它的樣子如下：ax+b=0，其中a≠0，我們把ax稱為一次項，a叫作一次項的系數(shù)，b稱為常數(shù)項，比如3x-2=0的一次項是3x，一次項系數(shù)和常數(shù)項分別為3和-2.

我的樣子如下：ax2+bx+c=0，其中a≠0，我們把ax2稱為二次項，bx稱為一次項，a、b分別叫作二次項和一次項的系數(shù)，而c稱為常數(shù)項，比如3x2-2x-1=0的二次項、一次項、常數(shù)項分別為3x2、-2x、-1，而二次項系數(shù)和一次項系數(shù)分別為3和-2.

同學們，以后的日子我們慢慢相處吧，相信我們一定也會成為好朋友的.

4.鞏固新知，典例分析

圖4

典例分析：

呈現(xiàn)教材第3頁例題.

練習3：將下列方程化為一元二次方程的一般形式，并寫出其中的二次項系數(shù)、一次項系數(shù)和常數(shù)項.

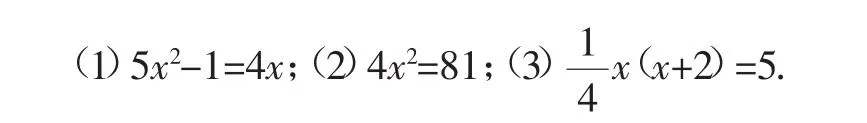
練習4：教材第2頁問題2.

呈現(xiàn)教材第2頁問題2，并得到方程：x2-x=56，然后列表（如表1）：

表1

通過親自動手填寫表1，很容易發(fā)現(xiàn)：當x=8時，x2-x=56；也很容易“喚醒”學生以前對方程的“根”的認識，進而可以很容易得到一元二次方程的“根”的概念.通過驗證，我們發(fā)現(xiàn)：當x=-7時，x2-x=56也成立，這說明如果不考慮實際問題，x=-7也是方程x2-x=56的一個根.

此時出示本節(jié)課的學習目標：

（1）理解一元一次方程的概念是以未知數(shù)的個數(shù)和次數(shù)為標準的；

（2）掌握一元二次方程的一般形式及三種特殊形式，能將一元二次方程化成一般形式；

（3）理解一元二次方程根的概念，會判斷一個數(shù)是否是一個一元二次方程的根.

5.達標檢測，作業(yè)設計

達標檢測：（1）下列方程是關于x的一元二次方程的是____（填序號）.

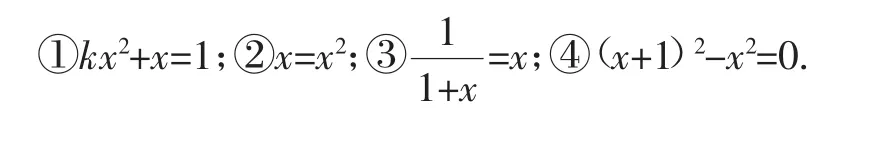
（2）將關于x的一元二次方程（x+1）（x-3）=2（x-1）2化成一般形式，并指出二次項系數(shù)、一次項系數(shù)和常數(shù)項.

（3）m為方程x2+x-6=0的一個根，則代數(shù)式m2+m的值等于______.

作業(yè)設計：

必做題：（1）P4復習鞏固1、2、3；（2）每人寫一篇數(shù)學日記《一元二次方程自述》.

選做題：P4復習鞏固6、7.

三、教學立意

1.貫徹“基本套路”

人民教育出版社資深編審章建躍博士曾指出：課堂教學要重視“基本套路”的教學.筆者認為，關于方程教學的“基本套路”就是：實際問題、定義（一般形式、根）、解方程、應用.因此，在本節(jié)課的教學之初，筆者就以框圖的形式為學生呈現(xiàn)了一元一次方程的基本框架，在教學過程中漸次生成了一元二次方程的基本框架，為學生構建前后連貫、邏輯一致的知識體系進行了一定的嘗試，且取得了較好的教學效果.

2.踐行“用教材教”

筆者聽過多次這節(jié)課的公開課，其中有很多教師直接類比一元一次方程的概念得到一元二次方程的概念，然后進行大量的練習，正所謂“一個定義+三項注意”，評課環(huán)節(jié)有的老師還說這是“用教材教”，關于這一點筆者持反對意見.上述做法其實違背了教材的編寫意圖，沒有實現(xiàn)和教材的真正“對話”.現(xiàn)行人教版教材涉及方程（包括函數(shù)）等章節(jié)的內(nèi)容都是以大量實際問題的形式引入新課，這樣做一是為了引導學生體會數(shù)學來源于生活，二是為了將學生“列方程解決實際問題”的難點分解到每一個課時中去，而不是集中呈現(xiàn)，顯然一開始提到的做法與這種理念是背道而馳的.因此，筆者在教學中直接應用了教材章前圖（章引言）和問題1，并對問題2進行加工得到了一元二次方程根的概念，實現(xiàn)了課堂教學的預期效果.