追根溯源 直擊本質
——一道中考題的典型錯解及教學思考

☉福建省廈門市海滄中學 藍文英

解題反思不僅關系到學生對題目的理解、對數學知識和技能的應用，更關系到數學思想方法的體會與領悟，以及數學學習方法的建立和學生思維的拓展.本文由一道中考題的錯解出發，深入挖掘錯題背后的原因，追根溯源探究問題本質，談一談解題教學思考.

一、試題呈現

（2018年福建中考數學卷第23題）如圖1，在足夠大的空地上有一段長為a米的舊墻MN，某人利用舊墻和木欄圍成一個矩形菜園ABCD，其中AD≤MN.已知矩形菜園的一邊靠墻，另三邊一共用了100米木欄.

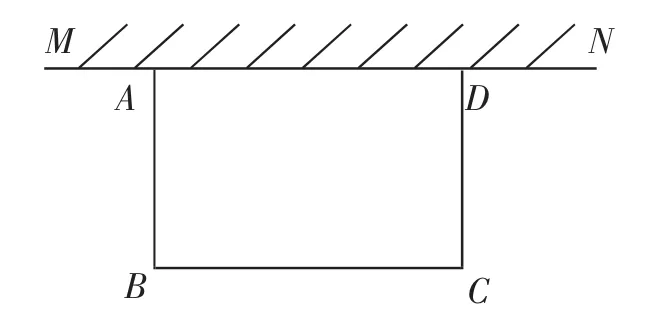
圖1

（1）若a=20，所圍成的矩形菜園的面積為450平方米，求所利用舊墻AD的長.

（2）求矩形菜園ABCD面積的最大值.

本題滿分10分，全市學生平均分不到5分，得分率偏低.筆者有幸參加中考閱卷，注意到典型錯誤主要集中為以下四類.

二、典型錯誤

1.走馬觀花，審題不清

錯解1：（1）當a=20時，由于矩形對邊相等，則AD=BC=20.

（2）設AD=x米，則0＜x≤20.

分析：錯解1和錯解2屬于典型的閱讀題目不認真，錯解1把舊墻MN的長看成矩形菜園的邊AD的長，錯解2誤認為矩形菜園四邊都是由100米長的木欄圍成.錯解3解題思路正確，離標準答案一步之遙，即沒有檢驗一元二次方程的根是否符合實際問題的意義，僅僅考慮數學問題而忽略問題背景.錯解4第（1）問成功解決，第（2）問x的取值范圍出錯，未能弄清楚第（1）、（2）問屬于兩個獨立的問題，雜糅在一塊.除此之外，對二次函數的增減性理解不深刻，錯認為函數值隨著自變量的增大而增大.從以上解答不難發現：學生審題不認真、走馬觀花，閱讀理解能力弱，缺乏對題意的推敲，對關鍵語句 “其中AD≤MN，已知矩形菜園的一邊靠墻，另三邊一共用了100米木欄”沒能好好利用就倉促解題.

2.運算能力弱，基本功不扎實

錯解5：（1）設AB=x米，則AD=BC=100-2x，則x（100-2x）=450.則100x-2x2=450，即2x2-100x-450=0.則x2-50x-225=0.利用求根公式解得（負的舍去），則AB=25+米，則舊墻AD=100-2（25+5=50-米）.

錯解6：（1）設AB=x米，則AD=BC=100-2x，則x（100-2x）=450.則100x-2x2=450，即2x2-100x-450=0.則x2-50x-225=0，根據求根公式有

我是來至中國石油工程建設公司的葉樺，畢業后一直從事EPC 工程的設計和咨詢工作。眾所周知，任何涉及到石油天然氣行業的工程都是一項龐大而系統的工作，不可能由一個人或者幾個人完成，其中涉及到繁多的工作界面劃分與專業分工劃分。因此，在設計工作中不僅要處理好技術性文件和圖紙等，還會涉及到很多溝通，協調，統籌安排的工作。

分析：錯解5和錯解6中，學生基本能正確解讀題意，解題方向明確，可是由于計算能力欠缺，導致結果出錯.錯解5錯在解一元二次方程時，移項后忘記變號.錯解6不僅移項后忘記變號，而且在求根的判別式時，方程x2-50x-225=0的常數項-225漏掉負號，錯上加錯.上述解答興許是學生馬虎導致，但不是個例，具有典型的代表性，恰巧說明學生運算能力不過關，對算理、算法理解不透徹.

3.思維不嚴謹，條理不清晰

錯解7：（2）當矩形為正方形時面積最大.

錯解8：（2）設AD=x米，則0＜x≤a.矩形菜園ABCD的面積1250，當x=50時，S取得最大值.

錯解9：（2）設AD=x米，則0＜x≤a.矩形菜園ABCD的面積則當x=a時，S取得最大值.

錯解10：（2）設AB=x米，則AD=BC=（100-2x）米.矩形菜園ABCD的面積為S=x（100-2x）=100x-2x2=-2x2+100x=-2［（x-25）2-625］=-2（x-25）2+1250.則當x=25時，S取得最大值.

錯解11：設AB=x米，則AD=BC=（100-2x）米.又AD≤MN且MN=a，則100-2x≤a，即x≥

矩形菜園ABCD的面積S=x（100-2x）=100x-2x2=-2［（x-25）2-625］=-2（x-25）2+1250.則當x=25時，S取得最大值.

4.解題不規范，書寫不當

錯解12：（1）設AB=x米，則AD=100-2x，則x（100-2x）=450，則x=45，則AD=10米.

解法13：（2）因為菜園是矩形，所以矩形的對邊相等，四個角都是直角.所以有對邊AB=DC，AD=BC.設AB=x米，則AD=BC=（100-2x）米.又AD≤MN且MN=a，則100-2x≤a，則-2x≤a-100，則，即x≥.矩形菜園ABCD的面積等于長乘寬，長為AD，寬為AB，所以面積S=x（100-2x）=100x-2x2=-2x2+100x=-2（x2-50x）=-2（x2-50x+252-625）=-2［（x-25）2-625］=-2（x-25）2+1250.則當x=25時，S取得最大值.

分析：錯解12的解答過程過于簡單，跳步多；解法13卻過于煩瑣.可以看出在日常解題教學中，有一部分學生忽略解題步驟的重要性，欠缺該方面的訓練和指導.另一部分學生則分不清楚何為必不可缺的解題步驟，無論是否必要，通通一股腦往答題紙上寫.可見，教師在平常的教學中，對學生板書的示范指導甚為重要.

三、幾點思考

本題屬于典型的“舊瓶裝新酒”問題，學生初看題目有似曾相識之感，頗為熟悉，但是要解答準確卻需扎實的基本功.從以上13種錯解典型不難發現，學生解題技能欠缺，解題反思不夠，無法對一類題型觸類旁通.此外，沒有形成完整的解題步驟和思路，缺乏審題意識、計算能力弱、邏輯思維不嚴謹等，針對此問題提出以下兩點思考.

1.關注解題反思，在學中思，在思中學

該題在本卷中屬于中等偏上難度的題，具有一定的思維含量和區分度.學生看到題目覺得熟悉，讀完題目又覺得似懂非懂，導致思維混亂，漏洞百出，究其原因，有以下幾點：審題不清楚、思考不深入、計算不扎實、解題不規范.因此，教師在平時解題教學中需引導學生多反思，反思錯因，反思數學思想方法與技能.訓練學生的審題能力和閱讀技巧，可以逐字逐句閱讀題目，一遍不夠審三遍，同時用筆圈起關鍵條件，甚至可以記錄在稿紙上.可以按照三問法步驟執行“知什么，做什么，怎么做”，梳理清楚題目條件和結構，把實際問題數學化，從而形成一套屬于自己的審題方法.

追根溯源反思解題過程中數學問題的本質，做到聞一知十.比如，本題實質是考查一元二次方程的解法、二次函數的最值問題，并且在解答的過程中考查學生的運算能力、推理能力、應用意識、創新意識，以及其中蘊含的數形結合和分類討論思想.所以在實際教學中，要注意鍛煉學生的數學思維，適當拓展高階思維.同時注重對基本概念、基本模型的滲透，無論數學問題以何種形式出現，學生都能做到有的放矢，觸及本質.

教學中要多給學生計算的時間，計算失誤不能每次都歸根于粗心，運算能力高低與否除了加強訓練，還要全方位滲透算法、算理.教師多強調、多提醒，幫助學生養成檢驗計算結果的好習慣.對以生活情景為背景的數學問題，還要考慮自變量的取值范圍是否符合實際意義，時刻不忘數學來源于生活、服務于生活的基本宗旨.

此外，優化解題方式、規范解題步驟也離不開教師的引導和示范.數學題的解答過程，不僅要條理清晰，而且要有理有據.數學語言要簡練而言之有物，切不可煩瑣冗長.教師講解例、習題時，要善于進行板書示范，在學生板演過程中全班共同探討何為不可或缺的步驟，何為可以省略的步驟，讓書寫真正做到整潔、精練，具有美感.

2.吃透教材例、習題，化舊為新，活學活用

中考題大多數為新命制的原創題，母題來源往往是教材例題或習題.以本題為例，可在人教版九年級上冊二次函數這章找到它的原型.因此，教師要重視對教材典型例題、習題的開發、研究和拓展.把例題、習題作為中考復習的第一手素材，適當改編幫助學生拓展思維，挖掘母題的內涵和外延，積累豐富的解題體驗，總結出一題多解、一法多題的通性、通法.俗話說的好，“做錯題目不可怕，題后反思是王道”.“思中學，學中思”，通過解題反思提高解題能力，達到做一題、會一類的效果，進而增強學習數學的信心.