由一道習題的講評引發的思考

☉浙江省溫州市甌海區外國語學校 陳乘風

習題課教學是初中數學最常見的一種課型，如何優化習題講評，借助于習題講評提升學生的數學核心素養呢？本文借助于具體的實踐談一談筆者的思考，望能有助于初中數學習題課教學實踐.

一、習題呈現與解析

習題：一矩形紙片OABC如圖1所示，若OA=7，OC=5，在BC邊上取一個動點D（圖中未標出），現將△OCD沿直線OD折疊，若頂點C折疊后落于直線l：y=x+7上時，對應點記作E、F點，若頂點C折疊后的對應點落于OA邊上，將其記作G點.

（1）求E、F兩點的坐標.

（2）求經過G、E、F三個點的拋物線的解析式.

（3）若點C折疊后的對應點落于直線l上，求CD的長度？

（4）在問題（2）中，拋物線上是否存在一點P，使△EFP成直角三角形？如果你認為存在，則請求出P點的坐標？如果你認為不存在，請給出你分析的理由.

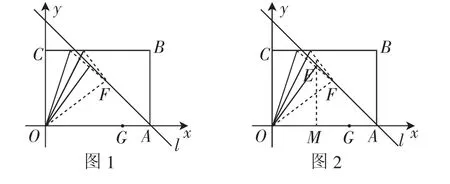
解析：（1）過點E作EM⊥x軸于點M.如圖2所示，則OE=OC=5.設點E（x，-x+7），可得EM=-x+7，OM=x.在Rt△OME中，OM2+EM2=OE2.則x2+（-x+7）2=52，解得x=3或x=4.當x=3時，y=-x+7=4；當x=4時，y=-x+7=3.

則E、F兩點的坐標為E（3，4）、F（4，3）.

（2）設經過G、E、F三個點的拋物線的解析式為y=ax2+bx+c.將E（3，4）、F（4，3）、G（5，0）代入，可得：

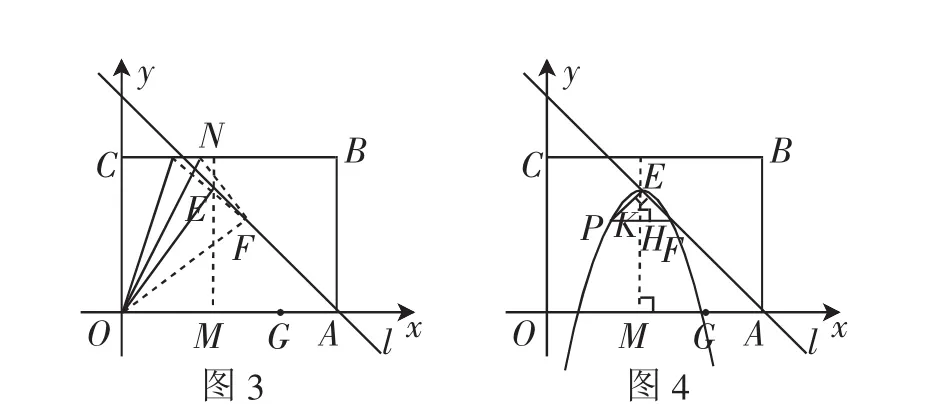
（3）若點C折疊后落在點E上，如圖3，設點C與動點的距離CD=m.過E作ME⊥x軸于點M，交BC于點N.

由E（3，4），可知CN=3，EM=4，EN=5-4=1，DN=3-m，DE=CD=m.

在Rt△DNE中，DE2=DN2+NE2，即m2=（3-m）2+12，解得

（4）設拋物線上存在一點P，使△EFP成直角三角形，設點P的橫坐標為x，則其坐標為（x，-x2+6x-5）.

若PF是斜邊，作FH⊥EM于點H，作PK⊥EM于點K，如圖4所示.

同理，若PE是斜邊，可求得點P（1，0）.

若EF是斜邊，以EF為直徑作一個圓，則點P在圓上，但該圓與拋物線的交點只有E、F，因此也就不存在能夠使△EPF為直角三角形的點P.

二、該習題的講評策略

這道題如何講評才能起到良好的教學效果呢？筆者認為可以從如下幾個方面入手.

1.在實踐中建模

這道題在學生審題的過程中，如果缺乏空間想象能力，往往會有諸多困惑，但基本上都集中在點C折疊后的對應點C′上.

困惑1：△OCD沿OD折疊時，點C折疊后的對應點（可以將其記為點C′）是否一定落在直線l：y=-x+7上？分析影響其落在直線上的因素有哪些.

困惑2：點C′的位置存在幾個？

如何解惑呢？最好的辦法就是讓學生實驗，動手實踐自主定位點C′.

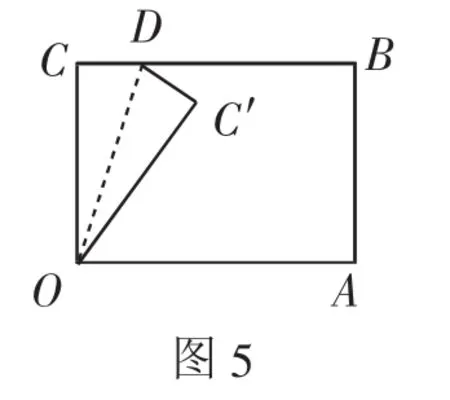
實驗：請每組學生提供一張矩形白紙，要求學生經過O點自主折疊矩形一角，如圖5所示，然后在學生實踐的基礎上，采用提問的方式進行建模.

問題1：你在折疊白紙時遇到了什么問題？（筆者在巡視中發現，有相當一部分學生遲遲不敢下手折疊白紙，詢問后發現，他們不敢下手的原因是事先沒有約定好沿什么方向折疊.這的確是一個問題，因為缺失了該條件，折出來的折痕就會不同.）

問題2：折疊好后，相互之間比較一下，看一看大家折的有什么異同.（所有學生折出來的結果有一點是相同的，即折痕均經過點O，其他就不一樣了，正因為有這樣的差異，可以及時地引導學生進行多種折疊方法的探究與比較.）

問題3：（巡視中尋找目標學生）請你談一談在過點O折疊矩形一角這一實驗過程中有怎樣的感悟.

生：我們嘗試了很多種折疊，我們發現折疊的過程相當于將線段OC繞點O進行旋轉，所以C點肯定落在以O為圓心的一個圓周上，圓的半徑為OC（如圖6）.

在學生有了上述實踐與感悟后，再一次引導學生回到最初兩個困惑的討論中來，并在討論中有新的發現：點C和直線l的位置關系的即為直線和圓O的位置關系，同時圓心與直線的距離d和（rOC）之間的大小關系又對直線和圓的位置關系有影響，這是解決此題的突破口所在.根據題意我們可以求得，繼而判斷直線和圓存在兩個交點，如圖7所示，設交點為E、F.

找到了定點E、F，AE、AF就必然為定值.如此一來，我們探究的問題又可以進一步轉化為定點E、F到矩形OABC的頂點、邊界、靜態線段距離的問題探究.由此作圖，如圖8所示，在矩形OABC中，現經過頂點O的某一直線折一個“拐”并使點C的對應點落在邊MN上.

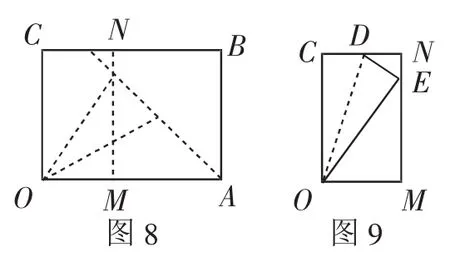
引導學生在圖8中找到相關已知線段，然后對圖形進一步提煉得到圖9所示模型，完成問題的轉化：如圖9所示，在矩形OMNC中，過點O沿直線OD折疊一個角，D點的對應點恰巧落在直線MN上的E點，且已知EN=1，求CD的長.如此轉化后，熟悉的翻折模型自然浮現在學生大腦，原有認知被有效喚醒：這是折疊圖形使其一個角的頂點的對應點位于某條邊所在直線上的問題，該問題學生是熟悉的，運用勾股定理即可完成求解.

2.在直觀想象中建模

數學問題的解決需要學生建模，除了上述在實踐過程中完成建模和問題的轉化，我們還應該更多地引導學生進行直觀想象和科學思維，運用數學思想方法完成問題的簡化.

例如，第（4）個問題我們除了采用上文解析中的方法，借助直觀想象通過數學建模的方式也可以解決，而且問題的解決會變得更簡單、直觀.

從△EFP為直角三角形的可能性出發，根據直角頂點的差異可以分成三種類型討論：

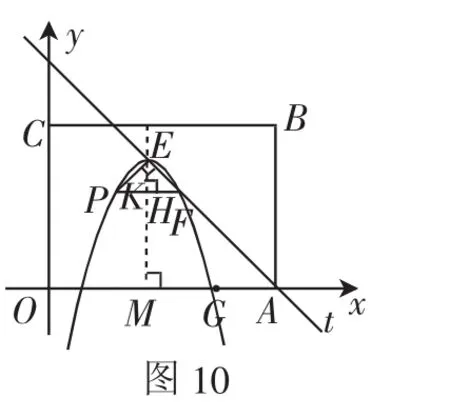
情形1：點E為直角頂點，作FH⊥EM于點H，并延長FH與拋物線交于點P，如圖10所示，從已知條件出發，再觀察圖形，可得△FHE為等腰直角三角形，得∠FEH=45°.

再結合拋物線的對稱性，可得∠FEH=∠PEH=45°.則∠FEP=90°，所以點P滿足條件，點P和點F軸對稱，則F（4，3），所以P（2，3）.

情形2：點F為直角頂點，我們可以過點F作FP⊥EF，并與拋物線相交于點P′，再借助想象，借助勾股定理模型、勾股定理的逆定理最終推出△P′EF是直角三角形，得到P（1，0）.

情形3：將P作為直角頂點（解法與前文解析相同）.

總之，在數學問題的解決過程中，我們要盡可能調動學生多個感官的參與，在習題講評的過程中，應該注重思維可視化引導，發展學生直觀想象、猜想和推理的能力，在解決問題的過程中感受數學的形態美、邏輯美，發展學生嚴謹地分析問題、解決問題的態度，在不斷探索問題解決方法的過程中完成數學核心素養的提升.