靠船下篙，順水推舟，船行千里
——對2018年南通市中考數學第28題的分析與思考

☉江蘇省如皋經濟技術開發區實驗初中 章小健

今年我有幸參加了2018年南通市中考數學試卷的評閱工作.今年數學試卷以“課標”為依據，以“教材”為題源，充分體現了“遵循課標，緊扣課本，重視能力，貼近生活，控制難度”五大命題原則.第28題（壓軸題）以教材“最短路徑模型”構造新定義，考查對定義的理解、運用和探究，試題入口熟悉又寬敞，解法多樣，探索性強，是課本經典題目和題型的升華，讓經典題有了新意，更有活力.

本文擬對第28題進行深入分析，并結合試卷中所反饋的信息，談談對數學教學的啟示與思考.

一、試題呈現

【定義】如圖1，A、B為直線l同側的兩點，過點A作直線l的對稱點A′，連接A′B交直線l于點P.連接AP，則稱點P為點A、B關于直線l的“等角點”.

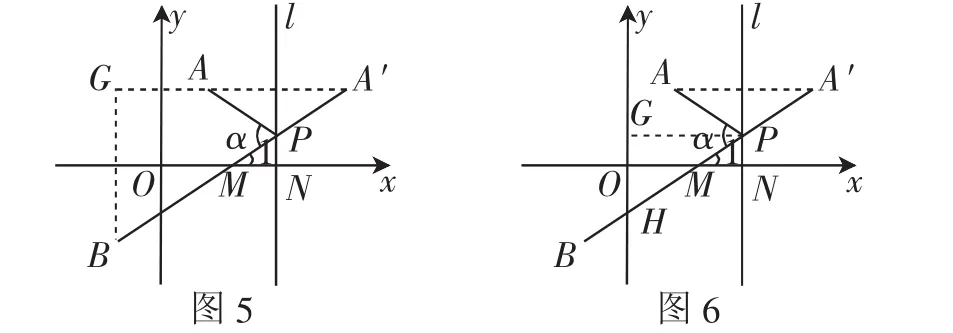
（2）若直線l垂直于x軸，點P（m，n）是點A、B關于直線l的等角點，其中m＞2，∠APB=α，求證：tan

（3）若點P是點A、B關于直線y=ax+b（a≠0）的等角點，且點P位于直線AB的右下方，當∠APB=60°時，求b的取值范圍（直接寫出結果）.

二、參考答案

（1）C.

（2）如圖3，因為點P（m，n）是點A、B關于直線l（直線x=m）的等角點，由定義可知A、A′關于直線x=m對稱，所以PA=PA′，∠APG=∠BPH.

所以∠A=∠A′.又∠APB=∠A+∠A′=α，所以∠A=

作BH⊥直線x=m，垂足為H.

可得∠AGP=∠BHP=90°，所以△AGP △BHP，則

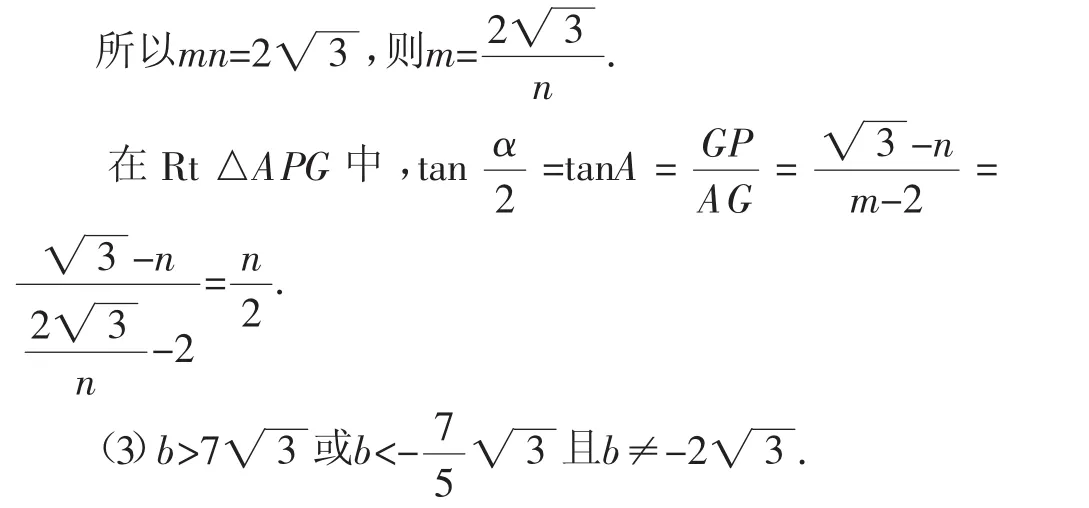
三、優秀解法

本題第（2）問，敘述簡約，呈現簡潔，解法靈活多樣，現給出不同于參考答案的一些解法，供參考.

解法1：如圖4，延長A′A交y軸于點G.設A′B交y軸于點H，連接GH.

因為點P（m，n）是點A、B關于直線（l直線x=m）的等角點，由定義可知A、A′關于直線x=m對稱，可求得A（′2m-2，），PA=PA′，所以∠PAA′=∠A′.又∠APB=∠PAA′+∠A′=α，所以∠A

設直線A′B的解析式為y=kx+b（k≠0）.把A（′2m-2，）、B（-2，-）代入，得：

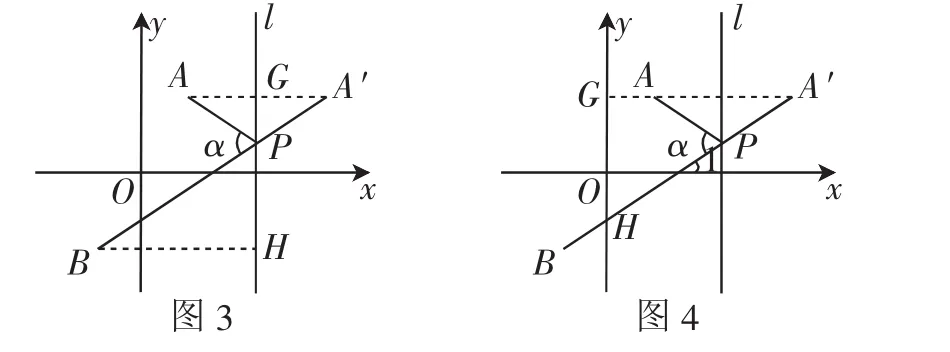
解法2：如圖6，作PG⊥y軸于點G.設直線A′B交y軸于點H，則∠GPH=∠A′.

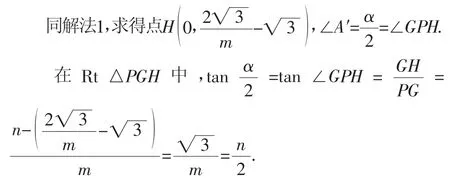
分析：解法1和解法2中，學生利用點的坐標求出了帶參數的直線解析式，再利用直線的解析式求出與坐標軸的交點的坐標，利用坐標表示出線段的長度（用含m或n的代數式表示），從而在直角三角形中，利用三角函數的定義求解.此方法學生易下手，貼近學生思維.

解法3：如圖7，設A′B交x軸于點M，直線x=m交x軸于點N，連接MN.

yA′+yB=0，所以A′、B關于點M對稱.

由中點坐標公式，求得xM=m-2，所以MN=2.

分析：學生緊靠定義實現條件的轉化，求出點A′的坐標，發現B、A′關于點M對稱，從而求出M點的坐標，進而求出MN的長，根據要證結論，考慮包含的直角三角形，直接利用定義轉化成線段的比值，問題得證.解法獨特，頗具新意.

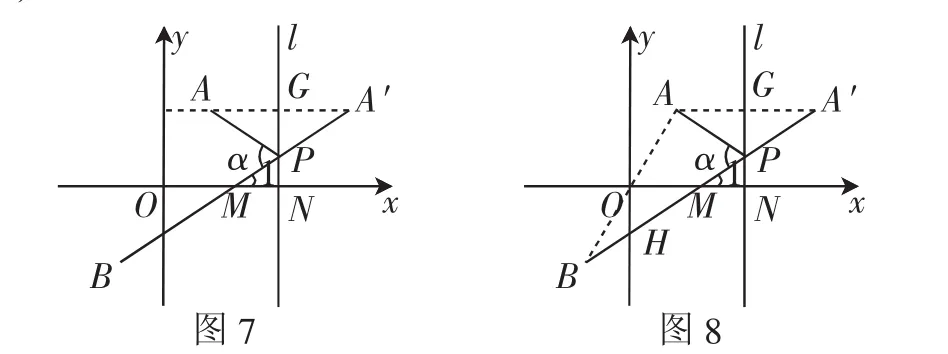
解法4：如圖8，連接AB.

yA′+yB=0，所以A′、B關于點M對稱.

O、M分別是BA、BA′的中點，所以OM是△BAA′的中位線.

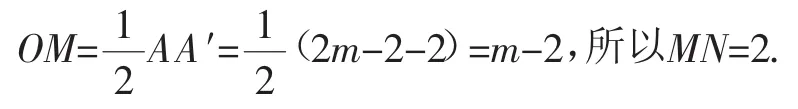
解法5：如圖9，過A′、B分別作x軸和y軸的垂線，交于點H，A′H交x軸于點N.

yA′+yB=0，所以A′、B關于點M對稱，M是BA′的中點.又N為AH的中點，所以MN是△A′BH的中位線.

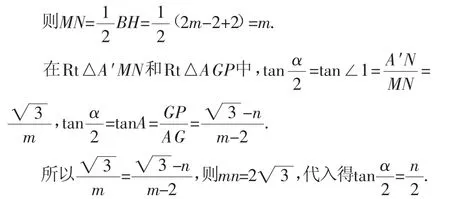
分析：解法4和解法5中，學生從定義出發，求出點的坐標，再由點的坐標發現對稱，進而構造出三角形的中位線，利用中位線求出OM或MN的長，使問題得證.

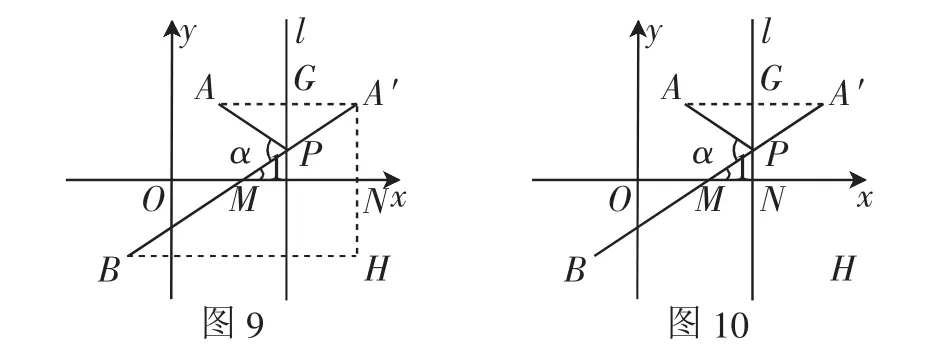
解法6：如圖10，因為點P（m，n）是點A、B關于直線l（直線x=m）的等角點，由定義可知A、A′關于直線x=m對稱，可求得點A（′2m-2，

分析：解法6和解法7思路簡潔，但兩種解法中都應用到直線的斜率k的計算公式解法7中還用到了直線的夾角公式和正切倍角公式.學生需要對公式有清晰的認識和理解，并會運用公式，解法7運用了歸納推理和演繹推理相結合的探究方法，這可能得益于創新班學生之筆.

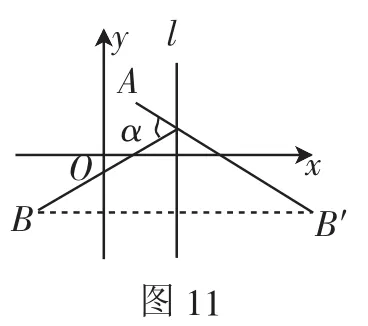
在眾多考生中也有不少考生考慮作點B的對稱點，構造“等角點”（如圖11），其他解法同上文.

四、試題評析

本題以課本例題“最短路徑模型”構造新定義.學生感覺模型熟悉，定義簡單，其實就是舊知的一個創新.這與近幾年南通中考最后一題相比有了很大的變化，本題不再是以拋物線或雙曲線為載體，而是根據學生熟知的模型，重新定義，考查學生自主學習、知識遷移與探究的能力.

第（1）問是第（2）問的具體情境.第（1）問的解法為第（2）問提供了解題的思路和方法，意在引導學生由淺入深向第（2）問和第（3）問過渡，安排合理，為學生探究鋪路.第（2）問難度不大，但方法靈活，主要是幫助學生克服畏難的心理障礙，為第（3）問探究和創新樹立信心.第（3）問緊扣定義，確定P點的軌跡，從而確定直線的位置.

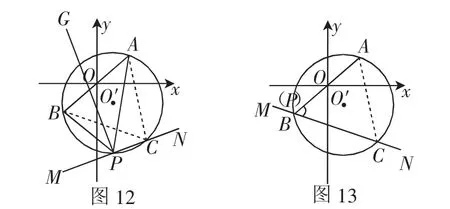
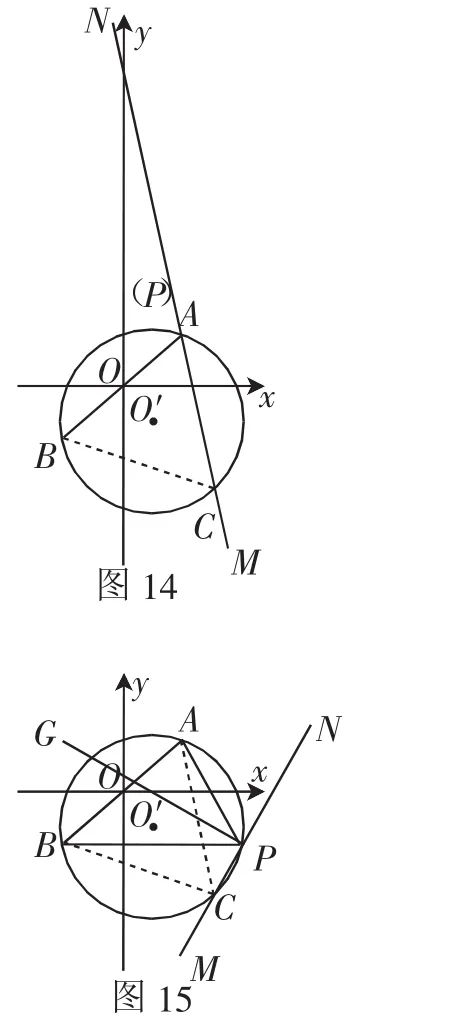
如圖12，因為AB長為定值，且∠APB=60°也是定值，所以點P始終在以AB為邊的等邊三角形的外接圓上.故可在直線AB的右側以AB為邊作等邊△ABC，再作△ABC的外接圓⊙O′.根據“等角點”的定義，P是點A、B關于直線y=ax+b（a≠0）的等角點.故直線y=kx+b與直線PA、PB所成銳角相等，即∠BPM=∠APN.又∠APB=60°，所以∠BPM=∠CPN=60°.故可作∠APB的角平分線PG，過P點再作PG的垂線MN即為直線y=ax+b.在⊙O′中，∠APN=∠ABC=60°，所以MN必過點C，即直線y=ax+b必過點C.考慮點P在直線AB的右下方，且點P在⊙O′上，我們可以把直線MN繞著點C旋轉尋找點P的可能位置，可以發現經過點B和點A時（如圖13和圖14），即為第（3）問問題探究的極端情況.當直線y=ax+b平行于x軸時（如圖15），a=0，與題意不符，故排除.

當點P、A重合時，直線y=ax+b（a≠0）過點A、C，求得（如圖14）.

第（3）問要求學生結合圖形探究點和直線的運動變化，觀察、分析、歸納、推理，發現結論.優秀學生能展示自己的數學智慧和創新能力，使該題起到了選拔的作用.

五、教學啟示

從考生卷面及得分看，對于第（1）問，多數考生可得全分，第（2）問和第（3）問問題較多，一些學生不能把定義的內涵應用于新的情境，如本題中“等角點”的定義，學生未能把等角的條件轉化利用，構建相似，一些學生不能利用基本模型，如過B點作直線x=m的垂線，構造“X型”等數學模型構造相似，建立邊長關系，不會求解含字母系數的直線的解析式，不會計算與坐標軸的交點的坐標及用含字母m或n的代數式表示線段的長.因此，對數學教學有以下啟示.

1.關注基礎，理解定義的內涵，實現知識遷移

本題第（1）問和第（2）問難度不大，但許多考生不能把新定義的知識遷移.我們在平時教學中，必須加強定義的理解，掌握定義的內涵，夯實基礎.對于新定義的教學，我們首先要深刻理解概念，然后提煉問題結構，再從數形結合的角度揭示問題結構.像上文中找出P點在以AB為邊的等邊三角形的外接圓上，借助圓研究.課堂教學中，積極引導學生獨立思考、反思質疑，加強互動.關注“知識與技能”的發生和發展過程，在應用中不斷鞏固和深化“雙基”，從而讓學生真正理解定義的內涵，實現知識的遷移.

2.立足教材，重視基本模型，提升解題能力

教材與教材中的一些數學模型，是中考命題的藍本，同時是天然的好素材.每年都有大量的新穎試題直接源于教材，或以教材中提供的一些數學模型為基礎，經過改造整編、移植借鑒.因此，在平時的教學中，立足教材，重視基本模型，要理解基本圖形的關鍵特征，找準基本圖形的核心要素.試題中有的基本圖形處于潛伏狀態，有時需要通過補充嘗試激活基本模型.如上文中作垂直構造“類似K型或X型或A型”模型.我們要讓教材成為學生鞏固知識、觀察、分析、思考、探究問題、發展能力、掌握思想方法的重要渠道，真正實現從“教教材”到“用教材教”的飛躍，以提升解題能力.

3.注重發散，加強思維拓展，培養創新能力

創新思維是時代發展的需要，沒有創造性思維的培養就造就不了創新型人才.在平時教學中，鼓勵學生再次發現，重新組合，讓學生在知識的自主建構中，張開思維和想象的翅膀，尋找問題解決的策略，應盡可能地發散學生的思維.發展學生的求異思維，使其學會從多角度、全方位考慮問題，培養其創新能力.在新定義考題解題教學中，遇到一些直接寫結果的設問時，要充分展開思維過程，通過數形結合、動畫展示的方式，讓學生對解題思路的理解有更直觀的認識.

在試卷評閱中發現，有部分考生解題不規范，格式不簡明，抓不住得分點.如有學生用P（m，n）、B（-2，-）求直線的解析式，解析式中含兩個參數字母，為后續解題設置了障礙.還有考生把表示成，導致錯誤.還有代數式的變形、化簡、計算錯誤較多.所以平時教學中，一定要嚴格要求學生，規范解題格式和書寫格式，養成正確的解題習慣，提高學業水平，提升數學素養.