矩形內接正三角形問題的探究

☉江蘇省南京市金陵中學仙林分校中學部 毛亞玲

江蘇省南京市2017年中考第27題以學生熟悉的折紙為背景，結合“軸對稱、旋轉與位似”及勾股定理、特殊三角形，綜合運用操作探究、猜想證明、語言呈現、線段求值解決矩形內部最大正三角形問題，尤其第（3）問關于矩形內部最大正三角形的操作、計算、作圖難度系數只有2，而此類問題與教學緊密相連，學生非常感興趣，如何突破難點顯得尤為重要.筆者對此類問題進行了梳理、總結.

一、試題呈現

題目：（2017年江蘇·南京卷第27題第（3）問）（3）已知矩形一邊長為3cm，另一邊長為a cm.對于每一個確定的a的值，在矩形中都能畫出最大的等邊三角形.請畫出不同情形的示意圖，并寫出對應的a的取值范圍.

二、問題解決

探究1：任意矩形都有一個最大的內接正三角形.

對于問題（3），我們不妨假設矩形的一邊長為a，另一邊長為b，由此我們可以探討對于任意一個矩形而言，其內部是否存在面積最大的正三角形，以及最大面積是多少的問題.

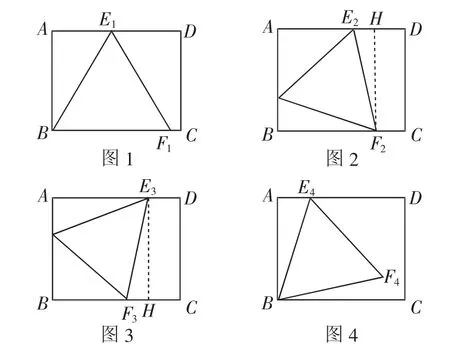
分析：在圖1所示的矩形ABCD中，設AB=a，BC=b.不妨設b＞a，考慮到面積最大，應盡量使正三角形的頂點在矩形的邊上，分如下四種情況討論.

情形1：如圖1所示，正三角形的三個頂點中的一個頂點與矩形頂點重合，另外兩個分別在矩形較長的一組對邊上.

情形2：如圖2、圖3所示，正三角形的三個頂點中的一個頂點在較短邊上，另外兩個分別在矩形較長的一組對邊上.

在圖2中，過F2作BC的垂線交AD于點H，設∠E2F2H=α，由題意知α＜30°，則cosα＞cos30°.

在Rt△E2F2H中，，此種情況舍去.

同理，圖3這種情況也可以得出上述結論.

情形3：如圖4所示，正三角形的三個頂點中的一個頂點與矩形頂點重合，另外一個在矩形較長的邊上，第三個在矩形內部.

在圖4中，設∠ABE4=β.由題意知，β＜30°，則cosβ＞cos30°.

在Rt△ABE4中，，此種情況舍去.

情形4：如圖5所示，正三角形的三個頂點中的兩個頂點與矩形較短邊頂點重合，第三個在矩形內部.

結論1得證.

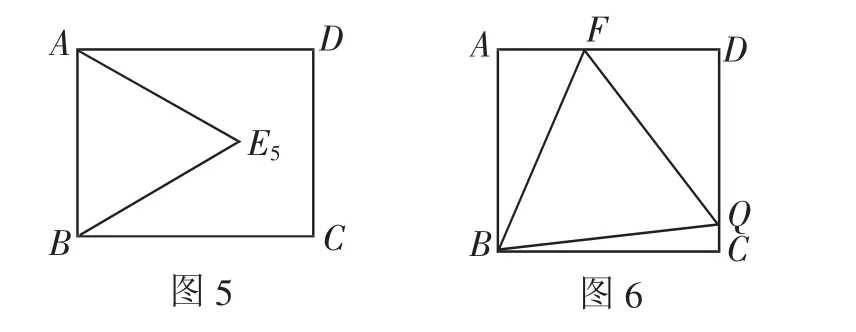
下面我們可以考慮幾種特殊情況：

（2）當任意矩形為正方形，由結論2我們得到正方形內接最大正三角形面積為正方形邊長平方的

由結論2我們可以考慮正五邊形、正六邊形……正n邊形的內接最大正三角形問題，以正五邊形和正六邊形為例，當正三角形一邊與正多邊形一邊重合時，此時面積最小，固定正三角形的一個頂點，拉著邊往上移動，正三角形的面積逐漸增大，直到正三角形的第三個頂點落在正多邊形邊上時，面積最大并且唯一，此時的圖形是軸對圖形.我們設正五邊形的邊長為a，可以得到此時正五邊形內接最大正三角形面積為同理，正六邊形邊長為a的話，它的內接最大正三角形面積為，并且我們發現此時正三角形的頂點正好在正六邊形的間隔開的三個頂點上.以此類推，若是正九邊形的話，其最大的內接正三角形的頂點也是在間隔開的三個頂點上.那么，凡是邊數是3的倍數的多邊形，其內接最大的正三角形的頂點一定在其等距間隔開的三個頂點上.而在兩個倍數之間的正多邊形，可采取分割多邊形成三角形的思想和正弦定理，求出正三角形的邊長，面積即可得.

三、實踐操作

探究2：任意矩形內接正三角形的尺規作法.

下面我們可以嘗試用尺規作圖的方式將這三種情況通過作圖作出來.定理1和定理2的作圖比較容易，這里不再贅述.定理3在確定了a與b的情況下，tanα的值已知，在銳角范圍內α的值也就唯一確定，從而矩形內部的正三角形也唯一確定.

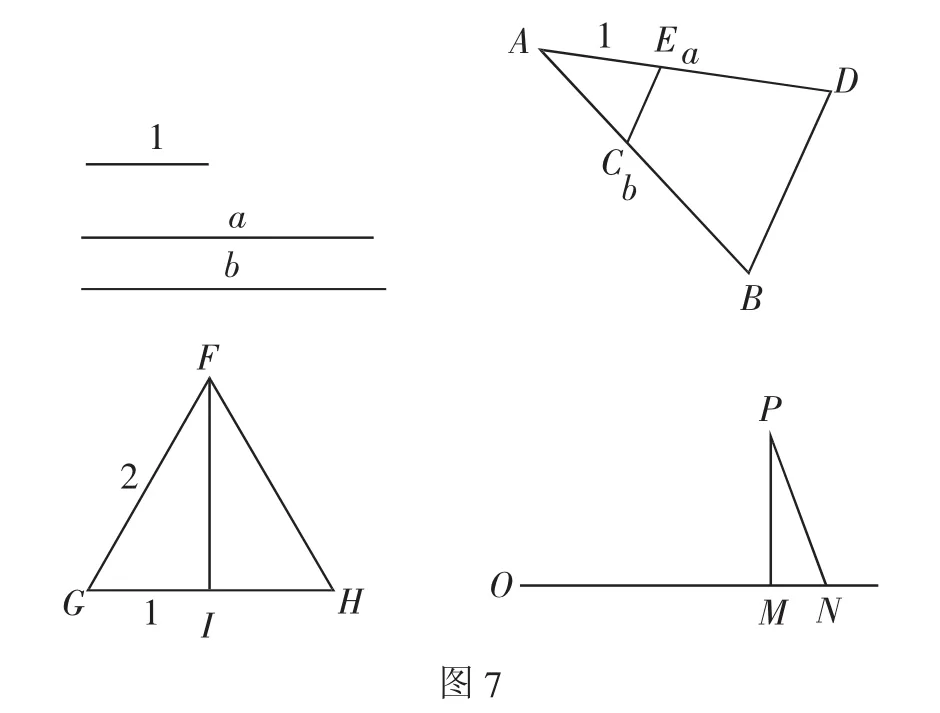
舉例：如圖7，設單位長度為1，一邊長a=2.4，另一邊長為b=2.5（a與b可測），可利用如下方法尺規作圖作出α的大小.

第一步：利用相似三角形的性質：如圖7，AD=a，AE=1，AB=b，可得到，同時利用等邊三角形作出

四、相關拓展

探究3：邊長為a的正三角形的外接矩形面積的最小值.

要使得正三角形的外接矩形最小，應使得正三角形的邊或頂點在外接矩形的邊上，所以我們得到如下兩種情況：

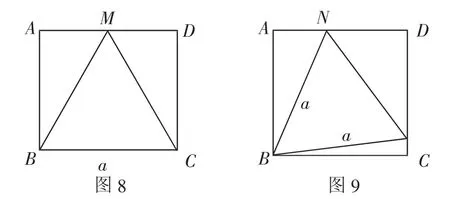
情況1：在圖8中，正三角形MBC的一邊BC與矩形的一邊重合，此時外接矩形的另一條邊AB即為正三角形MBC的高，則BC=a，，所以S=AB·ABCD

情況2：在圖9中，設∠RBC=θ，則∠ABN=30°-θ.

在Rt△RBC中，BC=a·cosθ.

同理，在Rt△ABN中，AC=a·co（s30°-θ）.

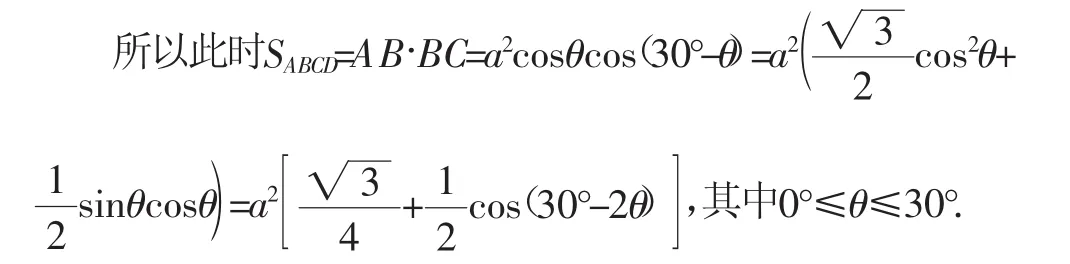
要使得矩形ABCD的面積最小，就要使cos（30°-2θ）最小.根據余弦函數的單調性，可知當30°-2θ最大，即θ=0°時滿足題意.此時與情況1完全一致.于是我們得到如下結論：