核心素養(yǎng)視角下教學(xué)設(shè)計的實踐與思考
——以浙教版八年級下冊2.1“一元二次方程”為例

☉浙江省衢州市衢江區(qū)杜澤鎮(zhèn)初級中學(xué) 徐建兵

在2018年浙江省數(shù)學(xué)疑難問題解決研訓(xùn)中，首都師范大學(xué)數(shù)學(xué)科學(xué)院王尚志教授作了“核心素養(yǎng)與初中數(shù)學(xué)教學(xué)”的報告，報告指出，課程改革主要的變化是從“以知識為本”轉(zhuǎn)變?yōu)椤耙詫W(xué)生為本”，建議教學(xué)實踐中要不斷發(fā)現(xiàn)、提出問題，分析、解決問題，提高教與學(xué)的效率.數(shù)學(xué)核心素養(yǎng)是學(xué)生在接受相應(yīng)學(xué)段的教育過程中，逐步形成的適應(yīng)個人終身發(fā)展和社會發(fā)展需要的數(shù)學(xué)思維品質(zhì)與關(guān)鍵能力.數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、直觀想象、數(shù)學(xué)運算、數(shù)據(jù)分析這六個核心素養(yǎng)的提出，是課程從知識立意發(fā)展到能力立意，再到素養(yǎng)立意的一個過程，它是數(shù)學(xué)學(xué)科教育“品質(zhì)”不斷完善的產(chǎn)物.數(shù)學(xué)中每一個核心素養(yǎng)有其自身的獨立性，也有它們的整體性，相互交融滲透.如何通過有效設(shè)計課堂教學(xué)提升學(xué)生的數(shù)學(xué)核心素養(yǎng)，這是筆者一直思考的問題.本文以浙教版八年級下冊2.1“一元二次方程”為例，談?wù)剶?shù)學(xué)核心素養(yǎng)視角下課堂教學(xué)設(shè)計的一些思考.

一、有效設(shè)計整體結(jié)構(gòu)，承載數(shù)學(xué)核心素養(yǎng)

“一元二次方程”是浙教版八年級下冊第二章第1課時，學(xué)生已經(jīng)學(xué)過一元一次方程、二元一次方程和分式方程，具備類比研究和自主學(xué)習一元二次方程相關(guān)知識的能力.對于這節(jié)一元二次方程的概念課，筆者意在讓學(xué)生通過學(xué)習，經(jīng)歷一元二次方程概念的發(fā)生過程，理解一元二次方程一般式的形成過程.根據(jù)學(xué)生原有的學(xué)習經(jīng)驗和認知基礎(chǔ)，以培養(yǎng)學(xué)生的數(shù)學(xué)建模、數(shù)學(xué)抽象、數(shù)學(xué)運算、邏輯推理等核心素養(yǎng)為目標，圍繞著“列”“研”“納”“化”“判”五個教學(xué)環(huán)節(jié)展開教學(xué).通過“列”，讓學(xué)生在尋找量與量的關(guān)系中，提升數(shù)學(xué)建模素養(yǎng)；通過“研”，從“式、元、次”三個維度類比一元一次方程的學(xué)習過程，在自我構(gòu)建一元二次方程的概念中，提升數(shù)學(xué)抽象素養(yǎng)；通過“納”，在學(xué)生體驗歸納一元二次方程一般式的過程中，提升數(shù)學(xué)抽象素養(yǎng)；通過“化”，在將一元二次方程轉(zhuǎn)化成一般式的恒等變形過程中，提升數(shù)學(xué)運算素養(yǎng)；通過“判”，在學(xué)會推理判斷一元二次方程的根和學(xué)會待定系數(shù)法中，提升數(shù)學(xué)邏輯推理素養(yǎng).整堂課圍繞著“列”“研”“納”“化”“判”這五個環(huán)節(jié)，讓學(xué)生在掌握知識的同時，體會學(xué)習的方法，形成學(xué)習的能力，提升數(shù)學(xué)核心素養(yǎng).

二、有效設(shè)計教學(xué)內(nèi)容，提升數(shù)學(xué)核心素養(yǎng)

1.在列方程中提升數(shù)學(xué)建模素養(yǎng)

數(shù)學(xué)建模是對現(xiàn)實問題進行數(shù)學(xué)抽象，用數(shù)學(xué)語言表達問題，用數(shù)學(xué)知識與方法構(gòu)建模型解決問題的過程.在我們的生活中，有許多的量，有等量關(guān)系也有不等量關(guān)系.這些關(guān)系的確定是解決問題的關(guān)鍵，需要學(xué)生具有數(shù)學(xué)建模的良好素養(yǎng).讓學(xué)生從問題背景中學(xué)會尋找量與量的關(guān)系列出方程，有利于學(xué)生數(shù)學(xué)建模素養(yǎng)的提升.

活動1：列

請同學(xué)們閱讀下列問題，思考問題中量與量的關(guān)系，列出問題中關(guān)于未知數(shù)x的方程.

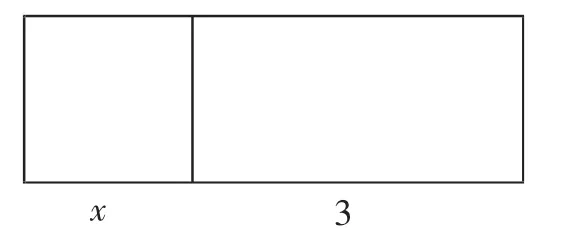
圖1

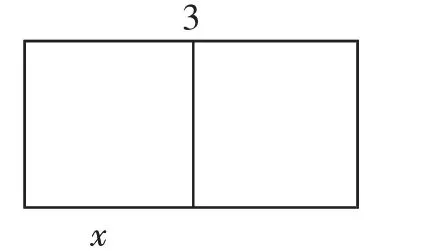
圖2

（1）一張周長12cm的長方形彩紙，長比寬多2cm，設(shè)長方形的長為x cm，可列出方程______；（2）把面積為8cm2的一張彩紙分割成如圖1所示的正方形和長方形兩個部分，設(shè)正方形的邊長為x cm，可列出方程______；（3）如圖2，長方形彩紙的面積是正方形的2倍，設(shè)正方形的邊長為x cm，可列出方程______；（4）一底面是正方形的長方體，體積為27cm3，高為3cm，設(shè)正方形的長為x cm，可列出方程______；（5）一種彩紙原價5元，經(jīng)過兩次漲價，現(xiàn)在售價為7元，設(shè)兩次漲價的平均增長率為x，可列出方程______.

答案：（1）2（x+x-2）=12；（2）x2+3x=8；（3）2x2=3x；（4）3x2=27；（5）5（1+x）2=7.

思考：“列出下列問題中關(guān)于未知數(shù)x的方程.（1）把面積為4m2的一張紙分割成正方形和長方形兩個部分，求正方形的邊長.設(shè)正方形的邊長為x m，可列出方程：______.（2）某放射性元素經(jīng)2天后，質(zhì)量衰變?yōu)樵瓉淼那笃骄刻斓臏p少率.設(shè)平均每天的減少率為x，可列出方程：______.觀察上面所列方程，說出這些方程與一元一次方程的相同和不同之處.”這是教材呈現(xiàn)的利用兩個方程得出概念的內(nèi)容.一元二次方程概念的形成是學(xué)生抽象思維形成的一個重要過程，學(xué)生需要從具體的方程中抽象出概念，同時為了提升數(shù)學(xué)建模素養(yǎng)，筆者對教材進行處理，選取5個學(xué)生身邊的事例，重點放在學(xué)生尋找“量”與“量的關(guān)系”的方法過程中數(shù)學(xué)建模素養(yǎng)的滲透.教材中第（2）問的放射性元素學(xué)生比較陌生不易理解，為了降低學(xué)生的理解難度，突出教學(xué)的重點，筆者把它改成問題（5）“平均增長率問題”，這5個不同形式數(shù)量關(guān)系的出現(xiàn)給概念形成與一般式的出現(xiàn)提供了更充分的抽象素材.

2.在歸納中提升數(shù)學(xué)抽象素養(yǎng)

數(shù)學(xué)抽象是指舍去事物的一切物理屬性，得到數(shù)學(xué)研究對象的思維過程.表現(xiàn)在從事物的具體背景中抽象出一般規(guī)律和結(jié)構(gòu).在一元二次方程概念和一般式的歸納中承載著數(shù)學(xué)抽象素養(yǎng)的形成過程.

（1）在類比研究歸納概念中提升數(shù)學(xué)抽象素養(yǎng)

活動2：研

觀察方程2（x+x-2）=12、x2+3x=8、2x2=3x、3x2=27、5（1+x）2=7，思考下列問題.

問題1：從以上方程中找出已經(jīng)學(xué)過的方程；

問題2：以前研究學(xué)習一元一次方程時，是從哪幾個維度去研究的？

問題3：請類比一元一次方程的學(xué)習，再次從“式、元、次”三個維度研究，看看這些新方程有哪些共同特征.

問題4：帶著它們的共同特征，用自己的語言描述一元二次方程的概念，并把你的描述與書本概念進行比較，體會數(shù)學(xué)概念表述的準確性.

思考：“方程x2+3x=4和（1-的兩邊都是整式，只含有一個未知數(shù)，并且未知數(shù)的最高次數(shù)是2.我們把這樣的方程叫作一元二次方程.”這是教材呈現(xiàn)概念的方式.倘若讓學(xué)生直接看書本，或許學(xué)生對一元二次方程也會有一定的了解，但是這樣不能培養(yǎng)學(xué)生的自主學(xué)習能力，不能讓學(xué)生體會研究方程的一般過程，不利于學(xué)生數(shù)學(xué)抽象素養(yǎng)的提升.每個一元二次方程是具體的，而一元二次方程的概念是抽象的，如何更好地從具體的方程中抽象出概念，這是概念教學(xué)中筆者經(jīng)常思考的問題.自主學(xué)習是學(xué)生素養(yǎng)形成的必經(jīng)之路，在這個環(huán)節(jié)中，呈現(xiàn)一元一次方程2（x+x-2）=12，意在讓學(xué)生從已有的認知出發(fā)，尋找熟悉的“身影”，在發(fā)現(xiàn)新鮮事物的同時，激發(fā)學(xué)生的求知欲望，在學(xué)習研究一元一次方程方法的基礎(chǔ)上，教會學(xué)生研究方程的 “通法”，通過“式”“元”“次”三個維度進行自主學(xué)習，發(fā)現(xiàn)特征，從它們的特征中抽象出一元二次方程的概念.這是概念自我構(gòu)建的一般過程，也是提升學(xué)生數(shù)學(xué)抽象素養(yǎng)的一種有效策略.

（2）在歸納形成一般式中提升數(shù)學(xué)抽象素養(yǎng)

活動3：納

按照下面的步驟，對方程x2+3x=8、2x2=3x、3x2=27、5（1+x）2=7進行整理，并回答下面問題.

步驟1：對方程左右兩邊進行化簡；

步驟2：把所有項移到左邊；

步驟3：化簡后按照降次排列.

問題1：請同學(xué)們寫出整理后各個方程的二次項、一次項和常數(shù)項.

問題2：請同學(xué)們嘗試用字母表示數(shù)，歸納出一元二次方程的一般式，并思考：這些表示數(shù)的字母有什么特殊的要求嗎？

思考：“一般地，任何一個關(guān)于x的一元二次方程都可以化為ax2+bx+c=0的形式.我們把ax2+bx+c=0（a、b、c為已知數(shù)，a≠0）稱為一元二次方程的一般形式，其中ax2、bx、c分別稱為二次項、一次項和常數(shù)項，a、b稱為二次項系數(shù)和一次項系數(shù).”這是教材對一般式的呈現(xiàn)過程，很多老師也是在課堂中直接生硬地給出一般式，筆者認為任何知識的出現(xiàn)與形成都有其原由和價值，因此在“列”的環(huán)節(jié)中，筆者選擇了前面出現(xiàn)過的x2+3x-8=0、2x2-3x=0、3x2-27=0、5x2+10x-2=0這四個方程，其中包含一次項系數(shù)為0的和常數(shù)項為0的方程，這對于由具體的方程抽像出一般式具有非常重要的意義，更能讓學(xué)生體會教材中“都可以轉(zhuǎn)化為ax2+bx+c=0”的含義，也便于學(xué)生對“系數(shù)”和“項”的理解.筆者在課堂中先讓學(xué)生整理，并找出具體的項和系數(shù)，再從具體的系數(shù)中抽象出系數(shù)a、b和c，讓學(xué)生更好地理解每個系數(shù)的取值范圍，學(xué)生在知其然且知其所以然的同時，提升數(shù)學(xué)抽象素養(yǎng).這與下一環(huán)節(jié)的“化”，形成了從具體到抽象，又從抽象到具體的過程，符合學(xué)生的認知規(guī)律.

3.在提煉轉(zhuǎn)化中培養(yǎng)學(xué)生的數(shù)學(xué)運算素養(yǎng)

數(shù)學(xué)運算是指在明晰運算對象的基礎(chǔ)上，依據(jù)運算法則解決數(shù)學(xué)問題的過程.在一元二次方程一般式的轉(zhuǎn)化中，需要學(xué)生理解運算的對象，掌握運算的方法，探究運算的方向等，它承載著數(shù)學(xué)運算素養(yǎng)的提升過程.

活動4：化

觀察一元二次方程的一般式ax2+bx+c=0（a、b、c為已知數(shù)，a≠0）的特征，嘗試把下列方程化成一元二次方程的一般形式，并寫出它的二次項系數(shù)、一次項系數(shù)和常數(shù)項.

（1）9x2=5-4x；（2）（2-x）（3x+4）=3；（3）4x2=5；（4）3y2+

思考：“例1 把下列方程化成一元二次方程的一般形式，并寫出它的二次項系數(shù)、一次項系數(shù)和常數(shù)項.（1）9x2=5-4x；（2）（2-x）（3x+4）=3.解：（1）移項，整理，得9x2+4x-5=0，這個方程的二次項系數(shù)是9，一次項系數(shù)是4，常數(shù)項是-5.（2）可得-3x2+2x+5=0，這個方程的二次項系數(shù)是-3，一次項系數(shù)是2，常數(shù)項是5.”這是教材中給出的例題，運算是數(shù)學(xué)的核心，加之學(xué)生的運算能力不強的事實，筆者對其進行處理，增加兩個小題，順著前一環(huán)節(jié)的一般式進行轉(zhuǎn)化，朝著轉(zhuǎn)化的目標進行運算.任何一種技能的學(xué)習都有一定的“通法”，計算是一個圍繞結(jié)果恒等變形的過程，課堂中，筆者讓學(xué)生朝著一般式的目標，嘗試進行整理，提煉一般方法，讓學(xué)生在體會去括號、移項、合并同類項的基本過程，在自主學(xué)習與方法交流的過程中培養(yǎng)運算素養(yǎng).

4.在判根和用根中提升邏輯推理素養(yǎng)

邏輯推理是指從一些事實和命題出發(fā)，依據(jù)規(guī)則推出其他命題的思維過程.在一元二次方程根的判斷和用根中蘊含著數(shù)學(xué)的邏輯推理素養(yǎng)的形成過程.

活動5：判

問題：判斷下列各題括號內(nèi)未知數(shù)的值是不是方程的根，寫出推理過程.

練習1：已知一元二次方程2x2+bx+c=0有兩個根x1=1，x2=2，求這個一元二次方程.

練習2：已知關(guān)于x的一元二次方程ax2+bx+c=0（a、b、c為已知數(shù)，a≠0）的一個根是1，求代數(shù)式a+b+c的值.若ab+c=0，你能通過觀察，求出方程ax2+bx+c=0的一個根嗎？

思考：教材呈現(xiàn)解是直接在一元二次方程的概念出現(xiàn)之后，“能使一元二次方程兩邊相等的未知數(shù)的值叫一元二次方程的解（或根）”.同時在練習2中讓學(xué)生判斷未知數(shù)的值x=-1、x=0、x=2是不是方程x2-2=0的根.在例2中設(shè)置了待定系數(shù)法的應(yīng)用：“已知一元二次方程2x2+bx+c=0的兩個根為=-3，求這個方程.解：將x=1=-3代入方程2x2+bx+c=0，得解得，所以這個一元二次方程是2x2+x-15=0.”這樣呈現(xiàn)不夠連續(xù)，因此筆者對教材進行處理，先類比一元一次方程解的概念，讓學(xué)生自主學(xué)習獲取一元二次方程根的概念，同時類比一元一次方程解的判斷進行一元二次方程根的判斷，這順應(yīng)了學(xué)生自主學(xué)習的過程.在認識根的同時與一元一次方程的根進行類比，發(fā)現(xiàn)它們都存在能使等式成立的共性，也發(fā)現(xiàn)一元二次方程好像不是一個根的特殊情況，由此激發(fā)學(xué)生的求知欲望.在判根時書寫推理過程，提升學(xué)生的邏輯推理能力.從問題中書寫判根的推理過程提升學(xué)生的數(shù)學(xué)邏輯推理素養(yǎng).從練習1學(xué)會待定系數(shù)法中體驗一元二次方程一般式的“通式”作用.從練習2的解決中讓學(xué)生明確“解必成立，成立必是解”的屬性.三個問題的解決滲透了數(shù)學(xué)的邏輯推理素養(yǎng).

三、結(jié)語

課堂教學(xué)是核心素養(yǎng)落地生根的重要支點和主要渠道，那么，如何在數(shù)學(xué)課堂教學(xué)中給學(xué)生的核心素養(yǎng)提供個性、全面、可持續(xù)的助力呢？首先，我們教師要做一個“有心人”，教學(xué)的設(shè)計要著眼于學(xué)生的可持續(xù)性.課堂教學(xué)設(shè)計要立足于學(xué)生的長遠發(fā)展，培養(yǎng)學(xué)生適應(yīng)個人終身發(fā)展和社會發(fā)展需要的關(guān)鍵能力和思維品質(zhì)，把數(shù)學(xué)的核心素養(yǎng)蘊育在情境與問題、知識與技能、思維與表達、交流與反思之中.數(shù)學(xué)核心素養(yǎng)與數(shù)學(xué)課程的目標內(nèi)容直接相關(guān)，是在數(shù)學(xué)學(xué)習的過程中逐步形成的.它不是獨立于知識、技能、思想、經(jīng)驗之外的“神秘”概念，而是依托于知識與技能的形成之中.數(shù)學(xué)核心素養(yǎng)有它的整體性，在筆者設(shè)計的五個環(huán)節(jié)中，各類素養(yǎng)也是交錯相融的，數(shù)學(xué)建模中蘊含數(shù)學(xué)抽象，邏輯推理中蘊含數(shù)學(xué)運算，它們是相互滲透的.初中生的思維能力尚處于一個相對較低的層次，他們的認知建構(gòu)，很大程度上要依賴于直觀形象思維，而數(shù)學(xué)學(xué)科又有著強烈的抽象性.因此我們在教學(xué)中要注重發(fā)展學(xué)生的數(shù)感、符號意識、空間觀念、幾何直觀、數(shù)據(jù)分析觀念、運算能力、推理能力和模型思想，注重發(fā)展學(xué)生的應(yīng)用意識和創(chuàng)新意識.課堂要以發(fā)展學(xué)生的核心素養(yǎng)為目標指向，以數(shù)學(xué)知識為載體，以數(shù)學(xué)概念的內(nèi)在邏輯為線索，精心選擇學(xué)習素材，構(gòu)建學(xué)習情境，設(shè)計符合學(xué)生認知規(guī)律的系列活動，引導(dǎo)學(xué)生通過多樣化的學(xué)習方式，掌握數(shù)學(xué)“雙基”，形成數(shù)學(xué)思維.并在運用數(shù)學(xué)知識解決問題的過程中，培養(yǎng)創(chuàng)新精神和實踐能力，從而實現(xiàn)核心素養(yǎng)的發(fā)展目標.