數學核心素養視角下問題情境的實驗研究
——從“將軍飲馬”說開去

☉山東省高青縣實驗中學 王彩霞

數學中的“問題情境”，是一種以激發學生問題意識為價值取向的數據材料和情境信息，是從事數學活動、產生數學行為的條件.核心素養的數學教學理念不僅關注知識本身，還關注知識的文化背景和學生的應用遷移能力.在這種要求下，教師要善于設置問題情境，從生活實際入手，引導學生動手實踐，提高學生的實際運用和思考能力，使學生的數學能力得到有效提升.下面筆者以“將軍飲馬”為問題情境，結合求線段和的最小值的教學，談談如何從問題情境出發，由問題情境展開，讓問題情境貫穿始終，一個背景，一氣呵成，一根主線，一以貫之，直抵教學的全部目標.

一、創設情境

著名的“將軍飲馬”問題：如圖1，有一位將軍騎著馬要從A地走到B地，但途中要到河邊飲馬，則將軍怎樣走才能使總路程最短？

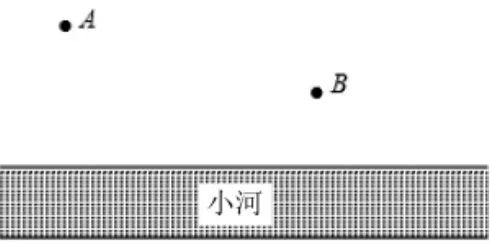
圖1

二、建立模型

我們把河岸看成一條直線，轉化成數學問題就是：如圖2，點A、點B是直線l同旁的兩個定點，在直線l上確定一點C，使CA+CB的值最小.聯系前面學過的線段公理思考這個數學問題怎樣解決.

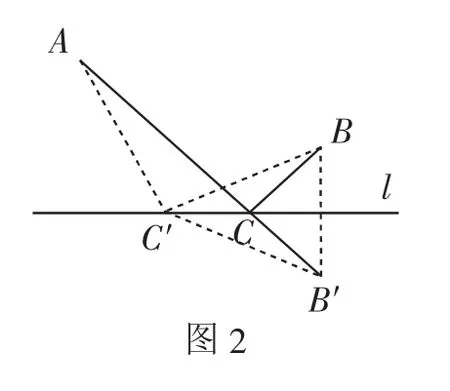
如果A、B兩點在直線l的兩旁，就可以直接利用兩點之間線段最短來解決.怎樣把A、B兩點轉化到直線l的兩旁呢？利用軸對稱的知識，點B關于直線l的對稱點是B′，連接AB′交直線l于點C.連接BC.線段AC、BC就是將軍走的最短路線.這樣兩點在直線同側的問題就轉化成了兩點在直線異側的問題.為什么說這個點C就使CA+CB的值最小呢？

為了證明這個問題，我們不妨在直線l上另外任取一點C′，連接AC′、BC′.

由直線l是線段BB′的對稱軸，得CB＝CB′，C′B＝C′B′.

則AC＋CB＝AC＋CB′＝AB′.

在△AC′B′中，AB′＜AC′＋C′B′，則AC＋CB＜AC′＋C′B.

即AC＋CB最小.

所以AC、BC就是將軍行走的路線，這時所走路程最短.

由此可見，求線段和的最小值的方法就是，找到兩點一線模型，然后通過軸對稱把在直線同側的兩點轉化到直線的兩側，然后利用“兩點之間，線段最短”，使問題迎刃而解.這就是“兩定一動型”的最值問題.

三、拓展模型

數學來源于生活，又服務于生活.數學課程標準把培養和發展學生的應用意識作為基本的理念之一.兩點一線模型還可以進行以下拓展，幫助我們解決生活中的實際問題.

1.一定兩動型

如圖3，將軍騎馬從軍營A出發，先騎馬去草地OX邊吃草，再牽馬去河邊OY處飲水，最后回到軍營，問：這位將軍怎樣走路程最短？

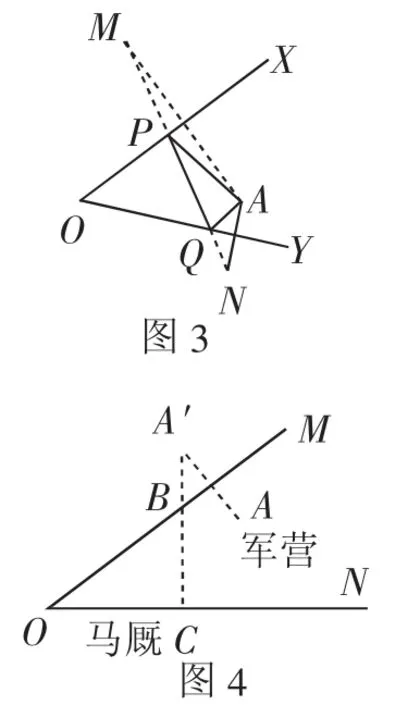
解析：如圖3，利用軸對稱的知識把點A轉化到直線OX、OY的兩側，類比兩點一線模型用線段公理就可以解決了.圖中PA+PQ+QA就是將軍所走的最短路線.

變式：如圖4，將軍騎馬從軍營A出發，先騎馬去草地OM邊吃草，再牽馬去河邊ON外飲水，最后將馬送入河邊上的馬廄C，試確定馬廄C的位置，使將軍行走的路程最短.

解析：該問題即為：在∠MON的內部有一點A，在OM上找一點B，在ON上找一點C，使得AB＋BC最短.先“化折為直”，作點A關于OM的對稱點A′，然后解決如何使A′C最短的問題，即問題轉化為確定射線ON外一點A′到ON的距離的最小值.顯然，可根據“垂線段最短”的性質，確定馬廄C的位置.

兩題的理論依據是不同的，前者利用兩點之間線段最短來求解的，而后者則依據垂線段最短.

2.兩定兩動型

（1）兩線相交

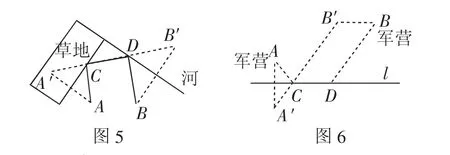
如圖5，A為馬廄，B為帳篷，將軍要從馬廄牽出馬，先到草地邊的某一處牧馬，再到河邊飲水，然后回到帳篷，請你幫他確定出最短路線.

解析：作出點A關于草地的對稱點A′，點B關于河的的對稱點B′，類比兩點一線模型用線段公理求解.如圖5所示，AC—CD—DB即為最短路線.

（2）兩線平行

如圖6，將軍從軍營A出發去河邊l處飲馬，之后牽馬沿河岸散步200米，再回軍營B，問：從河邊何處開始散步，可使整個行程最短？

解析：軍營A與軍營B是兩個定點，問題即為：在直線l上找兩個點C、D，CD=200米，使得AC＋BD最短.若作點A關于l的對稱點A′，連接A′C和BD，會出現兩線段不共線的問題，怎么辦？我們能不能把BD進行相應的平移，使得與A′C共線？

完全可以把BD沿著DC方向向左平移200米，問題迎刃而解.如圖6，作點A關于l的對稱點A′，將點B向左平移CD的長度到點B′（實際上為200米），連接A′B′，交直線l于點C，將點C向右平移CD的長度到點D，則點C、點D即為所求.

變式1：如圖7，將軍每日騎馬從軍營出發，去河岸對側的 望臺觀察敵情，已知河兩岸a、b平行，河流的寬度為30米，請問：在何地修浮橋，可使得將軍每日的行程最短？

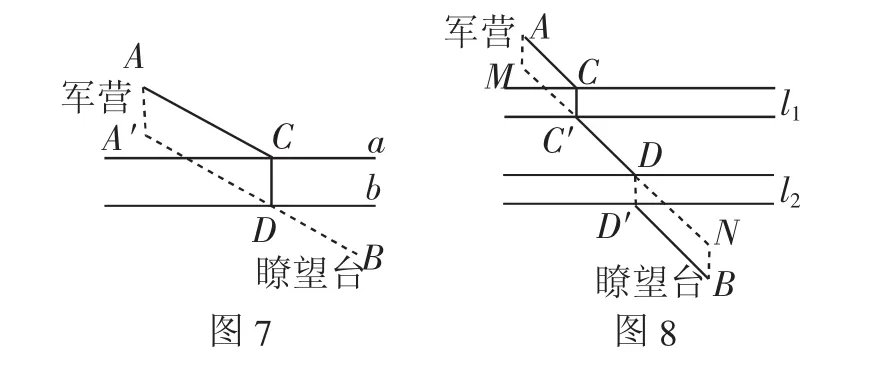
解析：這是著名的造橋選址問題.如圖7，由于橋長CD是一個定值，故我們不妨將橋CD平移轉化成兩點一線的模型.無論橋架在何處，橋CD是必經路線，要使從A到B的折線最短，只需AC＋BD最短即可.于是作AA′⊥直線a，且使AA′的長度等于河寬，連接A′B，交河岸b于點D，作DC⊥河岸a于點C，則建橋CD，可使得將軍每日的行程最短.

這個造橋選址問題在教材中的原題是：“村莊A、B位于一條小河的兩側，若河岸a、b彼此平行，現在要建設一座與河岸垂直的橋，問：橋址應如何選擇，才能使A村到B村的路程最近？”實際上兩題是一樣的，何不對教材進行重組與創新，使之處于一個情境之下？

變式2：如圖8，軍營A與瞭望臺B之間隔著兩條河，假定兩條河互相平行并且河的兩岸筆直，現在要在每條河上垂直于河岸分別建一座橋.應把橋建在什么位置，才能使將軍走的路程最短？

解析：如圖8所示，分別作AM垂直l1的河岸，BN垂直l2的河岸，且使AM的長度等于河l1的寬度，BN的長度等于河l2的寬度，連接MN，分別交兩條河一側于點C′、D，建橋CC′和DD′，連接AC、BD′，那么AC、CC′、C′D、DD′、D′B就是從軍營A經過這兩座橋到瞭望臺的路程，此時路程最短.

這里無論涉及沿河邊散步還是造橋選址問題，都用到了一個平移的思想方法，有的是“水平平移”，有的是“垂直平移”，當然還有“斜平移”，關鍵是抓住定長線段提供的平移方向與平移距離，進行相應的平移之后，即可轉化為“兩定一動型”常規最值問題，然后結合“兩點之間，線段最短”的性質求解.顯而易見，求線段和的最小值的教學，建立兩點一線模型，可使問題得以解決.以“將軍飲馬”為問題情境，不是可以實現“從問題情境出發，由問題情境展開，讓問題情境貫穿始終”的效果嗎？反思一下，相比以“將軍飲馬”為主線，而用平面圖形（比如：正方形、圓中求線段和的最小值）、立體圖形、平面直角坐標系、二次函數或打臺球等材料背景烘托，用一個背景，一氣呵成，一根主線，一以貫之，直抵教學的全部目標，不是更有深意嗎？相比將比較零散、看似不關聯的幾個材料進行不同的變式，用一個材料更能很好地體現它們密切相關，是一個模型的不同側面，從而找到它們的異同點，不人為割裂，從而回歸自然.結合以上兩點一線模型的建構過程，把用數學模型解決實際問題的一般步驟概括如下，供大家參考.

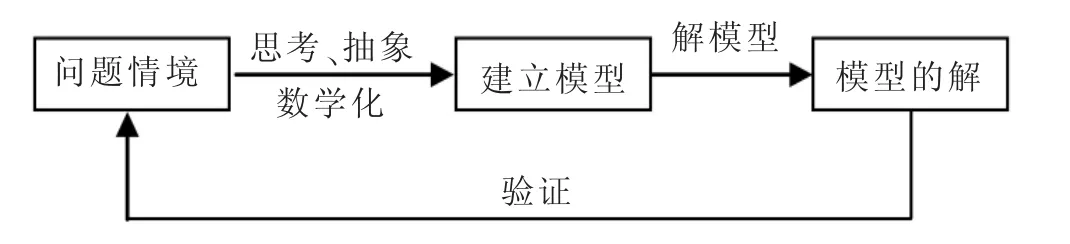
圖9