基于原有認知，培養實踐意識
——新課標背景下初中數學教學實踐與反思

☉江蘇省啟東市百杏中學 浦圣妹

新課標提出發展學生的核心素養，培養更全面的人.那么，對于初中數學教學而言，我們的課堂應該如何變化呢？筆者認為應該更注重學生的學習基礎，應該豐富學生的體驗，有意識地培養學生的實踐意識，增強學生的過程體驗.本文以無理方程的教學為例，就如何具體地實施談幾點思考.

一、創設情境，引導中生成概念

學生都是帶著知識和經驗學習知識的，在學習無理方程之前，學生知道方程，也會“列方程”，為此，我們我們可以從學生的基礎出發設置問題情境，采用實驗和師生對話的方式引出無理方程及無理方程的概念.

實驗情境：老師給每組同學提供了一根30cm長的細鐵絲，現在大家嘗試著將其彎折成一個直角三角形，要求有一條直角邊長為5cm.

設計意圖：這是一個實踐類的問題，學生不加思索，借助于三角板的直角是可以實踐的，但是在彎折的過程中會出現困難，即另外一條直角邊從何處開始“彎折”.繼而生成新的問題.

生成問題：如何求另外一條邊長？

出現了一個未知量，要解決這個問題，學生很自然地會想引入未知數.通常情況下，學生會想到設另一直角邊長度為x cm，借助于勾股定理，學生能夠列出方程：52+x2=（30-5-x）2，即52+x2=（25-x）2（1）.

能列出方程（1）是學生的認知基礎，不僅如此，從該方程中學生還能夠得到斜邊長為此時，可以采用追問的方式進一步引導學生思考.

追問1：除了方程（1），大家還能列出怎樣的方程？

設計意圖：學生從總長度為30cm、一條直角邊長為5cm出發，很自然能夠聯系到斜邊長度應該為30-5-x=25-x，可以得到新的方程：（2）.

追問2：大家觀察方程（2），從我們的原有經驗出發，想一想：方程（2）的左、右兩邊分別指的是什么？猜一猜這樣的方程有什么意義.

設計意圖：追問2是將學生得到方程（2）的思維可視化，方程（2）的左、右兩邊均可以表達彎折出來的直角三角形的斜邊，繼而很自然地歸納方程的實質，即建立等號、列方程的意義，從兩個不同側面對數學問題中同一個量進行表達.當然，同一個數學問題的思考點可以不一樣，找到的同一個量也會不同，可以進一步追問，促進學生對上述認識的理解.

追問3：上述問題，如果我們換一個角度，你還可以列出怎樣的方程？

二、基于生成，比較中深化理解

學生的生成是課堂探究的重要生長點，通過前面的情境創設和引導，學生得到了3個方程，這里有有理方程和無理方程，我們在課堂上引導學生對這3個方程進一步進行比較，能夠深化學生對無理方程的內涵的理解，自主比較得到無理方程的本質特征，印象會更深刻.

師：觀察（1）、（2）、（3）三個方程，你覺得和我們前面學習的方程有怎樣的差別？

設計意圖：方程得到后，學生會發現含有根式且根式下的內容是包含未知數的代數式，以前沒學過，這屬于學生感興趣的地方，如果我們直接灌輸給他們，則印象不深刻，引導學生自己去發現更能夠深化學生對無理方程概念的理解，在學生有了初步判斷后，再拋出一些方程讓學生辨析，能夠促進概念的理解與內化.

練習：判斷下述方程哪些屬于關于x的無理方程.

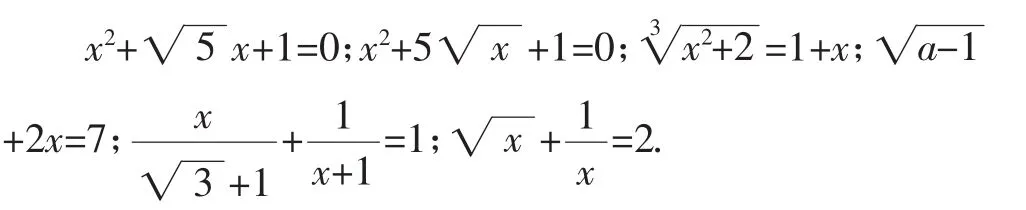
在學生在辨析的過程中有了一定認識后，再進一步引導學生討論前文中涉及的3個方程，將學生的思維點轉移到此類方程如何解的探尋中來.

師：我們大家再來觀察前面得到的三個方程，看看（2）和（3）之間存在的聯系，（1）和（2）之間存在什么聯系？

設計意圖：學生再一次對方程進行比較，比較的過程就是實踐的過程，而且行有所獲，最終學生會發現代數式的變化過程，將方程（3）等價變形可以得到方程（2），將方程（1）的兩邊同時開方可以得到方程（2），在此基礎上，為了防止學生的思維出現片面性，可以進一步追問.

追問4：若a2=b2，則a=b，大家覺得這一判斷對嗎？

設計意圖：學生前面思維出現障礙，如果我們直接灌輸正確的結果可能印象不深，下次還是會錯，怎么辦？借助于追問4，學生在分析：如果a2=b2，有a=b或a=-b兩種情況時，很自然地就會發現前面的說法“方程（1）兩邊同時開方可以得到方程（2）”是有問題的.

追問5：那么應該怎么說呢？若a=b，則有a2=b2，這樣說對嗎？

學生有了上述思考，對于如何解無理方程就清晰了：將方程兩邊平方，將其轉化成有理方程再求解.

三、實踐體悟，引導在應用中感悟

數學概念的學習離不開應用過程，應用的過程是實踐，是進一步培養和發展的過程，前面對概念的理解程度和思維狀態都會在概念應用的過程中暴露出來，并有新的感悟.

1.設置例題，感悟方法

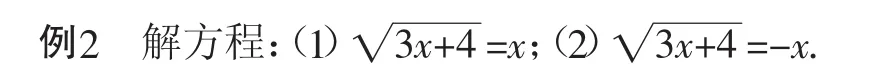
設計意圖：例2給出的是兩個不同的方程，但是最終的根是一樣的，自然地將思維轉向：這里面有怎樣的關聯呢？促進學生進一步比較與思考，很快在觀察與比較中感悟到方程的非同解變形會使方程根的范圍擴大，此時怎么辦？很自然地生成驗根的需要，這恰恰也是我們教學的重點、難點所在.

2.自主練習，比較“通法”和“巧法”

我們在數學教學的過程中，要謹防學生出現思維定式，同時要注意對學生發散性思維的引導，對于解無理方程而言，我們通常的方法是“平方法”，這樣的通法在教學中當然要練習和鞏固，但不要將“平方法”作為唯一路徑，要滲透巧法，讓學生的思維品質獲得有效提升.

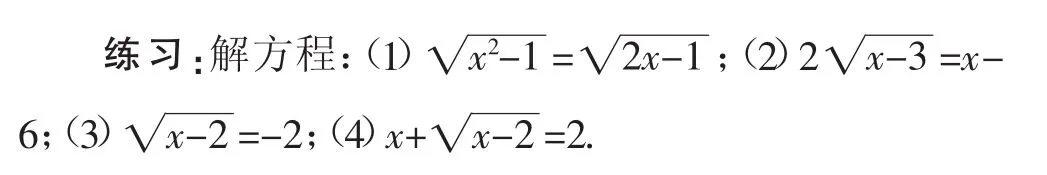
設計意圖：上述四個方程，學生借助于平方法很快可以解決，從學生完成的情況看，我們要提醒學生對于第（2）小題，不能把“2”的平方疏忽掉；在解決（3）、（4）兩個特殊的無理方程時，學生如果進行簡單的平方就容易出現問題，學生在自主嘗試并解決問題后，對解決無理方程的方法會有新的感悟，這是我們幫助學生有效克服思維定式負遷移的最好辦法.

四、總結歸納，引導學生在聯想中關聯

知識之間是有聯系的，我們每學習一個概念和方法，都應該引導學生將其歸納到原有的認知結構之中，在聯想中關聯，促進數學知識結構的建構式發展.

1.類比分析化歸思想

這節課的學習，我們可以引導學生總結，得出結論，如圖1所示.

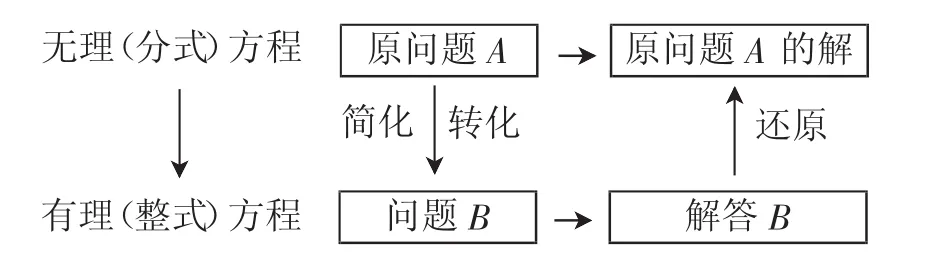
圖1

2.引導學生在“方程”和“式”的比較中感悟知識內在關聯，比較中得出方程的知識結構.

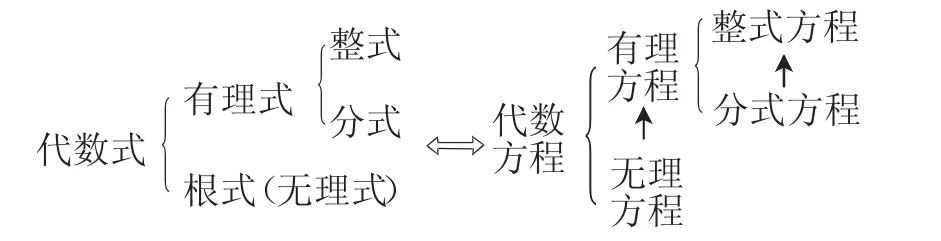
圖2

教育家馬登曾經發表過學習就是鑒別的著名觀點，鑒別又必須建立在比較的基礎之上，學習者自身必須具備一定的認知，才能從物質的、文化的、感知的世界中對某些特征進行辨認和察覺.筆者認為，初中數學教學，就應該讓學生在原有認知的基礎上進行“比較”，這是發展學生認知和實踐意識，提高學生解決實際問題能力的不二法門.