潛心分析學生能力基礎 精準把控數學課堂教學
陳 杰 姜海宏
(江蘇省南京市南湖第一小學,江蘇南京 210017 )
引 言
美國心理學家奧蘇伯爾認為,知識的掌握過程可以看成是通過一系列的心智活動,在頭腦中建立起相應的認知結構的過程[1]。筆者認為,隨著學習者年齡的增長和知識獲取渠道的增加,知識如何真正被學習者掌握并且形成技能,是一線教師必須關注的問題。教師不能把知識直接灌輸給學生,學生掌握知識必須要經歷一系列建構的過程。
一、學生的領會
“領會”是指領悟了事物中蘊含的道理并對其深有體會。領會是建立在對某一特定事物進行深入思考與悉心體悟的基礎上的。考慮到不同學習材料的難易程度,教師要尋找到切入點,選擇正確的教法,幫助學生更好地完成建構。
(一)知識聯結
在本環節中,學生接受新知識的刺激,自主激活相聯結的知識,用已有的知識去“同化”新的知識。如果學生在學習新知識的時候有困難,聽不懂教師的講解,我們就需要“借力打力”,準備一個和新知識相關聯的情境,讓學生按照一定的邏輯層次完成自我建構。
【案例一】
教學內容:蘇教版四年級下冊第十三單元《用字母表示數》
教師在開展這節課之前,考慮到班級里有幾個喜歡鉆牛角尖的學生,所以提前和家長打了招呼,讓他們幫孩子預習,從家長的反饋情況來看,大部分孩子的預習效果是比較令人滿意的。但是有一位父親的苦惱,讓筆者感覺有點不安……
“陳老師您好!我是王某的爸爸,我女兒始終搞不清a到底是多少,我和她說a就是a,表示多少都可以,她問我‘擺一個三角形用a根小棒行不行’,預習輔導我無法完成。”
之后筆者再次檢查自己的教案,這節課的流程是按照“用字母表示數—用字母表示數量—用字母表示公式”的教學思路進行的,很多教師都是按照這樣的方法來教的,這個學生連最簡單的環節“用字母表示數”都不能理解,下面的兩個層次該怎么進行啊?這樣的問題還真沒有遇到。
為什么其他的學生能理解,這個學生不能理解呢?原因是什么?筆者在課前問了學生,他們說在幼兒園的時候都學過一首兒歌,那么是不是這個王某沒有學過呢?抱著這樣的疑問,筆者問了她,她回答說沒有上過幼兒園。于是,筆者在上課的時候又把那首兒歌和學生一起念了一遍,他們明白了“多1只青蛙就多4條腿,多2只青蛙就多2個4條腿”,現在看來,這對新知識的理解起著關鍵作用。
筆者用這樣的例子只是想表達成人認為理所應當的事情,在孩子那里也許是難題,而成人往往會把原因歸結為孩子很“笨”,其實是孩子的腦海中沒有相聯結的經驗。
在信息爆炸的時代,很多信息是通過幼兒園教學以及通過電視、網絡傳遞給學生的,這樣的信息被教師誤認為是學生“已有的知識”,這對于那部分沒有接觸過現代信息的學生(尤其是留守兒童)是很不公平的。因此,教師需要多關注學生,了解他們的差異,這樣才能做到因材施教。
(二)信息加工
在本環節中,學生分析新舊知識之間的聯系,打通新舊知識的節點,形成知識組塊,由若干個元素按照一定的關系組成為一個整體完成刺激,形成新的知識,并且使新知識和更多的知識產生聯系。
【案例二】
教學內容:蘇教版五年級上冊第二單元《平行四邊形的面積》片段。
師:你能把圖中(如圖1所示)的平行四邊形轉化成長方形嗎?
生:能。
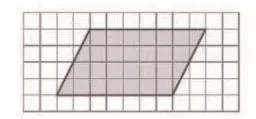
圖1
師:請拿出你準備好的1號圖形、剪刀,動手試一試。誰愿意把自己的想法和大家分享?請帶著你的作品到前面來,你剛才是怎樣剪的?(學生用手比畫,沿著角向下剪。)
師:剪一刀后變成什么圖形?
生:一個直角三角形和一個直角梯形。
師:你做得真棒!還有沒有其他的方法啊?你是怎樣剪的?你剪一刀之后變成什么圖形?剛才咱們在把平行四邊形轉化成長方形的時候,都是沿著什么剪的啊?
生:平行四邊形的一條高。
師:那我們為什么要沿著高剪呢?
生:能得到直角。
師:很好,還有誰想說……(引導過程省略)不錯,沿著高剪,拼成長方形的長就是平行四邊形的底,寬就是平行四邊形的高,這一個平行四邊形是這樣的,那么是不是所有的平行四邊形都是這樣的……
本節課的重點在于通過“剪、拼”將平行四邊形轉化成長方形,再通過觀察、數小格的方式完成對“平行四邊形的底→長方形的長,平行四邊形的高→長方形的寬”的加工,實現難點突破。在學生完成對材料加工的過程中,教師應重點考慮從學生的生活環境中挖掘有用的材料,通過這些材料來啟發學生來開展“同化”活動。特別要說明的是,有的知識是通過“同化”實現加工的,還有一些知識是通過“順應”實現加工的。
二、知識的鞏固
(一)陳述性知識
學習陳述性知識,學習者常用的方法是識記。識記指的是新知識在頭腦中留下痕跡的過程,體現在課堂教學中,教師需要將書本中的內容按照一定的方式呈現,幫助學生完成對新知識的接受。筆者以為,學生在對知識領會的過程中已經經歷了聯結和加工兩個環節,實際上已經完成了初步識記,但是因為他們的智力等因素,必定會在一定程度上形成差距,想要縮短差距,需要通過學生集中注意力來完成。
(二)程序性知識
學習程序性知識,學習者常用的方法是操作。當學生遇到某一個比較復雜的知識點的時候,教師往往會選擇動手操作的方法來幫助學生學習,但是學生通過操作活動所獲得的僅僅是直觀感覺,借助于手、眼等器官來發現,形成表象。
無論是陳述性知識還是程序性知識,隨著學習材料難度的增加,學生要對所學的內容進行復習、訓練、建模,當知識被回憶起來之后,再去完成相對應的鞏固作業,就會形成科學的學習方法,達成高效的學習效率。
三、知識的應用
在本環節中,主要是通過問題解決活動,建立新學會的數學知識和相關數學知識之間的廣泛聯系,構建知識的網絡,并在這個基礎之上形成相應的數學技能和數學解題策略,進而獲得結構功能良好的數學認知結構。對所學知識的靈活運用程度因人而異,但變式練習保持了知識的本質屬性不變而改變無關屬性,萬變不離其宗。知識的運用尤其是拓展,不可能一蹴而就,需要在學習的過程中對所學知識做詳細的分化。
結 語
通過本文的幾個案例可以了解,教師在教授新知的時候,對于易錯點要特別指出,避免學生出現較大的差錯率。因此,教師在設計課堂教案時應從學生的實際理解水平出發,不斷改進教育教學方法,同時要有意識、有針對性地幫助學生突破數學學習中的“攔路虎”。

