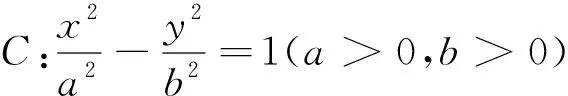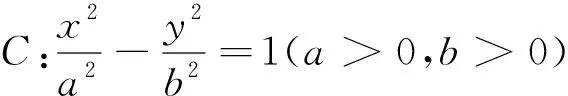圓錐曲線題中的等角問題

山東省聊城大學數學科學學院 (252000)

張 鑫 于興江

新課標全國Ⅰ卷的圓錐曲線部分難度變化不大，但穩中有變.本文以文科卷第20題及理科卷第19題為例，利用幾何畫板探究了直線與圓錐曲線相交時的等角問題.

2018年全國高考(文)Ⅰ卷第20題：設拋物線C:y2=2x，點A(2,0),B(-2,0)，過點A的直線l與C交于M，N兩點.

(1)設l與x軸垂直時，求直線BM的方程；

(2)證明：∠ABM=∠ABN.

(1)設l與x軸垂直時，求直線BM的方程；

(2)設O為坐標原點，則∠OMA=∠OMB.

我們利用幾何畫板探究得到.

定理1 設拋物線C:y2=2px(p>0)，點A(m,0),B(-m,0),m>0,過點A的直線l與C交于M,N兩點，則∠ABM=∠ABN.

圖1

證明:當l與x軸垂直時，AB為MN的垂直平分線，所以∠ABM=∠ABN.當l與x軸不垂直時，設l的方程為y=k(x-m)(k≠0),M(x1,y1),N(x2,y2),則x1>0,x2>0.

綜上所述，∠ABM=∠ABN.

注：2018年全國Ⅰ卷文科卷第20題中，當p=1,m=2時，經過點A的直線l與拋物線C交于M,N兩點，則∠ABM=∠ABN.

圖2

當l與x軸重合時，∠OMA=∠OMB=0°.

當l與x軸垂直時，OM為AB的垂直平分線，所以∠OMA=∠OMB.

當l與x軸既不重合也不垂直時，設l方程為y=k(x-c)(k≠0),A(x1,y1),B(x2,y2),則-a

將直線方程與橢圓方程聯立,得

將y1=k(x1-c),y2=k(x2-c)及x1+x2,x1x2的表達式代入(1)式中分子，可得

綜上所述，OMA=∠OMB.

注：2018年全國Ⅰ卷理科卷第19題中，當a2=2,b2=1時，經過右焦點F的直線l與橢圓C交于A,B兩點，點M的坐標為(2,0)，設O為坐標原點，則∠OMA=∠OMB.

圖3

當l與x軸重合時，∠OMA=∠OMB=180°.

當l與x軸垂直時，OM為AB的垂直平分線，所以OMA=∠OMB.

當l與x軸既不重合也不垂直時，設l的方程為y=k(x-c)(k≠0),A(x1,y1),B(x2,y2),則x1>a,x2>a.

將直線方程與雙曲線方程聯立

將y1=k(x1-c),y2=k(x2-c)及x1+x2,

綜上所述，OMA=∠OMB.

圖4

本文以探究圓錐曲線中等角問題為例，力求培養學生的創新意識及探索新知能力.